5. Ряды динамики

Ряды динамики характеризуют изменение уровней показателя во времени. Ряды динамики подразделяют на ряды динамики абсолютных, средних и относительных величин. По признаку времени ряды динамики абсолютных величин подразделяют на моментные и интервальные. Каждый ряд динамики состоит из двух элементов: периодов или моментов времени и уровней ряда.

Уровни ряда динамики должны быть сопоставимы по методологии расчета показателя, территории, продолжительности периодов времени, охватываемого объекта, единицам измерения и др. признакам.

В отдельных случаях для приведения уровней ряда к сопоставимому виду используется прием, который называют смыканием рядов динамики.

Пример 5.1. Имеются данные о поголовье крупного рогатого скота в районе (тыс. голов):

Таблица 5.1

№ п/п	Поголовье скота	Год
		2005	2006	2007	2008	2009	2010	2011
1	В старых границах	45,0	48,0	50,0	–	–	–	–
2	В новых границах	–	–	70,0	71,3	73,2	74,1	75,0
3	Сомкнутый ряд	63,0	67,2	70,0	71,3	73,2	74,1	75,0

Привести ряды к сопоставимому виду.

Решение: Определим коэффициент пересчета уровней в 2007 г., в котором произошло изменение границ района: К=70/50 = 1,4.

Умножая на этот коэффициент уровни ряда динамики в старых границах, приводим их к сопоставимым уровням в новых границах района: 2005 г. - ; 2006 г. -

Пример 5.2.

Таблица 5.2 – Среднемесячная заработная плата работников и стоимость набора из 25 основных продуктов питания

Месяц	Среднемесячная заработная плата, руб.	Стоимость набора из 25 основных продуктов питания, руб.
Январь	654,8	209,4
Февраль	684,4	216,6
Март	745,0	220,9
Апрель	746,5	224,1
Май	779,3	227,5
Июнь	837,2	232,5

Привести ряды динамики к одному основанию и сделать краткие выводы.

Решение: Для сравнения уровней рядов динамики необходимо привести их к одному основанию, т.е. исчислить базисные темпы роста.

Для среднемесячной заработной платы:

; и т.д.

Для стоимости набора продуктов питания:

; и т.д.

Представим полученные показатели в таблице:

Таблица 5.3 – Базисные темпы роста среднемесячной заработной платы и стоимости набора из 25 основных продуктов питания в РФ за 1 полугодие, %

Месяц	Среднемесячная заработная плата	Стоимость набора продуктов питания	Коэффициент опережения
Январь	100,0	100,0	–
Февраль	104,5	103,4	101
Март	113,8	105,5	108
Апрель	114,0	107,0	107
Май	119,0	108,6	110
Июнь	127,9	111,0	115

Данные таблицы показывают, что начисленная среднемесячная заработная плата на одного работника неуклонно растет. Стоимость набора из 25 основных продуктов питания тоже растет, но более медленными темпами.

В статистике для сравнения базисных темпов роста изучаемых рядов динамики за анализируемый период принято исчислять коэффициент опережения ( ) по формуле:

,

где – базисный темп первого ряда;

– базисный темп второго ряда.

Так для июня коэффициент опережения равен , или 115%.

Полученные данные представлены в таблице 5.3.

Коэффициенты опережения свидетельствуют о более высоких темпах роста заработной платы по сравнению с ростом цен на продукты питания.

В анализе динамики общественных явлений используется метод средних величин. Средний уровень ряда ( ) характеризует среднюю величину показателя за данный период. Средний уровень ряда рассчитывается как средняя величина из уровней ряда, для разных видов рядов динамики используется определенный метод расчета среднего уровня.

Пример 5.3. Имеются следующие данные о динамике производства продукции предприятием за 2007 – 2011 гг.:

Таблица 5.4

	2007	2008	2009	2010	2011
Объем произведенной продукции, млн. руб.	2040	2130	2220	2265	2360

Требуется определить среднегодовое производство продукции в 2007 – 2011 гг.

Решение: Для интервального ряда динамики средний уровень ( ) исчисляется по формуле средней арифметической простой:

,

где y – уровни ряда динамики;

n – число уровней ряда динамики.

млн. руб.

Пример 5.4. Имеются следующие данные об остатках сырья и материалов на складе предприятия:

Таблица 5.5

	1 января	1 февраля	1 марта	1 апреля
Остатки сырья и материалов на складе предприятия, млн. руб.	400	455	465	460

Определить среднемесячный остаток сырья и материалов на складе предприятия за I квартал.

Решение: по условию задачи имеется моментный ряд динамики с равными интервалами времени между датами учета, поэтому средний уровень ряда динамики будет исчислен по формуле средней хронологической:

млн.руб.

Пример 5.5. Имеются следующие данные о товарных запасах розничного торгового предприятия:

Таблица 5.6

	1.01	6.01	8.01	17.01
Товарные запасы торгового предприятия, тыс. руб.	1500	1530	1605	1630

Исчислить среднегодовой товарный запас розничного торгового предприятия.

Решение: Средний уровень товарных запасов за год для моментного ряда динамики с неравными интервалами исчислим по формуле средней хронологической взвешенной:

,

где у_i – уровени ряда,

t_i – период времени, в течение которого каждый уровень (y_i ) оставался неизменным.

Для анализа динамики общественных явлений в статистике применяются показатели динамики, которые рассчитываются двумя методами:

• цепной метод предполагает, что при расчете показателей динамики уровень каждого года сравнивается с предыдущим;

• базисный метод основан на том, что при расчете показателей динамики каждый уровень ряда сравнивается с одним, взятым за базу сравнения (чаще всего – начальным уровнем ряда).

К статистическим характеристикам динамического ряда относят показатели:

• абсолютный прирост;

• темп роста;

• темп прироста;

• абсолютное содержание одного процента прироста (методика расчета показателей динамики представлена в таблице 5.7).

Таблица 5.7

Показатели динамики	Цепной	Базисный
Абсолютный прирост
Темп роста
Темп прироста
Абсолютное содержание одного процента прироста

Пример 5.6. Имеются следующие данные о производстве продукции предприятия в 2006–2011 гг. (в сопоставимых ценах):

Таблица 5.8

	2006	2007	2008	2009	2010	2011
Объем производства, млн. руб.	80	84	89	95	101	108

Определить аналитические показатели ряда динамики производства продукции предприятия в 2008–2011 гг.

Решение:

1. Абсолютный прирост рассчитывается как разность между двумя уровнями ряда динамики:

• цепной:

; и т.д.

• базисный:

; и т.д. (табл. 5.9).

Таблица 5.9 – Абсолютные приросты объема производства продукции предприятием в 2006 – 2011 гг.

Год	Объем производства, млн. руб.	Абсолютный прирост ( ), млн. руб.
		Цепные (ежегодные)	Базисные (к 2006 г.)
2006	80	–	–
2007	84	4	4
2008	89	5	9
2009	95	6	15
2010	101	6	21
2011	108	7	28

2. Темп роста рассчитывается как разность между двумя уровнями ряда динамики и выражается в процентах или в коэффициентах:

• цепной:

;

и т.д.

• базисный:

; и т.д. (см. табл. 5.10).

Таблица 5.10 – Темпы роста объемов производства продукции предприятием в 2006 – 2011 гг.

Год	Объем производства млн. руб.	Темп тоста ( ), в %
		Цепные (ежегодные)	Базисные (к 2006 г.)
2006	80	–	–
2007	84	105,0	105,0
2008	89	106,0	111,2
2009	95	106,7	118,7
2010	101	106,3	126,2
2011	108	106.9	135,0

3. Темп прироста определяется как отношение цепного абсолютного прироста к предыдущему уровню (цепной) или отношение базисного абсолютного прироста к уровню ряда, принятому за базу сравнения:

• цепной:

; и т.д.

• базисный:

; и т.д. (табл. 5.11).

Между темпами роста и темпами прироста имеется взаимосвязь:

• , если темп роста выражен в процентах

• , если темп роста выражен в коэффициентах.

Таблица 5.11 – Темпы прироста объемов производства продукции предприятием в 2006 – 2011 гг.

Год	Объем производства млн. руб.	Темп прироста ( ), в %
		Цепные (ежегодные)	Базисные (к 2006 г.)
2006	80	–	–
2007	84	5,0	5,0
2008	89	6,0	11,2
2009	95	6,7	18,7
2010	101	6,3	26,2
2011	108	6,9	33,0

4. Абсолютное содержание одного процента прироста рассчитывается как отношение абсолютного прироста цепного к темпу прироста цепному:

и т.д. (табл. 5.12).

Таблица 5.12 – Абсолютное содержание одного процента прироста объемов производства продукции в 2006 – 2011 гг.

Год	Объем производства	Абсолютное содержание одного процента прироста ( ), тыс. руб.
2006	80	–
2007	84	800
2008	89	840
2009	95	890
2010	101	950
2011	108	1010

Средние показатели динамики:

1. средний абсолютный прирост исчисляется двумя способами:

• как средняя арифметическая простая из цепных приростов: , где n – число цепных абсолютных приростов;

• как отношение базисного прироста к числу периодов , где n – число уровней ряда динамики;

2. средний темп роста рассчитывается следующими способами:

• как средняя геометрическая из цепных темпов роста:

, где n – число цепных темпов роста;

• как корень n – ой степени из отношения последнего уровня ряда динамики к начальному (n – число уровней ряда динамики):

, где n – число уровней ряда динамики.

3. средний темп прироста исчисляется или .

При исследовании динамики общественных явлений анализу подвергается такое явление, как тенденция развития – основное направление динамики исследуемого социально–экономического явления.

Пример 5.7. Имеются следующие данные:

Таблица 5.13 – Потребление овощей в регионе в 2003–2011 гг. на одного человека домохозяйства в месяц. кг.:

	2003	2004	2005	2006	2007	2008	2009	2010	2011
Объем потребляемых овощей на 1 чел. в месяц, кг.	10,0	10,7	12.0	10,3	12,9	16,3	15,6	17,8	18,0

Необходимо выявить основную тенденцию потребления овощей в 2003–2011 гг.

Решение: В статистической практике применяются следующие методы выявления тенденции динамики общественных явлений:

1. метод скользящей средней;

2. метод укрупнения интервалов;

3. метод аналитического выравнивания.

Метод скользящей средней. Исчислим трехлетние скользящие средние уровни ряда за 2003–2005 гг.: кг.

за 2004–2006 гг.: кг. и т.д.

Результаты расчета трехлетней скользящей средней представлены в таблице 5.14.

Таблица 5.14 – Динамика потребления овощей на одного члена домохозяйства за месяц по региону в 2003–2001 гг., кг.

Год	Потребление овощей за месяц на одного члена домохозяйства ( )	Скользящие трехлетние суммы ( )	Трехлетние скользящие средние ( )
2003	10,0	–	–
2004	10,7	32,7 ( )	10,9
2005	12,0	33,0 ( )	11,0
2006	10,3	35,2 ( )	11,8
2007	12,9	39,5	13,2
2008	16,3	44,8	15,9
2009	15,6	49,7	16,6
2010	17,8	51,4 ( )	17,1
2011	18,0	–	–

В результате обработки ряда динамики методом скользящей средней проявилась тенденция к росту потребления овощей.

Метод укрупнения интервалов предполагает преобразование ряда динамики путем перехода от исходных периодов времени к более крупным.

Преобразуем ряд динамики, представленный в таблице 5.13, разбив его на три более крупных периода:

Таблица 5.15

Год	Потребление овощей за месяц на одного члена домохозяйства ( )	Периоды преобразованного ряда динамики	Расчетные уровни преобразованного ряда динамики ( )
2003	10,0	2003 – 2005
2004	10,7
2005	12,0
2006	10,3	2006 – 2008
2007	12,9
2008	16,3
2009	15,6	2009 – 2011
2010	17,8
2011	18,0

Метод аналитического выравнивания ряда динамики по прямой. Уравнение прямой имеет вид: ,

где – теоретические (расчетные) уровни ряда динамики;

и – параметры прямой;

t – показатель времени (дни, месяцы, годы и т.д.).

Для определения параметров уравнения и необходимо решить систему нормальных уравнений:

где – фактические уровни ряда динамики;

n – число уровней.

Для упрощения расчетов обозначим время таким образом, чтобы . В результате этого система нормальных уравнений примет вид:

Расчетные данные для определения параметров системы нормальных уравнений и выровненных теоретических значений:

Таблица 5.16

Год	Потребление овощей за месяц на одного члена домохозяйства ( )
2003	10,0	–4	16	–40,0
2004	10,7	–3	9	–32,1
2005	12,0	–2	4	–24,0
2006	10,3	–1	1	–10,3
2007	12,9	0	0	0
2008	16,3	1	1	16,3
2009	15,6	2	4	31,2
2010	17,8	3	9	53,4
2011	18,0	4	16	72,0

Отсюда: ;

Уравнение прямой (линейного тренда) будет иметь вид .

Теоретические (выровненные) уровни ряда динамики получаем подставляя в уравнение линейного тренда значения t:

Таблица 5.17

	2003	2004	2005	2006	2007	2008	2009	2010	2011
Выровненные значения ряда динамики,	9,30	10,41	11,52	12,63	13,74	14,85	15,96	17,07	18,18

Графическое изображение полученных данных называется линейным трендом:

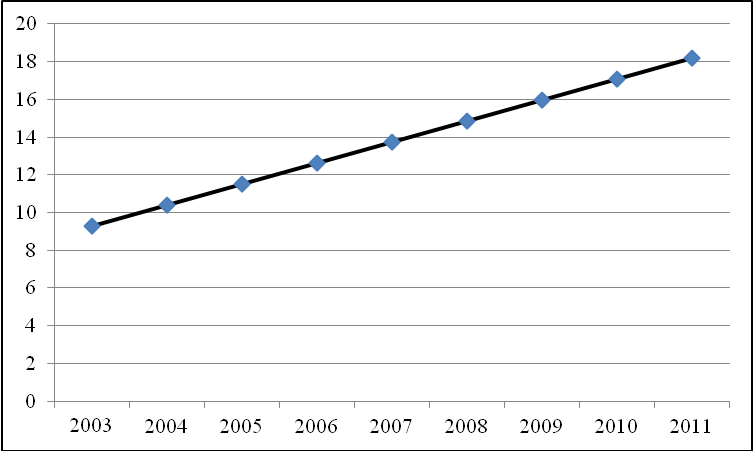
Рис. 5.1. Линейный тренд потребления овощей за месяц на одного члена домохозяйства, кг.

В динамике отдельных социально–экономических явлений имеют место периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку – сезонные колебания. Для их выявления и анализа в статистике применяют индексы сезонности. Для их исчисления применяют различные методы, выбор которых зависит от характера общей тенденции ряда динамики. Если ряд динамики не содержит ярко выраженной тенденции развития, то индексы сезонности исчисляют непосредственно по эмпирическим данным без их предварительного выравнивания. Для расчета индексов сезонности необходимо иметь данные об уровнях показателя в отдельные внутригодовые периоды (квартал, месяц) минимум за три года.

Индекс сезонности рассчитывается по следующей формуле:

,

где – среднемесячные (среднеквартальные) уровни ряда (по одноименным внутригодовым периодам);

– общий средний уровень ряда (общая средняя).

Пример 5.8. Реализация картофеля на рынках города за три года характеризуется следующими данными:

Таблица 5.18 – Объемы реализации картофеля на рынках города в 2009-2011 гг., т.

	Месяц
	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
2009	70	71	82	190	280	472	295	108	605	610	184	103
2010	71	85	84	308	383	443	261	84	630	450	177	168
2011	63	60	59	261	348	483	305	129	670	515	185	104

Определить индексы сезонности.

Решение: Для определения индексов сезонности рассчитаем средний уровень объема реализации для каждого месяца с помощью средней арифметической простой:

январь: т.;

февраль: т. и т.д. (табл. 5.19)

Рассчитаем общий средний уровень за три года:

т.

или т.

Реализация картофеля на рынках города за три года:

Таблица 5.19

Месяц	Реализация картофеля, т.
	2009 г.	2010 г.	2011 г.	Сумма за 3 года	Среднемесячный уровень за 3 года,
А	1	2	3	4	5
Январь	70	71	63	204	68
Февраль	71	85	60	216	72
Март	82	84	59	225	75
Апрель	190	308	261	759	253
Май	280	383	348	1011	337
Июнь	472	443	483	1398	466
Июль	295	261	305	861	287
Август	108	84	129	321	107
Сентябрь	605	630	670	1905	635

Продолжение таблицы 5.19

А	1	2	3	4	5
Октябрь	610	450	515	1575	525
Ноябрь	184	177	185	546	182
Декабрь	103	168	104	375	125
Итого:	3070	3144	3182	9396

Индексы сезонности имеют следующие значения:

январь: или 26,3 %;

февраль: или 27,6 % и т.д. (см. табл.)

Таблица 5.20. - Индексы сезонности реализации картофеля на рынках города в 2009–2011 гг.

Месяц	Индексы сезонности, %
А	1
Январь	26,3
Февраль	27,6
Март	28,7
Апрель	96,9
Май	129,1
Июнь	178,5
Июль		110,0
Август		41,0
Сентябрь		243,3
Октябрь		201,0
Ноябрь		69,7
Декабрь		47,9
Итого:		100,0

Для наглядности можно построить график сезонной волны реализации картофеля (рис. 5.2).

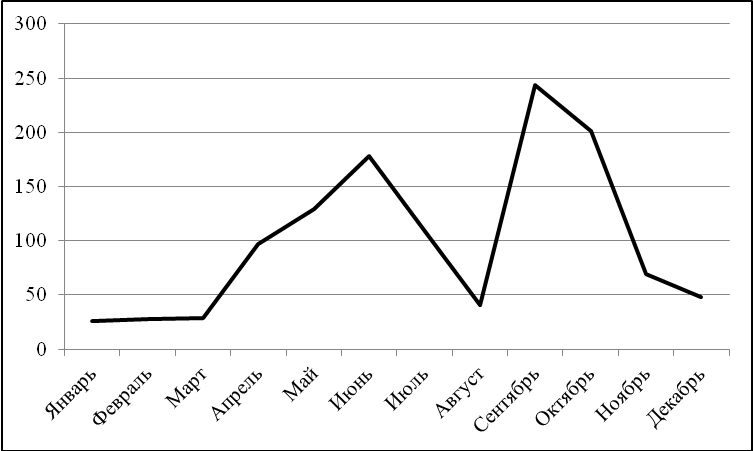
Рис. 5.2. Сезонная волна реализации картофеля

Пример 5.9. Имеются следующие данные о внутригодовой динамике заготовок сельскохозяйственной продукции в регионе по кварталам за три года:

Таблица 5.21 – Объемы заготовок сельскохозяйственной продукции в регионе

Квартал	Заготовлено продукции, тыс. руб.
	2009 год	2010 год	2011 год
I	162	159	158
II	170	193	225
III	177	178	187
IV	151	168	172

Для анализа внутригодовой динамики заготовок сельскохозяйственной продукции определить индексы сезонности.

Решение: Вычисление индексов сезонности в рядах динамики с тенденцией развития (к переменной средней).

Когда уровни ряда динамики проявляют тенденцию к росту или снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания. В таких случаях фактические данные сопоставляются с выравненными. Для расчета индекса сезонности в таких рядах динамики применяется формула:

,

где – теоретические (расчетные) уровни ряда;

– эмпирические (исходные) уровни ряда.

Определим теоретические значения ряда по уравнению: .

Для расчета параметров уравнения и составим таблицу:

Таблица 5.22

Квартал	Эмпирические уровни ряда
2009 год
I	162	–5,5	30,25	–891,0	162,6		99,6
II	170	–4,5	20,35	–765,0	164,8		103,2
III	177	–3,5	12,25	–619,5	167,1		195,9
IV	151	–2,5	6,25	–377,5	169,4		89,1
2010 год
I	159	–1,5	2,25	–238,5	171,6		92,7
II	193	0,5	0,25	–96,5	173,9		111,0
III	178	0,5	0,25	89,0	176,1		101,1
IV	168	1,5	2,20	252,0	178,4		94.2
2011 год
I	158	2,5	6,25	395,0		180,7	87,4
II	225	3,5	12,25	787,5		182.9	123,0
III	187	4,5	20,25	841,5		185,2	101,0
IV	172	5,5	30,25	946,0		187,3	91,8
							–

Отсюда: ; .

Следовательно, уравнение прямой будет иметь вид: .

Подставив в полученное уравнение значения t (квартальные), получим следующие выровненные значения ряда.

Для 2009 года:

I квартал:

II квартал:

III квартал:

IV квартал: и т.д. (см. табл.).

Рассчитаем процентные отношения эмпирических уровней ряда к теоретическим:

для 2009 года:

I квартал: ;

II квартал: и т.д.

Таблица 5.23

Квартал	2009 год	2010 год	2011 год
I	99,6	92,7	87,4
II	103,2	111,0	123,0
III	195,9	101,1	101,0
IV	89,1	94,2	91,8

Далее необходимо просуммировать полученные процентные отношения: за три года по одноименным кварталам:

I квартал:

II квартал:

III квартал:

IV квартал:

Вычислим индексы сезонности:

I квартал:

II квартал:

III квартал:

IV квартал:

Наибольший удельный вес заготовок сельскохозяйственной продукции приходится на второй квартал.