18. Теорема сложения вероятностей.

Теорема сложения вероятностей. Вероятность суммы двух несовместных событий и 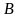равна сумме их вероятностей, то есть

(1)

Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице.

Следствие 2. Сумма вероятностей противоположных событий равна единице:

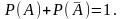
Предположим, что события и совместны. Тогда вероятность их суммы выражается формулой

(2)

то есть вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения (совместного наступления).

Заметим, что формула (1) является частным случаем формулы (2), ибо в случае несовместности событий и событие — невозможное и

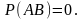
Два события являются независимыми, если вероятность одного из них не зависит от наступления или не наступления другого. Если же вероятность одного события меняется в зависимости от того, произошло другое событие или нет, то эти события являются зависимыми. В случае зависимых событий имеет смысл говорить об условной вероятности.

Вероятность события 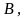  вычисленная при условии, что имело место другое событие  называется условной вероятностью события и обозначается: 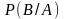или

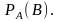
Аналогично определяется и обозначается условная вероятность события 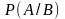или

19. Теорема умножения вероятностей.

Теорема умножения вероятностей. Вероятность произведения (совмещения) двух событий и равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое событие произошло, то есть

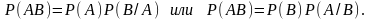(3)

Если события и являются независимыми, то по определению

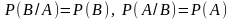
и формулы (3) примут вид

то есть вероятность совместного наступления двух независимых событий и равна произведению их вероятностей.

20. Повторные независимые испытания.

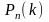Пусть производятся испытания, в каждом из которых может появиться событие . Если вероятность события в одном испытании не зависит от появления его в любом другом, то такие испытания называют независимыми относительно события  . Будем считать, что испытания происходят в одинаковых условиях, а вероятность появления события в каждом из них постоянна и равна Тогда вероятность того, что в серии из независимых испытаний событие произойдет раз (и не произойдет 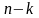раз), определяется по так называемой формуле Бернулли

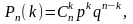21. (5)

где 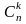— число сочетаний из элементов по 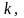— вероятность появления события в каждом испытании, — вероятность события 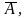противоположного событию

При малых значениях вероятность находится по формуле Бернулли (5) просто, однако при больших вычисления становятся громоздкими. Поэтому в последнем случае пользуются следующим утверждением, которое вытекает из локальной предельной теоремы Муавра-Лапласа: если при независимых испытаниях событие происходит с постоянной вероятностью которая не очень близка к нулю или единице ( ), то при достаточно большом числе испытаний вероятность того, что событие произойдет точно раз, приближенно равна

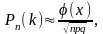(6)

где

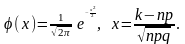
Формулу (6) называют локальной приближенной формулой Муавра-Лапласа.

Приближенное равенство (6) тем точнее, чем больше и чем ближе к 0,5. Имеются таблицы, в которых помещены значения функции соответствующие (см. приложение 1). Для отрицательных пользуются теми же таблицами, так как функция — четная ( ). При полагают

Локальная приближенная формула Муавра-Лапласа (6) дает возможность с небольшой погрешностью находить вероятность даже тогда, когда близко к нулю или единице при условии, что очень велико. В противном случае погрешность может оказаться значительной.

Французский математик Пуассон нашел другую формулу, по которой при малых значениях можно найти вероятность с небольшой погрешностью. Из предельной теоремы Пуассона следует: если при независимых испытаниях событие происходит с постоянной вероятностью близкой к нулю, то при достаточно большом числе испытаний вероятность осуществления события точно раз, приближенно равна

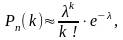(7)

где

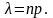
Формулу Пуассона (7) обычно применяют в тех случаях, когда 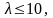а формулу Муавра-Лапласа (6) — при

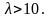
Формула Пуассона (7) используется также для расчета вероятности появления различного числа событий (точек) в какой-либо области (площади, объеме или во времени). При этом должны соблюдаться следующие условия:

а) точки в области распределены в общем равномерно;

б) положение каждой точки случайное, независимое друг от друга;

в) точки появляются в области по одиночке, а не парами, тройками и т. д.

Если соблюдены условия а), б), в) и указано среднее число появления точек на единицу области (площади, объеме, времени), то число 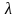точек, попадающих в область 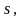внутри которой появляются интересующие нас события (точки), определяется произведением среднего числа и размера области то есть 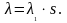В этом случае вероятность 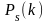появления событий (точек) в области 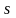определяется формулой Пуассона

(7^*)

где

Часто при решении задач требуется вычислить вероятность 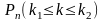того, что событие появится в независимых испытаниях не менее 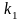и не более 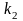раз. Эти задачи решаются с помощью теоремы сложения вероятностей и одной из формул: Бернулли, локальной приближенной формулы Муавра-Лапласа, Пуассона.

Действительно, вероятность того, что событие в независимых испытаниях наступит не менее и не более раз, будет равна вероятности наступления этого события или раз, или раз, … , или раз, то есть

(8)

Осталось вычислить вероятности, стоящие в правой части равенства (8) по одной из выше упомянутых формул и полученные результаты сложить.

В случае, когда число испытаний достаточно велико, а числа и значительно отличаются друг от друга, способ вычисления вероятности по формуле (8) будет громоздким. Эту проблему позволяет решить следующее утверждение, вытекающее из интегральной предельной теоремы Муавра-Лапласа: если в независимых испытаниях событие происходит с постоянной вероятностью которая отлична от 0 и 1, то при достаточно большом количестве испытаний вероятность того, что событие появится не менее и не более раз, приближенно равна

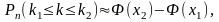(9)

где

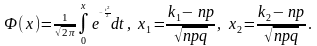
Формулу (9) называют интегральной приближенной формулой Муавра-Лапласа.

Обратим внимание на вид функции 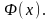Иногда у нее имеется множитель 2, то е 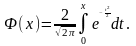В таких случаях в формуле (9) в правой части должен быть записан коэффициент 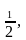 то есть

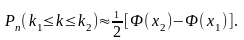
Функцию часто называют функцией Лапласа. Для нее составлены таблицы, соответствующие (см. приложение 2). При отрицательных пользуются теми же таблицами, так как 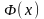— нечетная функция ( ). Для значений полагают