Повторение испытаний. Формула Бернулли. Наивероятнейшее число успехов.
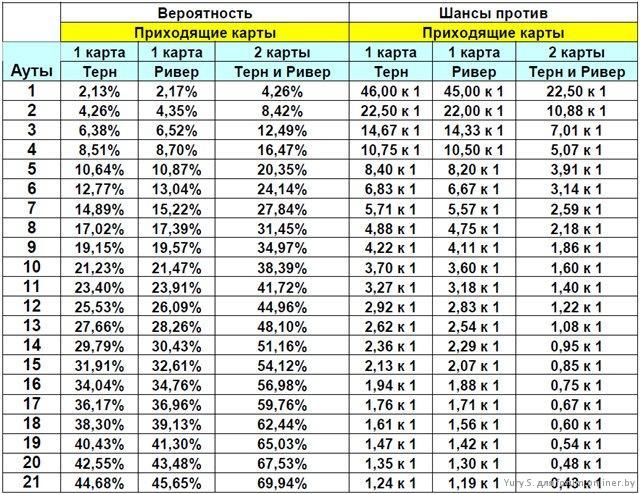
Ааххах! Шутка девчат!)))) Гыы!
Рассмотрим серию из п испытаний, в каждом из которых событие А появляется с одной и той же вероятностью р, причем результат каждого испытания не зависит от результатов остальных. Подобная постановка задачи называется схемой повторения испытаний. Найдем вероятность того, что в такой серии событие А произойдет ровно к раз (неважно, в какой последовательности). Интересующее нас событие представляет собой сумму равно-вероятных несовместных событий, заключающихся в том, что А произошло в некоторых к испытаниях и не произошло в остальных п — к испытаниях. Число таких событий равно числу сочетаний из п по к, то есть , а вероятность каждого из них: pkqn-k, где q = 1 — p — вероятность того, что в данном опыте А не произошло. Применяя теорему сложения для несовместных событий, получим формулу Бернулли:
Вывод
формулы Бернулли. Вероятность
одного сложного события, состоящего в
том, что в n
испытаниях событие A
наступит k
раз и не наступит n-k
раз, по теореме умножения вероятностей
независимых событий равна
.
Таких сложных событий может быть столько,
сколько можно составить сочетаний из
n
элементов по k
элементов, т. е.
. Так как эти сложные события несовместны,
то по теореме сложения вероятностей
несовместных событий искомая вероятность
равна сумме вероятностей всех возможных
сложных событий. Поскольку же вероятности
всех этих сложных событий одинаковы,
то искомая вероятность (появления раз
события A
в n
испытаниях) равна вероятности одного
сложного события, умноженной на их
число:
Или
Пример 4.1. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна p=0,75
Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна p=0,75.
Следовательно,
вероятность перерасхода электроэнергии
в каждые сутки также постоянна и равна
Искомая вероятность по формуле Бернулли равна
Повторение испытаний
Пусть производится при одних и тех же условиях n независимых испытаний, в каждом из которых вероятность появления некоторого события A постоянна и равна p, а непоявления q=1-p, то:
1.
Если
то имеет место формула Бернулли
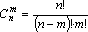
где
где
- наивероятнейшее число наступления
события A.
2.
а) Если n>10, 0<p<0,1, то имеет место
локальная теорема
Лапласа:
, где
,
а
значение
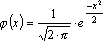
находится
по таблице, причем
б)
Интегральная теорема Лапласа
Масштабируйте девчат!!!)
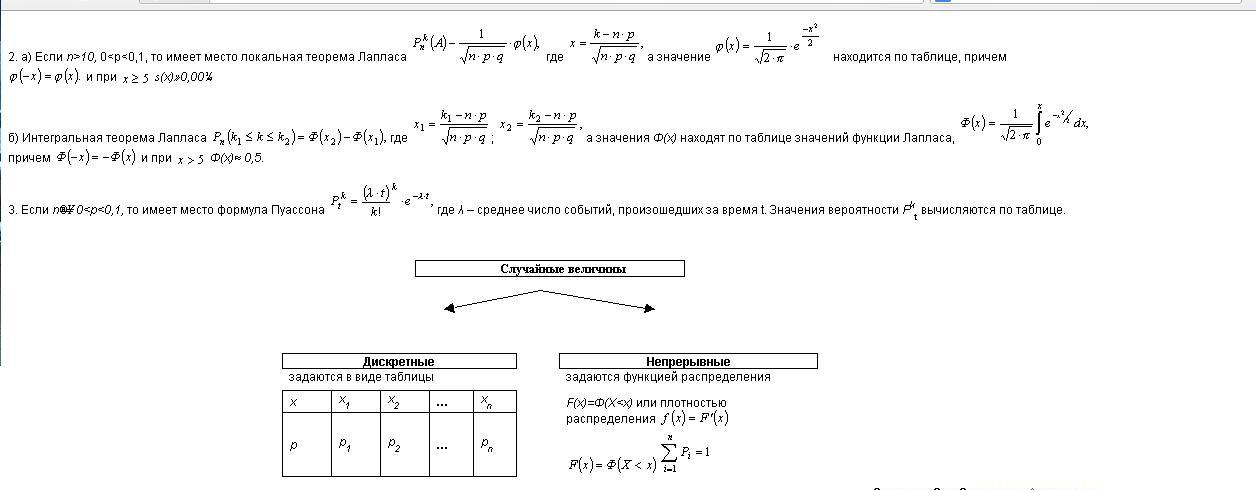
Как дано в тетрадке !
Формула Бернули. Если некоторое испытание повторяется практически в одинаковых условиях, несколько раз, в каждом отдельном испытании появляется или не появляется некоторое событие А, с постоянной вероятностью P(A) =p (вероятность успеха), тогда для нахождения вероятности события используется формула Бернули.
ДА ПОМОЖЕТ ВАМ БОГ ВОЛЖСКИХ ГВОЗДЕЙ!
А это я….
