Свойства вероятности. Вероятность суммы событий. Вероятность произведения событий. Независимость событий. Условная вероятность.
Свойства вероятности:
Свойство
1.
Вероятность невозможного события
равна 0, т.е.
Свойство 2. Вероятность достоверного события равна 1, т.е.
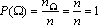
Свойство
3.
Для любого события
,
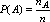т.к.
, то
,
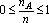и
следовательно
Свойство 4. Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей:
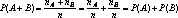
Свойство 5. (обобщенная теорема сложения вероятностей)
Свойство
6.
(теорема сложения k слагаемых) Если
события А1, А2,…, Аk попарно несовместимы,
то
Свойство
7.
Если
(А влечет В), то
,
тогда
Свойство
8.
Если
то
.
. Тогда
Свойство
9.
,
,
Свойство 10. Если события Н1, Н2,…,Нk образуют полную группу, то
.
Т.к
то по свойству 6:
http://www.coolreferat.com/Шпаргалка_по_Теории_Вероятности
Вероятность суммы событий.
Для
любых двух событий A и B справедливо:
Если
события A и B несовместны, то
Вероятность произведения событий. Независимость событий. Условная вероятность.
Условная вероятность P(A/B) события A при условии, что событие B произошло, P(B) > 0, определяется формулой
Для
любых двух событий A и B справедливо:
События
A и B называются независимыми,
если
Для
любых двух независимых,
событий A и B справедливо:
В гостях у математика….
Формула полной вероятности. Формула Байеса.
Пусть
A - произвольное событие, а события B1,
B2, …, Bn - попарно несовместны и образуют
полную группу событий, т.е.
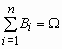
Тогда
имеет место следующая формула для
вероятности события A - формула
полной вероятности
-
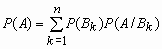
Как дано в тетрадке !
Пусть интересующее нас событие А может произойти или не произойти с 1 из ряда попарно несовместных событий H1, H2 … Hn, образующих полную группу. События такого рода – гипотезы. Их вероятности известны.
Т.е. P(A) H1, P(A) H2 … P(A) Hn.
Вероятность интересующего нас события А определяется из формулы полной вероятности:
P(A) = P(H1)* P H1 (A) +P(H2)* P H2 (A)…. + P(Hn)* P Hn (Hn)
ДАЛЕЕ! Паровозик тронулся чух-чух-чух… мозги осталися…. )
Если событие A произошло, то вероятность того, что имело место событие Bk
вычисляется по формуле Байеса:
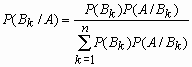
Как дано в тетрадке !
Формула Байеса: вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события:
P
A
(Hi) =
P(Hi)*
Hi(A)
/ P(A)
