Сочетание
Сочетание с повторением
Сочетание без повторения
Схемка
Вставить!
Формула включения — исключения
Определение. Число элементов множества A называется мощностью множества A и обозначается |A|.
Теорема.
Пусть даны множества
.
Тогда количество элементов в объединении
этих множеств можно найти по формуле:
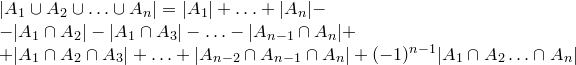
Доказательство проводится по индукции. Пусть n=2 . Нужно доказать формулу:
Действительно,
множество
состоит из всех элементов множества
A1
и тех элементов множества A2,
которые не содержатся в множестве A1.
Тогда, сложив количества элементов во
множествах A1
и A2,
мы два
раза посчитаем количество элементов, общих для множеств A1 и A2.
Предположим, что формула включения — исключения справедлива для n-1 множеств.
Докажем
ее для n
множеств. Множество
можно представить в виде
Тогда получаем (первое равенство по формуле включения — исключения для двух множеств):
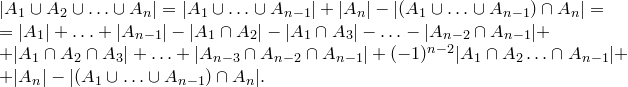
Используя формулу
и формулу включения — исключения для n-1 множеств, получаем
В эту формулу подставляем выражение, полученное ранее, и теорема доказана.
Элементы комбинаторики. Основные формулы комбинаторики. Число размещений с повторениями, число размещений без повторений, число перестановок из n элементов, число сочетаний без повторений.
Вставить схемку!
В данном разделе мы займёмся подсчётом числа «шансов». О числе шансов говорят, когда возможно несколько результатов какого-либо действия (извлечение карты из колоды, подбрасывание кубика или монетки). Число шансов — это число способов проделать это действие или, что то же самое, число возможных результатов этого действия.
Теорема о перемножении шансов
Пусть одно действие можно проделать пятью способами, а другое — двумя. Каким числом способов можно проделать пару этих действий?
Теорема
1.
Пусть
множество A
состоит
из k
элементов:
, а множество B
— из m
элементов:
.
Тогда можно образовать ровно km
пар , взяв первый элемент из множества
A,
а второй — из множества B.
Например: при подбрасывании трёх монет возможно 2·2·2=8 различных результатов;
Выбор без возвращения, с учётом порядка (размещение без повторения)
Теорема 2. Общее количество различных наборов при выборе k элементов из n без возвращения и с учётом порядка равняется:
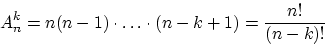
и называется числом размещений из n элементов по k элементов.
Следствие 1. Если в n множестве элементов, то существует ровно n! перестановок этих элементов.
Выбор без возвращения и без учёта порядка (cочетание без повторения)
Теорема 3. Общее количество различных наборов при выборе k элементов из n без возвращения и без учёта порядка равняется:
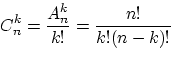
и называется числом сочетаний из n элементов по k элементов.
Выбор с возвращением и с учётом порядка
Теорема
4.
Общее количество различных наборов
при выборе k
элементов из n
с
возвращением и с учётом порядка равняется
Доказательство.
Первый шар можно выбрать n
способами. При каждом из этих способов
второй шар можно выбрать также n
способами,
и так k
раз. Общее число наборов равно
5. Выбор с возвращением и без учёта порядка
Теорема 5. Общее количество различных наборов при выборе k элементов из n с возвращением и без учёта порядка равняется:
Ыыыыыыыыыыыы! Как весело!
Классическое определение вероятности. Геометрическая вероятность. Задача о встрече.
Из тетрадки
Классическое определение вероятности:
Пусть в результате испытания произойдёт n простых попарно несовместных единств, возможных и равновозможных исходов, при которых интересующее нас событие A может произойти или не произойти (эти исходы образуют полную группу событий).
В m из этих исходов появление события А достоверно, в n-m исходах – невозможно (m<=n).
Исходы, при которых события А происходят обязательно, называются благоприятствующими появлению события A.
Вероятность события А – это отношение числа благоприятствующих этому событию исходов к общему числу всех простых попарно несовместимых единственно возможных и равновозможных исходов испытания. P(A) – вероятность к событию А.
P(A) = m/n
m=n - P(A)=1
m=0 - P(A)=0 – вероятность невозможного события
m<> (не равно)n - m <> (не равно) 0, - 0<P (A)<1
0<=P(A) <=1