8.5 Комбінаторні методи. Метод гілок та меж

В основі комбінаторних методів є перебір можливих варіантів розв’язків поставленої задачі. Кожен з них характеризується певною послідовністю перебору варіантів та правилами виключення, що дають змогу ще в процесі розв’язування задачі виявити неоптимальні варіанти без попередньої їх перевірки. Відносна ефективність різних методів залежить від того, наскільки кожен з них уможливлює скорочення необхідного процесу перебору варіантів у результаті застосування правила виключення.

Розглянемо один із комбінаторних методів. Для розв’язування задач цілочислового програмування ефективнішим за метод Гоморі є метод гілок і меж. Спочатку, як і в разі методу Гоморі, симплексним методом розв’язується послаблена (без умов цілочисловості) задача. Потім вводиться правило перебору.

Нехай потрібно знайти х_j – цілочислову змінну, значення якої х_j= в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Таким проміжком є інтервал між найближчими до цілочисловими значеннями. Можна стверджувати, що на інтервалі цілих значень немає.

Наприклад, якщо =2,7 дістаємо інтервал , де, очевидно, немає х_j, яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі , або . Виключення проміжку з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових нерів­ностей. Тобто допустиме ціле значення x_j має задовольняти одну з нерівностей виду:

або .

Дописавши кожну з цих умов до задачі з послабленими обмеженнями, дістанемо дві, не пов’язані між собою, задачі. Тобто, почат­кову задачу цілочислового програмування (7.1)-(7.4) поділимо на дві задачі з урахуванням умов цілочисловості змінних, значення яких в оптимальному плані послабленої задачі є дробовими. Це означає, що симплекс-методом розв’язуватимемо дві такі задачі:

перша задача:

(8.14)

за умов:

; (8.15)

; (8.16)

– цілі числа, ; (8.17)

, (8.18)

друга задача

(8.19)

за умов:

, ; (8.20)

; (8.21)

— цілі числа ; (8.22)

, (8.23)

де – дробова компонента розв’язку задачі (8.1)-(8.4).

Наведені задачі (8.14)-(8.18) і (8.19)-(8.23) спочатку послаб­люємо, тобто розв’язуємо з відкиданням обмежень (8.17) і (8.22). Якщо знайдені оптимальні плани задовольняють умови цілочисловості, то ці плани є розв’язками задачі (8.1)-(8.4). Інакше пошук розв’язку задачі триває. Для дальшого розгалуження вибираємо розв’язок задачі з більшим значенням цільової функції, якщо йдеться про максимізацію, і навпаки – з меншим значенням цільової функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не буде встановлено неможливість поліпшення розв’язку. Здобутий останній план – оптимальний.

Розв’язування цілочислових задач методом гілок і меж можна значно прискорити. Очевидно, що кожна наступна задача, яку отримують в процесі розв’язування відрізняється від попередньої лише одним обмеженням. Тому за послідовного розв’язування задач немає сенсу розв’язувати їх симплексним методом спочатку. Досить буде почергово приєднати нові обмеження виду (8.18) і (8.23) до останньої симплекс-таблиці попередньої задачі та вилучити (в разі необхідності) непотрібні «старі» обмеження.

Геометрично введення додаткових лінійних обмежень виду (8.18) та (8.23) в систему обмежень початкової задачі означає проведення гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих планів відповідної задачі лінійного програмування у такий спосіб, що уможливлюється включення в план найближчої цілої точки цього багатокутника (рис.8.4). Допустимо, що А – точка максимуму, тоді за методом гілок та меж багатокутник допустимих планів задачі ABCOD поділяється на дві частини прямими та +1, що виключає з розгляду точку А, координата якої є не цілим числом.

Рисунок 8.4

Опишемо алгоритм методу гілок та меж:

1. Симплексним методом розв’язують задачу (8.1)-(8.3) (без вимог цілочисловості змінних).

Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей розв’язок є оптимальним планом задачі цілочислового програмування (8.1)-(8.4).

Якщо задача (8.1)-(8.3) не має розв’язку (цільова функція необмежена, або система обмежень несумісна), то задача (8.1)-(8.4) також не має розв’язку.

2. Коли в умовно-оптимальному плані є дробові значення, то вибирають одну з нецілочислових змінних і визначають її цілу частину .

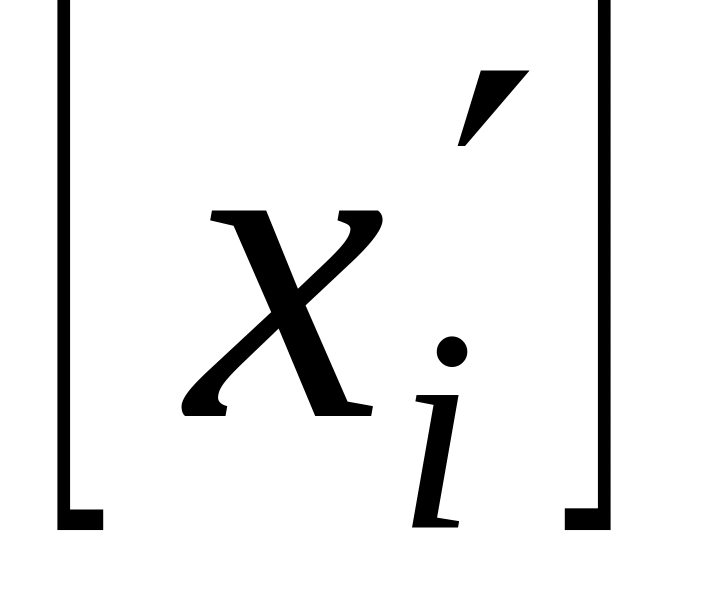3. Записують два обмеження, що відтинають нецілочислові розв’язки:

,

.

4. Кожну з одержаних нерівностей приєднують до обмежень початкової задачі. В результаті отримують дві нові цілочислові задачі лінійного програмування.

5. У будь-якій послідовності розв’язують обидві задачі. У разі, коли отримано цілочисловий розв’язок хоча б однієї із задач, значення цільової функції цієї задачі зіставляють з почат­ковим значенням. Якщо різниця не більша від заданого числа , то процес розв’язування може бути закінчено. У разі, коли цілочисловий розв’язок одержано в обох задачах, то з роз­в’язком початкової зіставляється той, який дає краще значення цільової функції. Якщо ж в обох задачах одержано нецілочислові розв’язки, то для дальшого гілкування вибирають ту задачу, для якої здобуто краще значення цільової функції і здійснюють перехід до кроку 2.

Приклад 8.2. Розв’яжемо методом гілок і меж задачу з прикладу 8.1.

Розв’язання. Відкинувши умову цілочисловості, дістанемо розв’язок: х₁=1, х₂= . Отже, допустиме ціле значення х₂ має задовольняти одну з нерівностей або . Приєднуємо до початкової задачі окремо кожне з обмежень, нехтуючи умовою цілочисловості, і розв’язуємо по черзі обидві утворені задачі:

Для задачі І (з обмеженням ) оптимальним буде розв’язок , , а для задачі IІ (з обмеженням ) – розв’язок , . Оскільки цілочислового плану не знайдено, процес необхідно продовжити, узявши для дальшого розгалуження першу задачу, оптимальний план якої дає більше значення функціонала. Розв’язуємо задачу І, окремо приєднуючи до неї обмеження: і . Отримуємо такі дві задачі:

Розв’язком задачі ІІІ є план , , а задачі IV – план , . Обидва розв’язки є цілочисловими, проте краще значення цільової функції забезпечує розв’язок задачі IV. Тому оптимальним планом початкової цілочислової задачі буде , , що збігається з розв’язком, отриманим за методом Гоморі.

Схема процесу розв’язування задачі з прикладу 8.1 (рис.8.5) досить наочно пояснює назву методу гілок та меж. Початкова задача розділяється (гілкується) на дві простіші, і, якщо серед них не існує задачі з цілочисловим оптимальним розв’язком, то процес гілкування продовжується. Отже, всі розглянуті дії можна зоб­разити у вигляді «дерева»:

Рисyнок 8.5

Кожен елемент такого «дерева» – це певна задача, що має відповідний оптимальний план. Після одержання нецілочислового розв’язку послабленої (тобто без умови цілочисловості) початкової задачі ми перетворили її на дві інші з додатковими умовами. З них кращим виявився розв’язок задачі І, однак оскільки він був не цілочисловим, то ми продовжили процес гілкування. Задачу І введенням додаткових обмежень перетворили в задачу ІІІ та задачу IV. Оптимальні плани обох цих задач цілочислові, але план задачі IV дає більше значення функціонала, тому цілочисловим оптимальним планом початкової задачі є розв’язок задачі IV.

Самостійна робота №8 – Приклади розв’язування задачі цілочислового лінійного програмування методом Гоморі та методом гілок і меж

Приклади розв’язку задачі цілочислового лінійного програмування методом Гоморі та методом гілок і меж [2, с.155-157], [3, с.159-160].

2. Вітлінський В.В., Наконечний С.І., Терещенко Т.О. Математичне програмування: Навчально-методичний посібник для самост. вивч.дисц. – 2-е вид., без змін. – К.: КНЕУ, 2006. – 248 c.

3. Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. – К.: КНЕУ, 2003. – 452 с.