
- •Интерполирование функции Конечные разности и их свойства.
- •Свойства конечных разностей
- •Связь конечных разностей и производных
- •Постановка задачи интерполирования функции
- •Первая интерполяционная формула Ньютона
- •Оценка точности интерполяционных формул
- •Численное интегрирование
- •Формула Симпсона (парабол)
- •Аппроксимация функции
- •Критерии согласия:
- •Метод наименьших квадратов
- •Основные свойства мнк:
Оценка точности интерполяционных формул
П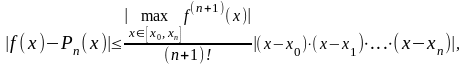 ри
интерполяции алгебраическими полиномами
n-го
порядка, по заданнымзначениям функции
f(x)
в (n+1)-ом
узле, находим многочлен Pn(x),
проходящий через эти точки. В этих
условиях имеет место неравенство:
ри
интерполяции алгебраическими полиномами
n-го
порядка, по заданнымзначениям функции
f(x)
в (n+1)-ом
узле, находим многочлен Pn(x),
проходящий через эти точки. В этих
условиях имеет место неравенство:
(4.14)
где f(n+1)(x) - (n+1)-ая производная функции f(x). Проанализируем формулу (4.14).
Слева стоит абсолютная разность между точным значением f(x) и его приближением Рn(x), т. е. абсолютная погрешность, а правая часть выражения (4.14) представляет оценку этой погрешности, т. е. предельную абсолютную погрешность. Неравенство (4.14) позволяет ответить на вопрос: от чего зависит точность интерполяции.
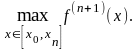
Начнем с множителя Как известно, значения производныхменьше для гладких функций с небольшими значениями grad(f(x)) и, наоборот, чем сильнее флуктуирует функция (значит большие значения grad(f(x))), тем больше и значения ее производных. Отсюда следует, что интерполяция точнее для более гладких функций.
Если с этой позиции посмотреть на геологические карты, то можно сказать следующее. Структурные карты более гладкие, особенно для условий Западной Сибири, по сравнению с картами эффективных нефтенасыщенных толщин hэн. Значит, при одном и том же числе измерений труктурная карта имеет более высокую точность чем карта hэн.
Далее, в знаменателе (4.14) стоит значение очень быстро растущей функции (n+1)!. Отсюда должно следовать, что с увеличением n, повышается и точность интерполяции. Но на практике это не выполняется. Дело в том, что неравенство (4.14) выведено без учета погрешностей измерений и конечныхразностей.
Как было показано ранее, с ростом n вычислительные погрешности конечных разностей растут очень быстро, и в геологической практике интерполяционные полиномы Рn(x) при n5 практически не используются.
Н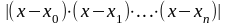 аконец,
рассмотрим последний сомножитель
формулы (4.14)
аконец,
рассмотрим последний сомножитель
формулы (4.14)
. Он представляет собой алгебраический полином (n+1)–го порядка с корнями х0, х1,…хn, обозначим этот полином wn+1(х). Схематично его поведение показано на рис. 2.
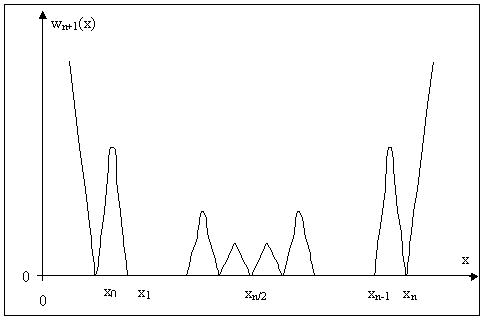
Рис.2. Схема изменения полинома wn+1(х)
Из геометрии wn+1(х) следует, что:
интерполяция имеет самую высокую точность в центре отрезка [x0, xn];
точность интерполяции ухудшается при движении интерполируемой
точки к краям отрезка [x0, xn];
экстраполяция всегда менее точна, чем интерполяция в узком смысле.
Численное интегрирование
Постановка задачи
Рассмотрим [a, b] и I =b∫aF(x)dx найти I по значениям F(xi), i=1, 2, … , n.
Формула трапеций
См рис в презент.
a∫bf(x)dx≈ [f(b)+f(a)]
[f(b)+f(a)]
R(f)=- f(ᶯ)
(a≤ᶯ≤b)
f(ᶯ)
(a≤ᶯ≤b)
Для повышения точности разобьем [а, b] на n равных отрезков с шагом и применим(6.1) к каждому отрезку [a+k·h, a+(k+1)·h]
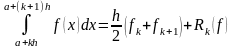 (6.3)
(6.3)

 (6.4)
(6.4)

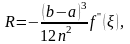 (6.5)
(6.5)
г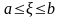 де
(6.6)
де
(6.6)
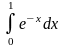
Пример. при n=4 и 8.

