Интерполирование функции Конечные разности и их свойства.
х х1 х2…хn
y y1 y2…yn (4.1)
П
усть
П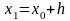
одробнее:
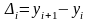
Определение. Выражение называют первой конечной разностью.
Если y=f(x):
(4.2)
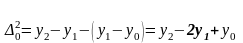
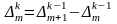
Свойства конечных разностей
1. Разностный оператор линеен:
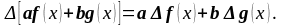(4.3)
П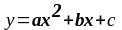
ример.
2
.
Таблица конечных разностей
-
х
у
Dу
D2у
D3у
х0
х1
х2
х3
у0
у1
у2
у3
Dу0
Dу1
Dу2
D2у0
D2у1
D3у0
Связь конечных разностей и производных
П
усть
y=f(x)
непрерывна и имеет непрерывные производные
до n-го
порядка включительно f(n)(x)
на отрезке [x,
x+n∆x],
тогда справедлива формула:
Постановка задачи интерполирования функции
Пусть на отрезке [a, b] заданы точки х0, х1,…,хn и известны значения функции f(x) в этих точках:
f(x0)=y0, f(x1)=y1,…, f(xn)=yn.
Требуется построить функцию F(x), принадлежащую известному классу R и принимающую в узлах интерполяции значения yi:
F(xi)=yi, i=0, 1,…,n. (4.1)
Функция f(x) называется интерполируемой, а F(x) – интерполирующей. Точки х0, х1,…,хn будем называть узлами интерполяции. Другими словами, задача интерполяции заключается в подборе графической или аналитической функции F(x) для таблично заданной f(x). Причем требуется, чтобы интерполируемая f(x) и интерполирующая функция F(x) совпадали в узлах интерполяции.
В приведенной постановке задача не корректна, а именно, имеет бесчисленное множество решений. Этот факт наглядно продемонстрирован на рис.(см.лекции)
На рис. приведены две различные кривые F1(x) и F2(x), удовлетворяющие условиям (4.1), т.е. являющиеся решением задачи интерполяции. Очевидно, что таких кривых можно начертить бесчисленное множество.Для некоторых классов функций R, например, классов алгебраических полиномов степени n - Pn(x), как будет показано ниже, задача интерполяции имеет единственное решение.
Далее будем различать два аспекта задачи интерполяции функций.
1. Пусть хp – точка, в которой вычисляется интерполирующее значение. Если точка хр принадлежит отрезку [x0, xn]: хpÎ[x0, xn], то задачу интерполяции называют интерполяцией в узком смысле.
2. Если точка хp не принадлежит отрезку [x0, xn], т.е. хpÏ[x0, xn], то задача называется экстраполяцией.
Эти аспекты в задаче интерполяции функций различаются в связи с тем, что экстраполяция всегда существенно менее точна, чем интерполяция в узком смысле. Этот важный момент более подробно будет рассмотрен ниже.