Глава 5

1. . 2. а) ; б) . 3. . 4. а) , б) , в) , г) . 5. 0,061.

6. а) . б)0, в) . г) . д) . 7. а) , б) , в) , г) . .8. , . 9.1) , 2) . 12. 99600. 14. 1) , 2) , 3) , 4) , 5) , 6) , 7) . 15. 3/4. 16. 2/ . 17. . 18 . 19. Решение. Обозначим через А событие «друзья встретились», а через x и y моменты прихода соответственно первого и второго из них. По условию x и y расположены между часами 13.00 и 14.00, то есть они могут меняться в течение часа. Значит, можно считать, что 0< x <1 и 0< y <1. Друзья встретятся, если время прихода одного из них отличается от времени прихода другого не более, чем на 30 минут, то есть если xy  /2.

Теперь для решения задачи необходимо изобразить на координатной плоскости область, определяемую неравенством xy  /2, и найти отношение площади полученной фигуры к площади квадрата, внутри которого она лежит.

Квадрат задается неравенствами 0< x <1 и 0< y <1.

20. 0,2. 21. а) А₁ А₂ А₃; б) ;

в) А₁ + А₂ + А₃+ А₁А₂ + А₁ А₃+ А₂ А₃ + А₁ А₂ А₃; г) А₂ А₃ + А₁ А₃ + А₁ А₂ ; д) А₂А₃ + А₁ А₃ + А₁ А₂ + А₁ А₂А₃; е) А_3.

Замечание: Если в пункте «в» событие С записать в виде: С= А₁ +А₂+ А₃, то при нахождении вероятности Р(С) надо учитывать совместность событий и считать Р(С) следующим образом:

Р(А₁ +А₂+ А₃) = Р(А₁ +А₂)+Р(А₃)  Р(А₁+А₂)Р(А₃) =

= Р(А₁ +А₂)(1Р(А₃))+ Р(А₃) =

( Р(А₁)+ Р(А₂)  Р(А₁) Р(А₂)) (1  Р(А₃))+ Р(А₃).

24. 0,8.

25. Р(А + В + С) = Р(А) + Р(В) + Р(С) = 0,15 + 0,1 + 0,12 = 0,37.

26. 0,4.

27. Р(А + В) = +  = .

28. 0,5.

29. Р(А + В) = .

30. Пусть А обозначает событие «У выбранного наудачу числа хотя бы две цифры совпадают». Тогда - это событие «у выбранного наудачу числа все цифры различны». Так как А + достоверное событие, то Р(А + ) = 1; с другой стороны, Р(А + ) = Р(А ) + Р( ), и следовательно, Р(А ) = 1  Р( ). Всего трехзначных чисел 900 (99999), количество трехзначных чисел, у которых все цифры различны, равно 9 9 8  648. Тогда Р( ) = = 0,72, и Р(А ) = 1  Р( ) = 1  0,72 = 0,28.

31. Р(АВ) = Р(А)Р(В) = 0,63.

32. 1) , 2) . 34. . 35. . 37. Р( ) =   = . Р(А ) =   = . 38. 40. 0,206; 0,988. 41. 1) 0,988;

2) 0,456; 3) 0,61; 4) 0,378; 5) 0,154. 42. + . Р(А) = Р(А₁ ) + Р( А₂). События А₁ и А₂ независимы, поэтому Р( ) + Р( ) , и следовательно, .

44. , . 45. . 48. . 50. 0,72; 0,54.

51. . 57. 0,77. 58. 0,003% . 59. 0,594. 60. 0,8667. 61. 0,024.

62. . 65. 0,325. 66. . 67. 0,038. 68. 17/52.

72. 5/11. 80. 1,9. 81. 1,5. 83.

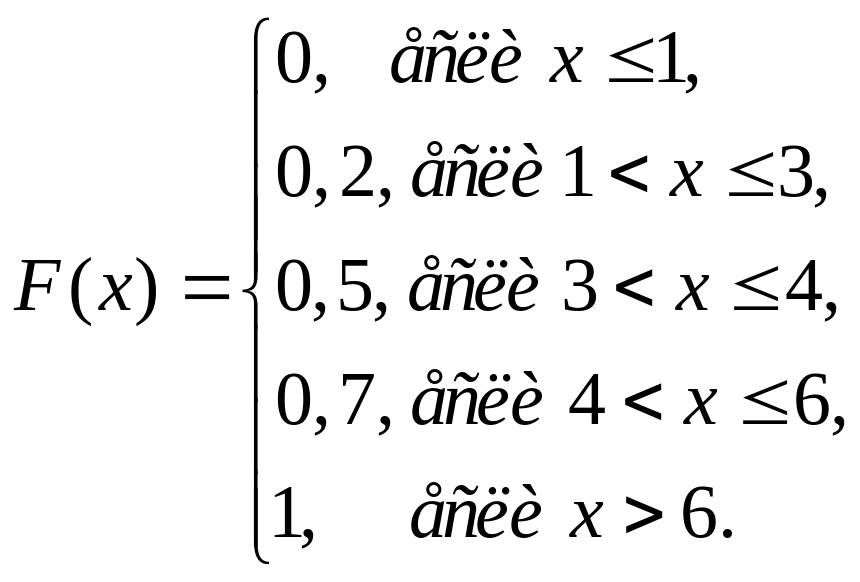
84. 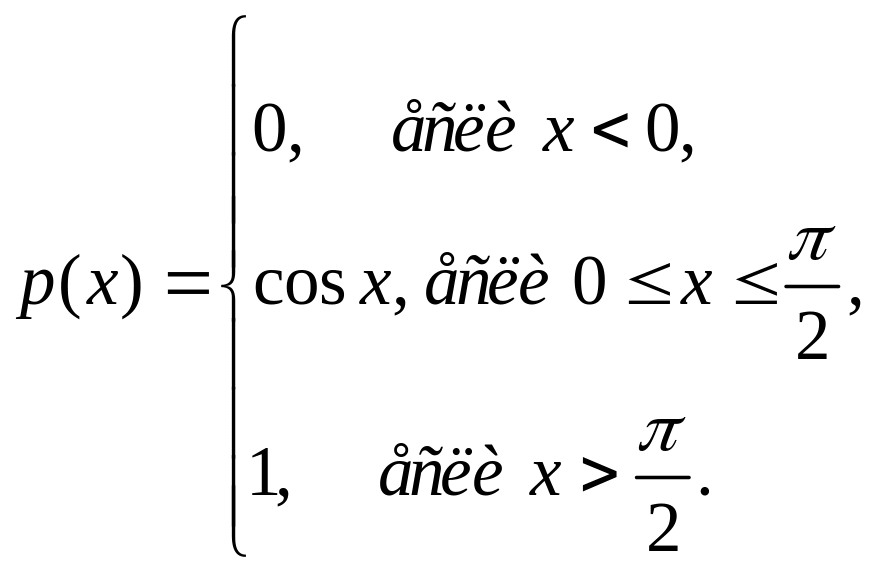85. 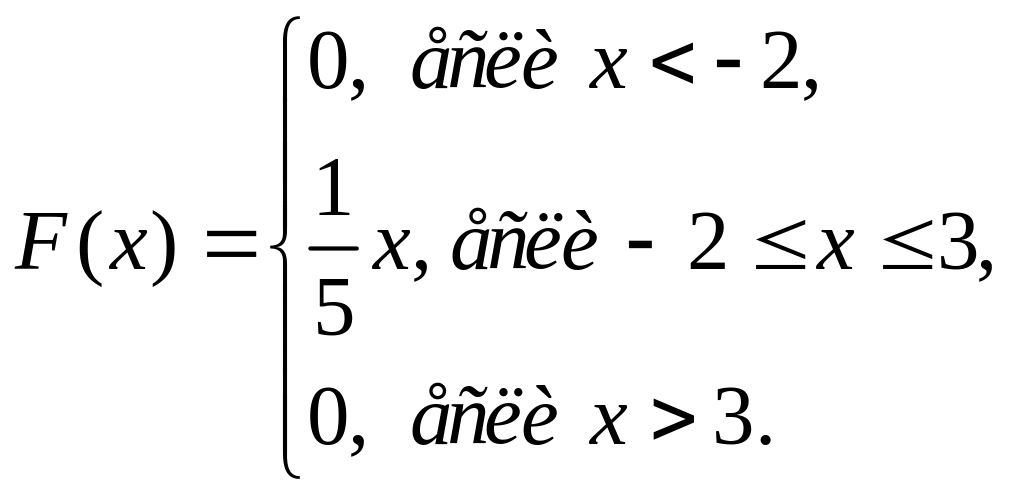86. 0,25.

87. 0,2. 88. 6 мин., 12 мин , 2 мин.

Глава 6

9. 4 . 11. 2621. 13. 5,1. 19 а) 7,63 < a < 12,77 . 19 b) 14,23 < a < 19,37.

20. 992, 16 < a < 1007,84. 21. . 23. .

27. . 29. а) , б) . 31. . 33. . 34. .

35. . 36. .