19.Метод Крамера решения систем

Решение систем методом Крамера

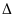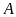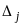Теорема Крамера. Пусть - определитель матрицы системы , а - определитель матрицы, получаемой из матрицы заменой столбца столбцом свободных членов. Тогда, если 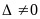, то система имеет единственное решение, определяемое по формулам: ( ).

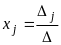Пример. Решить систему уравнений .

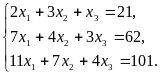Вычислим определители: , , , .

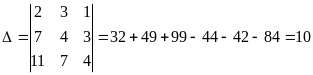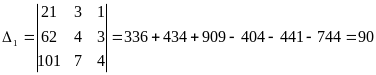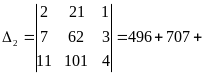
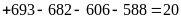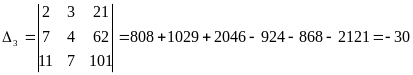Итак, , , .

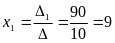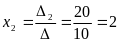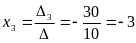20.Матричный метод решения систем

Решение систем матричным методом.

Этот способ или, как его еще называеют, метод обратной матрицы называется так потому, что все решение сводится к простому матричному уравнению, для решения которого необходимо найти обратную матрицу. Для того, что бы расставить все точки над и, рассмотрим метод под микроскопом.

Алгоритм решения достаточно просто. Как и в методах Гаусса и Крамера первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A^-1, получим A^-1AX= A^-1B, откуда EX=X=A^-1B. Следовательно, матрица-решение X легко находится как произведение A^-1 и B.

Для большей ясности решим небольшой пример методом обратной матрицы:

21x₁-45x₂-3.5x₃=10

12x₁-16x₂+21x₃=-16

14x₁+13x₂-8x₃=10

Определим совместность системы уравнений. По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, что быранг основной матрицы

 

A=	21 -45 3.5 12 -16 21 14 13 -8

 

и ранг расширенной матрицы

B=	21 -45 3.5 10 12 -16 21 -19 14 13 -8 10

 

были равны. Так как rang|A|=3 равен rang|B|=3 и равен количеству неизвестных n=3, то система имеет единственное решение.

Для решения методом обратной матрицы необходимо ввести матричные обозначения

 

A=

21 -45 3.5 12 -16 21 14 13 -8

X=

X1 X2 X3

C=

10 -19 10

, то X=A-1C

 

Найдем обратную матрицу A^-1. Как ее найти, показывать не будем. Воспользовавшись нашии онлайн калькулятором, вы сможете выбрать один из двух способов для ее нахождения. Она будет иметь вид.

 

A-1=	0.008 0.016 0.046 -0.02 0.011 0.021 -0.02 0.047 -0.011

 

Для нахождения матрицы X умножим обратную матрицу А^-1 на матрицу С

0.008 0.016 0.046 -0.02 0.011 0.021 -0.02 0.047 -0.011

10 -19 10

=

0.227 -0.209 -1.194

 

Получили решение системы уравнений X₁=0.227  X₂=-0.209  X₃=-1.194