2.3. Аналіз фактора часу при визначенні ефективності інвестиційних рішень

У фінансовій теорії під інвестиціями розуміють отримання реальних чи фінансових активів, тобто сьогоднішніх витрат, ме­тою яких є одержання прибутку в майбутньому. Якщо точніше, то інвестиції — цс обмін певної теперішньої вартості на майбут­ню, яка може бути і невизначеною.

Витрати і прибутки, пов'язані з будь-якою інвестицією, так чи інакше розподілені у часі. Завдяки тому, що в економіці водночас існує багато можливостей інвестування, ціна витрат і прибутку залежить від моменту часу, на який вони припада­ють. Саме тому вірна оцінка ефективності інвестицій немож­лива без правильного співставлення ціни цих витрат і прибут­ку за часом.

Для підтвердження цього основного принципу оцінки ефек­тивності інвестицій проаналізуємо приклад можливості інвесту­вання, яка при витратах 1 січня 1998 р. суми в 1 мли гри. прине­се 1 січня 1999 р. прибуток розміром 1,2 млн. грн. Для спрощення аналітичних розрахунків вважатимемо, що у даному випадку не­має жодного ризику, інфляція та оподаткування відсутні. Завдан­ня полягає у тому, щоб визначити, чи вигідний такий проект. Як­що немає ніяких альтернативних шляхів вкладання коштів, то він безумовно є вигідним. А якщо є можливість вкласти гроші, на­приклад, у банк, що приносить річний прибуток у розмірі d, то рішення буде залежати від величини d. Через рік цей капітал розміром 1 млн. грн., знаходячись на банківському депозиті, пере­твориться на величину 1(1+d) млн. грн. Якщо ж остання буде більшою за 1,2 млн. грн., то інвестиція буде невигідною, оскільки бан­ківський депозит принесе більший прибуток.

Існування альтернативної можливості інвестування, що забез­печує прибуток d на одиницю витрат, означає, що сьогоднішня сума в 1 млн. грн. через рік буде дорівнювати 1(1+d) млн. грн. Май­бутньою вартістю сьогоднішньої суми грошей Г_с називається ве­личина, що розраховується як

(2.23)

де d - максимально можливий прибуток у розрахунку на одиницю витрат, який можна отримати від альтернативних спо­собів інвестування за період часу, що розглядається; Г_с — сьогоднішня сума грошей.

Застосовуючи той самий принцип, можна визначити і вар­тість певної суми грошей, яку ми плануємо отримати чи витра­тній у майбутньому або сьогодні. Нинішньою вартістю майбут­нього грошового потоку Г_м називається величина

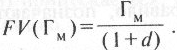(2.24)

Операцію розрахунку нинішньої вартості майбутнього гро­шового потоку називають дисконтуванням. Коефіцієнт, на який необхідно помножити майбутній грошовий потік, щоб отрима­ти його нинішню вартість, називають коефіцієнтом дисконту­вання.

Таким чином, оцінка ефективності фінансових вкладень по­лягає у порівнянні витрат і прибутку, зведених до одного мо­менту часу. Як правило, витрати і прибуток, що пов'язані з інве­стиційним проектом, зводять до сьогоднішнього моменту часу. У наведеному прикладі, якщо припустити, що d=10 %, то сьо­годнішня вартість прибутку у сумі 1,2 млн. грн. дорівнюватиме 1,091 млн. грн., що неважко перевірити:

При такому значенні d проект, що аналізується, є вигідним, оскільки нинішня вартість прибутку більша за нинішню вартість витрат (1,091 > 1).

Оцінка ефективності може проводитися й за іншим мето­дом. Назвемо прибутком інвестиційного проекту величину, що розраховується як

(2.25)

Величина d’ характеризує чисті вигоди, що приносить інве­стиційний проект у розрахунку на 1 гри. витрат. Доходність бан­ківського депозиту в нашому прикладі являє собою альтерна­тивні витрати інвестування. Якщо доходність проекту вища за альтернативні витрати (d’>d), то проект можна вважати вигід­ним і навпаки, якщо (d’<d).

Сформулюємо чіткіше визначення поняття нинішньої вар­тості майбутнього грошового потоку. Така вартість грошового потоку розміром С_м гри., що приходиться на визначений май­бутній момент часу, — це сума, яку необхідно інвестувати сьо­годні у найбільш прибутковий проект, щоб сумарний доход до певного майбутнього моменту часу складав величину С_м. Нинішню вартість, як правило, позначають функцією РV( ), майбутню вартість FV( ).

Розглянуті нами принципи співставлення витрат і доходів за часом дозволяють сформулювати чіткі правила оцінки ефектив­ності інвестицій. Отже інвестування вигідне, якщо сумарна дис­контована вартість доходів, яка забезпечується проектом, пере­вищує сумарну дисконтовану вартість витрат. Цей критерій має назву критерію чистої зведеної вартості (NPV).

Для наочності проаналізуємо інвестиційний проект, в яко­му передбачаються чисті грошові потоки С₀, С₁, С₂, ...С_п в момент часу t=0,1,2,..., n відповідно (момент 0 вважатимемо сьогоднішнім днем). Тоді грошовий потік в момент t визна­чається як

(2.26)

де ΔД — приріст доходів, пов'язаних з проектом;

ΔВ — приріст витрат.

Чистою зведеною вартістю інвестиційного проекту будемо називати сумарну нинішню вартість чистих грошових потоків, які забезпечують проект

(2.27)

Інакше, чиста зведена вартість — це сумарна зведена вар­тість за відрахуванням зведеної вартості витрат. Критерій NPV оцінки інвестиційних рішень полягає у порівнянні нинішньої вартості витрат і доходів: якщо NPV >0, то інвестування вигід­не, і навпаки, якщо NPV <0 — невигідне, якщо NPV=0, інвес­тування ані прибуткове, ані збиткове.

Якщо вважати, що грошові потоки Сt, розміщені через рівні проміжки часу, які дорівнюють одному року (тобто С1 виникає через рік, С₂ — через 2 роки і т. д.), то чисту зведену вартість слід розраховувати таким чином:

(2.28)

де d— максимальна доходність (процентів на рік), що забез­печується альтернативними способами вкладання коштів, при­чому в формулі (2.28) припускається, що величина d з плином часу лишається незмінною.

Наприклад, для проекту, що розглядався на початку цього розділу, С₀=-1 млн гри., С1=1,2 млн грн. Якщо d=10 %, то

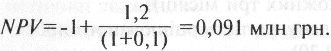
Якщо тривалість проміжків часу між грошовими потоками, що виникають у моменти (t—1) і t(t = 1,..,n) однакова, але мен­ша ніж рік (наприклад, т разів на рік), то чиста зведена вартість може бути розрахована за формулою

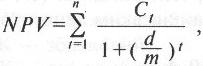(2.29)

де d — річна доходність альтернативних інвестицій з такою ж періодичністю виплат.

У загальному випадку для будь-якої неперіодичної послідов­ності грошових потоків чисту зведену вартість доцільно розра­ховувати за формулою

(2.30)

де w(t) — термін часу до моменту виникнення грошового по­току;

de — річна ефективна доходність альтернативних інвестицій.

Очевидно, що доходність альтернативних інвестиційних рі­шень може змінюватися з плином часу, а тому грошові потоки в загальному випадку повинні бути дисконтовані за ставкою, що відповідає моменту часу, в який вони виникають, а тому точні­шим варіантом формули (2.30) буде вираз

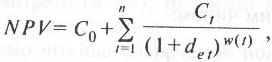(2.31)

де det — ефективна доходність альтернативних вкладень за період від сьогоднішнього дня до моменту виникнення t-го гро­шового потоку.

Розрахуємо чисту зведену вартість за певним інвестиційним проектом, який передбачає такі грошові потоки, грн.: С₀=-1000; С1 = 300 через 3 міс; С₂= 1000 через 9 міс. Як альтернативне ін­вестиційне рішення розглянемо банківський депозит, що забез­печує доходність у 40 % річних із поквартальною сплатою про­центів (10 % від суми вкладу кожних три місяці).

Тепер обчислимо чисту зведену вартість оцінюваного проек­ту, користуючись формулою (2.30)

тобто інвестиційний проект вигідний (NPV >0). Ефективна ставка за банківським депозитом у нашому при­кладі дорівнює

отже чиста зведена вартість відповідно до формули (2.31) бу­де такою:

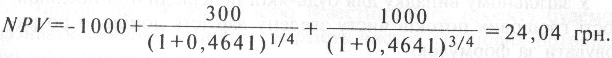
Для більш повної оцінки ефективності інвестицій продов­жимо аналіз впливу фактора часу на критерій внутрішньої нор­ми доходності. Внутрішньою нормою доходності (Internal Rate Return — ІRR) інвестиції називається таке значення станки дисконтування, за якої нинішня вартість витрат дорівнює ни­нішній вартості доходів, тобто таке значення величини d, коли NPV=f(d)=0.

Суть розрахунку цього коефіцієнта при аналізі ефектив­ності запланованих інвестицій полягає у такому. ІRR відобра­жає максимально допустимий відносний рівень витрат, які мо­жуть бути пов'язані з проектом. Наприклад, якщо проект повністю фінансується за рахунок позички комерційного бан­ку, то значення ІRR відображає верхню межу допустимого рів­ня банківської процентної ставки, перевищення якої робить проект збитковим.

На практиці будь-яке підприємство фінансує свою діяль­ність, у тому числі інвестиційну, з різних джерел. Як плату за користування авансованими у діяльність підприємства фінан­совими ресурсами воно сплачує проценти, дивіденди, винаго­роду тощо, тобто несе певні обґрунтовані витрати на підтри­мання свого економічного потенціалу. Показник, що характе­ризує відносний рівень цих витрат, можна назвати «ціною» авансованого капіталу (ЦК). Він відображає мінімальне повер­нення на вкладений у діяльність підприємства капітал та його рентабельність і розраховується за формулою середньої ариф­метичної зваженої.

Підприємство може приймати будь-які рішення інвес­тиційного характеру, рівень рентабельності яких не нижчий від поточного значення показника ЦК (або ціни джерела коштів для проекту). Саме з ним порівнюється показник ІRR, що роз­раховується для конкретного проекту. При цьому зв'язок між ними такий:

якщо ІRR > ЦК, то проект прибутковий;

ІRR < ЦК - збитковий;

ІRR = ЦК — ані прибутковий, ані збитковий.

Значення показника ІRR для інвестиційного проекту визна­чається методом послідовних ітерацій із використанням табульованих величин дисконтованих множників. Для цього за допомо­гою таблиць вибираються два значення коефіцієнта дисконту­вання d1<d2 таким чином, щоб в інтервалі (d1,d₂) функція

NPV=f(х) змінювала своє значення з «+» на «—» чи навпаки. Потім застосовують формулу

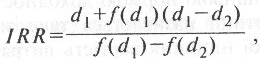(2.32)

де d1 — значення табульованого коефіцієнта дисконтування, за якого f(d1)<0;

d₂ — значення табульованого коефіцієнта дисконтування, за якого f(d₂)<0.

Точність розрахунків обернено пропорційна довжині інтер­валу (d1, d₂), а найкраща апроксимація із застосуванням табульованих значень досягається у випадку, коли довжина інтерва­лу мінімальна (дорівнює 1 %), тобто d1, і d₂ найближчі один до одного значення коефіцієнта дисконтування, що відповідають умовам (у випадку зміни знаку «+» на «—»):

d1 — значення табульованого коефіцієнта дисконтування, що мінімізує позитивне значення показника NPV, тобто f(d1)=mind {f(d)<0}

d₂ — значення табульованого коефіцієнта дисконтування, що максимізує від'ємне значення показника NPV, тобто f(d₂)=mind {f(d)<0}

Через взаємну заміну коефіцієнтів d1 і d₂ аналогічні умови застосовуються для ситуації, коли функція змінює знак з «—» на «+». '

Обчислимо IRR на конкретному прикладі: для проекту, роз­рахованого на 3 роки, що вимагає інвестицій розміром 10 млн. гри. і має передбачені грошові надходження розміром, млн. грн.: З, 4, 7.

Візьмемо два довільні значення коефіцієнта дисконтування d1 = 10%, d₂ = 20%.

Із застосуванням табульованих значень d1 і <d₂ визначимо

При подальшій зміні величин d1 і d₂ знайдемо найближчі цільові значення коефіцієнта дисконтування, при яких NPV змі­нює знак: при d1= 16% NPV = +0,05; при d₂=17% NPV=-0,14. Тоді уточнене значення IRR буде дорівнювати

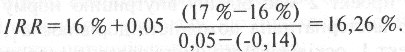
Отже дійсне значення IRR дорівнюватиме 16,26%.

Величина чистої зведеної вартості в більшості випадків обер­нено залежить від ставки дисконтування. Дійсно, чим більше значення d, тим менша нинішня вартість майбутніх доходів, то­ді як витрати, як правило, здійснюються у початкові періоди ре­алізації інвестиційного проекту. Значення d, для якого NPV=0, є внутрішньою нормою доходності проекту. У випадку, коли про­ект передбачає значні витрати наприкінці періоду реалізації, за­лежність чистої зведеної вартості від ставки дисконтування мо­же бути представлена як NРV=f(d)=0: при низьких значеннях d нинішня вартість майбутніх витрат велика, відповідно і про­ект невигідний; підвищення значення d робить величину NPV позитивною, але в подальшому при зростанні ставки дисконту­вання зведена вартість доходів вже не компенсує початкові ви­трати, а отже значення NPV стає від'ємним.

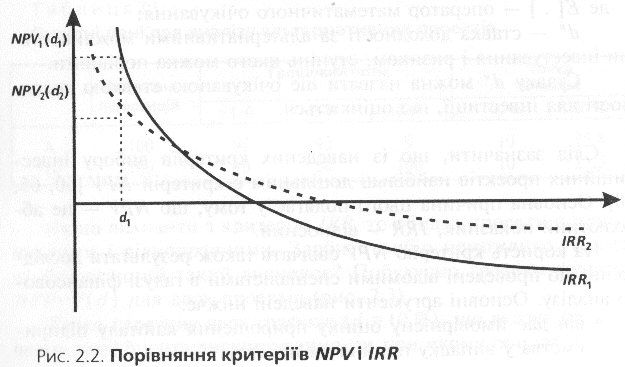
Обидва проаналізовані критерії оцінки ефективності інвес­тиційних рішень дають однаковий результат при вирішенні пи­тання щодо вигідності інвестицій. Проте кожен з них має свої особливості, і для будь-якої інвестиції завжди корисно розрахо­вувати обидва показники. Залежність NPV від ставки дисконту­вання для першого і другого проектів показана на графіку (рис. 2.2), одержаному при аналізі А. В. Мертенсом [86].

Як бачимо, проект 2 має більшу внутрішню норму доходності, але якщо альтернативна доходність дорівнює d1 то ви­гіднішим є проект 1, оскільки його чиста зведена вартість вища.

Коли йшлося про вартість грошей у часі, то вважали, що іс­нує абсолютна впевненість в одержанні майбутніх доходів на ін­вестовані кошти, оскільки є повна визначеність щодо альтерна­тивних можливостей інвестування, доходність яких використо­вувалася як ставка дисконтування. Але тут немає відповіді на питання, як оцінити нинішню вартість майбутніх грошових по­токів за відсутності визначеності стосовно їх розмірів. Відповідь може бути знайдена, якщо сформулювати правило таким чином: ставка дисконтування повинна відповідати ступеню впевненості інвестора в отриманні майбутнього доходу, тобто враховувати ступінь ризику, пов'язаного з інвестицією. Тому за ставку дис­контування має використовуватись доходність альтернативних рішень з таким самим чи подібним ступенем ризику. Для не­схильного до ризику інвестора можуть бути дві альтернативи щодо інвестування коштів — за умови повної визначеності та за наявності ризику. Вони будуть еквівалентними, якщо очікувана доходність ризикової інвестиції перевищує безризикову до­ходність на величину, що називається премією за ризик.

Таким чином, якщо С”M — випадкова величина майбутнього грошового потоку, то його нинішня вартість дорівнює

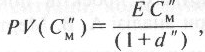(2.33)

де E[ . ] — оператор математичного очікування;

d" — ставка доходності за альтернативними можливостя­ми інвестування і ризиком, ступінь якого можна порівняти.

Ставку d" можна назвати ще очікуваною ставкою доход­ності для інвестиції, що оцінюється.

Слід зазначити, що із наведених критеріїв вибору інвес­тиційних проектів найбільш доцільним є критерій NPV [60, 65, 70|. Основна причина цього полягає у тому, що NPV — це аб­солютний показник, ІRR. — відносний.

На користь критерію NPV свідчать також результати дослід­жень, що проведені відомими спеціалістами в галузі фінансово­го аналізу. Основні аргументи наведені нижче:

• він дає ймовірнісну оцінку прирощення капіталу підпри­ємства у випадку прийняття проекту;

• критерій повною мірою відповідає основній меті діяльності керівного персоналу, що полягає у нарощуванні еконо­мічного потенціалу підприємства;

• йому притаманна пласти вість адитивності, що дає мож­ливість складати значення показника NPV за різними про­ектами і використовувати агреговану величину для оп-тимізації інвестиційного проекту.

Що ж до показника IRR, то він має ряд серйозних недоліків 110, ЗІ, 60|:

• оскільки це відносний показник, то за його допомогою неможливо дійти правильного висновку стосовно альтер­нативних проектів з позицій їх можливого внеску у збіль­шення капіталу підприємства, особливо коли проекти сут­тєво відрізняються один від одного за величиною грошо­вих потоків;

• критерій IRR показує лише максимальний рівень витрат, що може асоціюватися з оцінюваним проектом. Зокрема, якщо «ціна» інвестицій в обидва альтернативні проекти менша, ніж значення ІКР для них, то вибір може бути зроблений лише за допомогою додаткових критеріїв. До того ж критерій ІRR не дозволяє виявити ситуацію, коли «ціна» капіталу змінюється.

Для підтвердження розглянемо приклад. У табл. 2.1 наведені вихідні дані по двох альтернативних проектах. Необхідно вибра­ти один з них за умови, що «ціна» капіталу, призначеного для інвестування, дорівнює, %: а) 8; б) 15.

Якщо виходити з критерію ІRR, то обидва проекти є прий­нятними і рівноправними. Зробити вибір неможливо. Проте чи бездоганний такий висновок? Побудуємо графіки функції NPV=f(d) для двох проектів (рис. 2.3).

Точка перетину двох графіків (d = 10 %), що вказує на зна­чення коефіцієнта дисконтування, та при якому обидва проекти мають однаковий показник NPV , називається точкою Фіше­ра. Вона розрізнює ситуації, що визначаються критерієм NPV і не визначаються критерієм IRR.

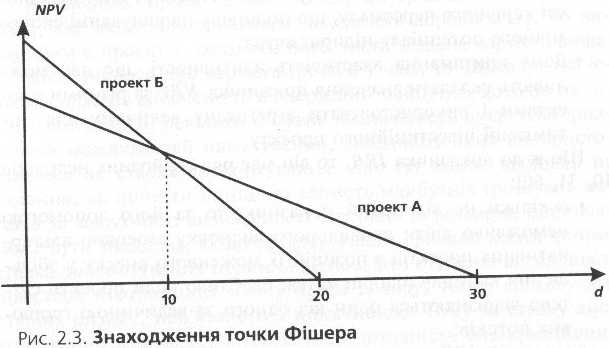
У наведеному прикладі критерій ІRR не може визначити пріоритети і не вказує на відмінність між ситуаціями а і б. Кри­терій NPV, навпаки, дає можливість визначити пріоритети за будь-якої ситуації. І він вказує на те, то ситуації а і б принци­пово відрізняються одна від одної, а саме: у випадку а слід прийняти проект А, оскільки він має більшу величину NPV; у випадку б перевага віддається проекту Б.

Суттєвим недоліком критерію ІRR є й те, що на відміну від критерію NPV йому не властива адитивність,