3.4. Порівняння і вибір ефективного варіанту реалізації інвестиційних проектів з різними термінами дії

При оцінці інвестиційних проектів, що мають тотожні харак­теристики, але різні строки дії, виникають певні ускладнення, по­в'язані з вибором серед них найбільш ефективного. Недоречно, наприклад, просто порівнювати різні за термінами проекти за по­казником NPV, оскільки нереально порівнювати 5-річний проект з 15-річним. З одного боку, короткострокові проекти вимагають частої заміни, а з іншого — завдяки їх короткостроковості можна вивільнити кошти для інвестування в інші об'єкти. Для зіставлен­ня ці проекти мають бути зведені до порівнянного вигляду. У між­народній практиці це робиться у такі способи.

1. Знаходиться найменше загальне кратне термінів дії про­ектів і передбачається, що проект з найкоротшим терміном дії самовідновлюється після свого завершення (тобто порівнюють­ся два 5-річні проекти з одним 10-річним).

2. Застосовуються «еквівалентні річні грошові потоки».

3. Передбачається, що довгостроковий проект продається на той момент, коли закінчується короткостроковий, і для обчис­лення NPV приймається його кінцева вартість.

Розглянемо це на конкретних прикладах.

Приклад І. Нехай фірмі необхідно порівняти два різні за тер­мінами дії проекти і вибрати серед них найефективніший за норми дисконту 16 %.

Проект А: інвестувати 60 000 грн. зараз з отриманням щорі­чного грошового потоку розміром 30 000 грн. протягом 6 років.

Проект Б: інвестувати 40 000 грн. зараз з отриманням щоріч­ного грошового потоку розміром 38 000 грн. упродовж 3 років.

Обчислимо NPV цих проектів:

При виборі проектів за показником NPV доцільно взяти проект А.

Проте зведемо ці проекти до порівнянного вигляду за згада­ними способами.

1. Якщо передбачати самовідновлення проекту Б, то маємо

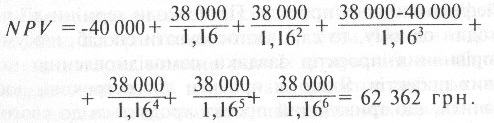
У цьому випадку показник NPV проекту Б перевищує зна­чення показника NPV проекту А, а тому доцільніше обрати про­ект Б.

2. Використовуючи еквівалентні річні грошові потоки, ви­ значимо суму ренти, яка протягом терміну дії кожного з проектів давала б однакові значення NPV, тобто так само, як і проек­ти, що розглядаються.

Для проекту А еквівалентний річний грошовий потік дорів­нюватиме

Оскільки проект з більшою сумою ренти даватиме й біль­ший прибуток, то в цьому випадку слід прийняти проект Б, бо він забезпечує більший еквівалентний річний грошовий потік, ніж проект А.

3. Використовуючи третій спосіб зведення проектів до порів­нянного вигляду, оцінимо остаточну (продажну) вартість проек­ту А після 3 років у 30 000 грн., тобто для поточного порівняння з проектом Б скоротимо термін, за який оцінюється проект А. Тоді NPV для проекту А буде дорівнювати

Отже і в цьому випадку доцільніше вибрати проект Б, оскіль­ки значення його показника NPV більше, ніж значення аналогіч­ного показника проекту А.

Виходячи з отриманих результатів, робимо висновок, що за­стосування способу еквівалентних річних грошових потоків є до­сить простим і водночас дає можливість зробити правильний ви­бір найефективнішого проекту. Проте коли терміни дії проектів кратні один одному, то слід застосовувати спосіб, що уможлив­лює порівняння проектів завдяки самовідновленню коротко­строкових проектів. Якщо ж проекти довгострокові, достатньо передбачити, що триваліший проект продається до свого завер­шення. Найголовніше — це не приймати рішення лише покладаючись на просте порівняння показників NPV проектів, розрахо­ваних на різні терміни дії.

Розглянуті методи оцінки і вибору інвестиційних проектів передбачали, що фірма (підприємство) володіє достатніми кош­тами, щоб інвестувати у будь-який проект. Але за умов перехід­ного періоду суб'єкти господарювання, як правило, знаходяться під впливом зовнішніх обмежень (жорстке нормування) щодо можливих джерел фінансового забезпечення інвестицій. За та­ких обставин вибір слід робити серед проектів, що мають пози­тивне значення NPV в умовах нормування інвестицій. Правиль­ний вибір у такому випадку можна зробити за допомогою інде­ксу доходності (рентабельності) R. Показник NPV виражає вартість інвестицій, а R — цю вартість з позицій питомої ваги необхідних первісних витрат. Таким чином, за дефіциту фондів обирається проект з більшим значенням R, оскільки прибуток від кожної вкладеної гривні буде більшим ніж для проекту з ни­жчим значенням R.

Розглянемо це на прикладі. Нехай компанія має капітал для інвестування розміром 100 000 грн. Проекти для аналізу пред­ставлені у табл. 3.6.

Ранжуючи проекти за критерієм зменшення значення показ­ника R, проекти С, А, Е приймаємо, а лишки інвестицій вкла­даємо у проект Б. Загальний розмір NPV становить: [40 000 + + 80 000 + 32 000 + (45 000/3)] = 167 000 грн. за умови можливості розподілу проектів на декілька (випадок з проектом Б). Проте на практиці це не завжди так і не всі доступні фонди можуть бути ви­трачені, якщо відібрані лише «цілі» проекти. Маючи за умову не­подільність проектів, можливі різні їх групування, які відповідати­муть бюджету витрат. У цій ситуації інвестор вибирає портфель проектів, залучаючи до нього ті, що дають максимальний розмір NPV (табл. 3.7).

Отже, у випадках, коли неможливо проект Б прийняти част­ково, найкращою комбінацією проектів буде А,Б,С. За нею за­гальний розмір NPV становить 165 тис. грн., що менше від 167 тис. грн. у випадку подільного проекту Б.

Таким чином, в умовах нормування капіталу вибір проектів з найбільшим значенням К забезпечує підприємству максималь­ний розмір показника NPV, а метод «портфеля» — відбір проек­тів, якщо вони неподільні.

При обранні проектів в умовах обмеження інвестицій най­більш прийнятним, хоч і більш складним, є метод лінійного про­грамування. За його допомогою можна віднайти оптимальне рі­шення, коли за критерій оптимальності береться максимізація значення NPV при дотриманні певних умов (у нашому випадку обмеження на капітал). Розглянемо застосування методу на кон­кретному прикладі.

Нехай у компанії є три інвестиційні проекти з позитивними

значеннями NРV (табл. 3.8).

Виходячи з обмежень на капітал, компанія не може прийня­ти псі три проекти. Протягом першого і другого років можна ін­вестувати лише 200 тис. грн., при цьому невикористані кошти не відноситимуться на наступний рік. Необхідні для здійснення інвестиційних процесів витрати наведені у табл. 3.9.

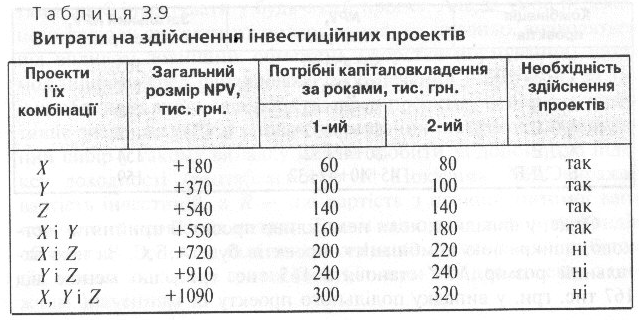
Враховуючи обмеження на капіталовкладення, віднайдемо максимальний розмір показника NPV проектів та їх комбіна­цій. Якщо розглядати лише перший рік, то доцільно обрати комбінацію X і Z, оскільки потрібні для них капіталовкладен­ня складають 200 тис, грн., а загальний розмір NPV — 720 тис. грн. Але якщо взяти до уваги наступний рік, то така комбіна­ція не задовольняє нашим умовам, адже капіталовкладення на їх реалізацію перевищують припустиму суму на 20 тис. грн. Тому найкращим варіантом, як для першого, так і для друго­го року, має бути комбінація проектів X і Y, бо загальний роз­мір показника NPV становить 550 тис. грн., а капіталовкла­дення не перевищують ліміти.

Розглянемо на прикладі розв'язок цієї задачі за методом лі­нійного програмування.

За мету береться максимізація загального розміру показника

NPV.

Розв'язання задачі здійснюється за допомогою стандарт­ної комп'ютерної програми МsЕхсеІ. Результати наведені у табл. 3.10.

Виходячи з отриманих результатів, оптимальне рішення за­безпечується при виборі комбінації X і У, що також узгоджу­ється з результатом за попереднім розрахунком. Переваги за­стосування методу лінійного програмування більш значимі, коли аналізується велика кількість інвестиційних проектів з багатьма обмеженнями. Застосування методу ітерацій є досить трудомістким.

Метод лінійного програмування — це один з найбільш ефе­ктивних засобів, за допомогою якого в умовах обмежених ресур­сів і низки інших вимог приймається оптимальне інвестиційне рішення.

Поряд з оптимізацією вибору інвестиційних проектів у пра­ктичній діяльності підприємців досить часто виникає проблема, пов'язана з розглядом цілого ряду привабливих інвестиційних проектів. Та внаслідок обмеженості ресурсів вони (або їх части­ни) не можуть бути реалізовані у плановому році одночасно, а тому цей процес переноситься на наступний рік. Розв'язок по­дібних задач зводиться до оптимального розподілу проектів за часом у такій послідовності.

По кожному проекту обчислюється індекс можливих втрат, що характеризує відносну втрату NPV у випадку, якщо проект виконуватиметься наступного року. Індекс втрат обчислюється за формулою

де NPV1 — чиста зведена вартість проекту, що розглядаєть­ся наприкінці першого року;

NPV0 — дисконтована величина NPV1, за процентною став­кою d, тобто

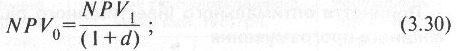
IС— розмір відкладених на рік інвестицій.

Реалізація проектів, що мають найменшу величину індексу можливих втрат, переноситься на наступний рік.

Розглянемо простий приклад складання оптимального плану розміщення інвестицій на два роки за умови, що заплановані на рік інвестиції не можуть перевищити 75 млн грн., а процентна ставка фінансування становить 10 %. Розглядається чотири альтернативні проекти (А, Б, В, Г) з такими потоками платежів (млн. грн.):

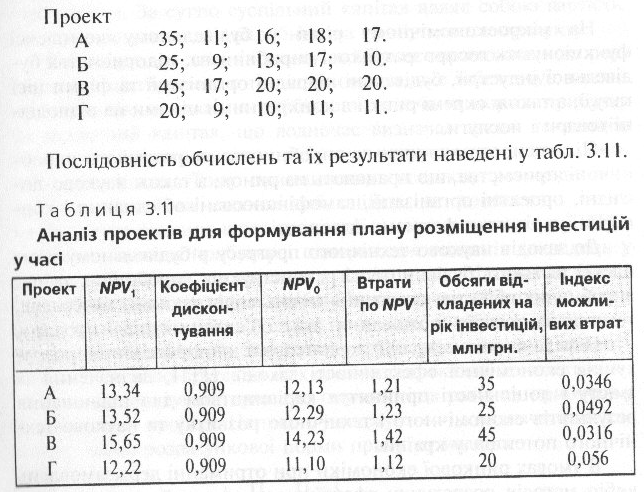
Найменші втрати забезпечуватимуться при перенесенні на наступний рік проекту В (I = 0,0316) і проекту А (I = 0,0346). Тому у поточному році для реалізації можуть бути прийняті про­екти Б і Г у повному обсязі, а оскільки загальна сума їх інвес­тицій не перевищує 75 млн. грн. (вона складає 45 млн. грн.), то в цьому ж році може бути реалізована і частина проекту А. Іншу частину проекту А і проект В повністю доцільно реалізувати на­ступного року.

Таким чином, при виборі найбільш ефективного інвестицій­ного проекту серед багатьох з однаковими характеристиками надходжень грошових потоків але з різними термінами дії слід передусім звести їх до порівнянного вигляду, а потім за допомо­гою запропонованих методів проводити оцінку. Для умов з об­меженими ресурсами, характерних для перехідного періоду еко­номіки, найбільш придатним для вибору найефективнішого ва­ріанту реалізації інвестиційних проектів з позитивними значеннями NPV є метод лінійного програмування з урахуван­ням індексу можливих втрат.