Закон Стефана – Больцмана.

Он имее отношение к излучающей способности тела. В законе показано, что излучающая способность тела пропорциональна 4 степениот температуры поверхности тела. Кроме того установлено, что излучать могут только тела, близкие к черным( что хорошо поглощает, то хорошо и излучает ). Прозрачные тела и белые излучают плохо, абсолютно прозрачные и абсолютно белые не излучают вообще.

– энергия излучения абсолютно черного тела

– коэффициент излучательной способности абсолютно черного тела

Для серых тел:

– коэффициент излучательной способности серого тела

𝜉 – степень черноты поверхности

(для полированного аллюминия)

(для углеродистой стали)

(для резины или сажи)

(для эталона черноты)

Закон Киргофа.

Закон устанавливает зависимость между поглощающей и излучающей способностью тел. В соответствии с законом отношение излучающей способности к поглощающей при постоянной тмпературе. Если величина постоянная и равная излучающей способности абсолютно черного тела, то:

Закон Ламберта.

Закон устанавливает связь между энергией излучения и направлением по отношению к излучающей поверхности.

Е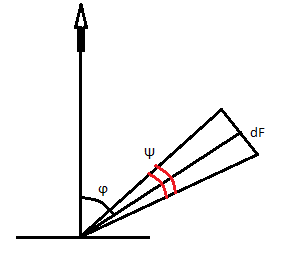 сли поверхность излучает полную энергию Е, то на приемник площадью dF попадает часть излучения dQ

5.11.10.

В направлении перпендикулярном к поверхности излучения энергия будет в раз меньше полной энергии. В случае взаимного излучения тел одно тело излучает, а другое поглощает энергию. В этом случае передача энергии зависит от излучательной или испукательной способности того тела, у которого она меньше.Рассмотрим трубопровод, экранированный теплоизоляцией.

В этом случае поток энергии будет направлен от внешнего экрана к внутренней трубе.

– коэффициент закрытия экрана( – полностью окружен)

– излучающая способность абсолютно черного тела

; , – степени черноты трубопровода и экрана соответственно.

При расчете теплообменных аппаратов, которые находятся в открытой газовой среде и имеют температуру выше этой среды, то от этих аппаратов исходит и излучение и теплопередача конвекцией. Использование обоих факторов возможно при использовании эмпирического уравнения, например для теплового тела в воздухе:

; – коэффициент теплопередачи.

Теплопередча за счет конвекции и теплопроводности.

Рассмотрим поток жидкости, текущей по трубе, при этом температура трубы отлична от температуры жидкости. В этом случае будет проходить теплопередача, причем в пристеночной области, поскольку жидкость неподвижна, теплопередача будет за счет теплопроводности жидкости. По мере удаления от стенки в жидкости появляются скоростные эфекты, которые могут приводить к появлению конвективных потоков. В этом случае имеется зависимость теплопередачи внутри жидкости от скорости ее движения. Возможно так же искуственное перемешивание жидкости, которое так же приводит к конвективной теплопередаче. Конвективный поток приводит к выравниванию температуры в толще жидкости, но она остается распределенной от ядра к стенке.

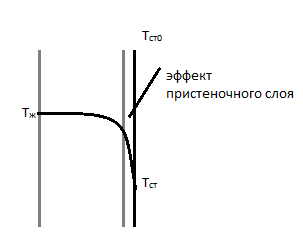В общем случае поток описывается уравнением

Уравнение Ньютона

В заложены все ньюансы перехода тепла в толще жидкости и к стенке. Очевидно, что будет зависеть от теплопроводности жидкости, вязкости, скорости и др. Для вычисления необходимо уравнение, которое описывало бы все возможные пути распространения тепла в жидкости. Такое уравнение предложени Фурьеи Кхиргоффом.

Уравнение имеет 2 ограничения:

1. Поток неразрывен

2. Турбулезация установилась

Выделим в потоке неподвижный параллелепипед, с гранями . Пусть – это колическтво тепла, которое входит в параллелепипед за счет конвекции по направлению оси .

; – массовая теплоемкость

Пусть на длинне dx за счет конвекции идет прирост тепла на . Найдем прирость дифференцированием:

Если прирост тепла существует по всем направлениям, то общий прирост будет суммой:

=0

Если поток неразрывен, то , а

Наряду с этим тепло приростает так же и за счет теплопроводности, как было показано выше:

Прирост тепла в элементарном обьеме приводит к увеличению внутренней энергии:

Если теплопередача прошла за счет конвекции и за счет диффузии, то:

Уравнение Фурье – Кирхгофа

– коэффициент теплопроводности.

Уравнение учитывает распространение тепла за счет конвекции и теплопроводности. Для установленного теплового потока . Видно, что если скорость движения жидкости равна нулю, то уравнение уравнение превращается в уравнение теплопроводности.

Уравнение теплового подобия.

При теплопередаче осуществляется 2 процесса, один изних связан с общим тепловым потоком от ядра потока к стенке(уравнение Ньютона), а другой связан с теплопроводностью жидкости в пристеночной области и описывается уравнением Фурье:

После подобного преобразования получим :

Критерий Нусильда,он характеризует отношение суммарной скорости потока к скорости потока за счет теплопроводности.

Если известен Nu, то возможно вычислить . Для определения численного значения Nu используют критериалное уравнение, в которое входят определяющие критерии теплового подобия, полученные при подобном преобразовании уравнения Фурье – Кирхгоффа

1 2 3

1. Характеризует нестационарность процесса.

2. Конвективную составляющую процесса.

3. Теплопередачи за счет теплопроводности.

Тепловой критерий Фурье,отражающий нестационарность процесса.

Критерий Пекле, отражающий отношение теплопередачи за счет конвективности к теплопередаче за счет теплопроводности.

На базе критерия Pe выведим составной критерий :

Критерий Пракотля(?) – характеризует физическое свойство теплоносителя.

для газов и для сотен жидкостей. входит в состав критериальных уравнений , связывающих определяемый критерий Nu С определяющими критериями Re и Pr.

Gr Pr	C*	n
	1.18	0.125
500 Gr Pr 2 107	0.54	0.25
2 107	0.135	0.33

и n –const, которые зависят от (Gr Pr)

Если теплопередача сопровождается изменением агрегатного состояния, то конденсат может образовываться либо в виже тумана, либо в виде пленки на поверхности конденсации. Образование пленки наиболее желательно для эффективной конденсации. Для этого случая :

Критерий конденсации

Скрытая энтальпия конденсации

Теплоемкость Разность температур между поверхностью и паром

(обычно ∆T берут 3 )