Зависимость перепада давления от скорости газа.

Зависимость перепада давления от скорости газа. Скорость выхода на кипящий слой приводит к стабилизации перепадов давления и называется первой критической скоростью. За второй криттической скоростью происходит унос вспученного материала.

П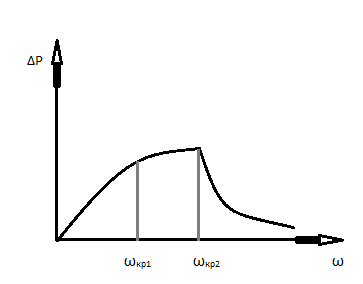 остоянство перехода давления является основой для теории расчета первой и второй критичеких скоростей. Перепад давления в режиме фильтрации описан в уравнеии Эриана:

При переходе в кипящий слой частицы подвисают, т.е. сила тяжести уравновешивается силой давления, действующей на частицу. Сила давления на частицу связаня с переходом : ; S - площадь сечения частицы.

Перейдем от V и S к V,ρ,S. Так как число частиц постоянно, то частицы пропорциональны объему реактора, а площадь сечения частицы пропорциональна площади сечения реактора.

отсюда найдем :

С другой стороны ;

; или

Подставляем:

Существует такая возможность расчета скорости кипящего слоя с помощью имперического критериального уравнения.

Процессы разделения неоднородных систем.

Неоднородные системы состоят из нескольких неоднородных фаз. Фаза характеризуется однородным состоянием иагрегатным состоянием. В неоднордных системах различают дисперсную фазу и дисперсную среду. Дисперсная фаза- это частицы, а дисперсная среда(сплошная)- фаза, в которой частицы распределены. Диспесрсной фазой может быть так же жидкость или твордое тело, газ. Сплошной средой может быть газ или жидкость.

Дым -это твердые частицы,конденсация конденсация которых происходит в газе.

Туман - это жидкие частицы, конденсация которых происходит в газе.

Суспензия – это твердые частицы в жидкости.

Эммульсия – жидкие или газообразные частицы в жидкости.

В дисперсной фазе бывают частицы различных размеров:

1. Грубые дисперсии ( р-р 100 мкм )

2. Средние дисперсии ( 1-100 мкм )

3. Тонкие дисперсии (0.5-1 мкм )

4. Муть ( 0.1-0.5 мкм )

5. Коллойдные частицы ( 0.1 мкм )

Муть и коллойдные частицы практически не оседают, но в них возможна коагуляция ( укрупнение за счет слипания ) коалисценция ( оседания крупных частиц ).

Уравнение материального балланса при разделении неоднородных систем.

Уравнение материального балланса можно составить по 2 направлениям:

1. Материальный баланс по потокам

2. Материальный баланс по веществу

Схема отстойника:

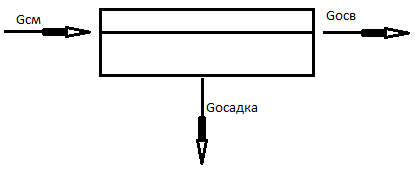
В отстойник втекает жидкость с массовы расходом . В отстойнике жидкость осветляется и вытекает. Осветленная с массовым расходом , а так же в виде концентрированного осадка с массовым расходом . Балланс по потокам .

Пусть в мутной жидкости содержится дисперсная фаза с массовой долей . В осветленной жидкости будет массовая доля , а в осадке- . Можно составить балланс по веществу:

– баланс сотавляется поприходу и уходу вещества.

; ; ;

Разрешим уравнение относительно :

Уравнение материального баланса работы отстйника.

Методы разделения жидких неоднородных систем.

Существует 3 метода разделения:

1. Отстаивание – осаждение частиц под действием силы тяжести. Применяется для очистки грубых систем и как предварительная стадия очистки полудисперсных систем.

2. Центрифугирование – разделение под действием центробежной силы. Применяется для любых систем.

3. Фильтрование – процесс разделения с помощью пористой перегородки, проницание жидкости через перегородку обеспечивается разностью давлений до и после перегородки. Применяется для отделений сред и тонких дисперсий. Ультрамикрофильтрация применяется идля коллойдных систем.

В процессе отстаиванияпроисходит постепенная концетрация частиц по направлению сверху вниз. Верхняя зона с минимальной концетрацией частиц называется осветленной. Ниже расположена зона, в которой частицы оседают, не сталкиваясь друг с другом. Это зона свободного осаждения. Ниже частицы оседают стесненно, так как концетрация их возрастает и они начинают сталкиваться друг с другом. При этом крупные частицы догоняют мелкие и ударяют их. В результате скорость осаждения мелких частиц возрастает, а крубных убывает, в среднем скорости выраниваются.

Кроме того, оседающие частицы вызывают поток жидкости снизу вверх, так как вытесняют ее. Встречный поток жидкости затрудняет осаждение, поэтому в зоне стесненного осаждения концетрирование осадка происходит медленно.

Расчет скорости отстаивания.

Эта методика распространена на зону свободного осаждения и для сферических частиц. Допускается, что на частицу действует силя тяжести, а впротивоположную сторону сила Архимеда. Если , то возникает ускоренное движение, которое вызывает появление силы сопротивления жидкости, которая зависит от скорости.

При некоторой скорости все силы уравновешиваются и в результате крость частицы становится равномерной.

;

R – сила сопротивления, Ar – сила Архимеда;

;

;

– масса вытесненного растворителя;

;

;

𝜉 - коэффициент сопротивления жидкости ; ;

15.10.10.

Другой вариант расчета скорости осаждения по методике Лященко.

; т.к.

, то

Видно, что предположенное уравнение Лященко позволяет вычислить без использования параметров трудно определить эксперементально. Затем, используя вычисленный , расчитываем

Кроме того, скорость осаждения можно оценить по критериальному уравнению:

• – для ламинарного потока.

• – для любого режима осаждения.

Расчет площади отстаивания отстойников.

Поскольку высота осветленного слоя зависит от физико – химических свойствжидкости, твердые частицы и размера дисперсии, то на производительность отстойника можно повлиять лишь через площадь отстаивания. Объемный расход осветленной жидкости:

; – время осаждения, - высота освещенного слоя, – площадь остаивания.

;

Перейдем от объемного расхода к массовому:

В уравнении балланса поделим левую и правую часть на :

При использовании этого уравнения залают массовый расходи использованной смеси . Содержание в использованной смеси дисперсной фазы , содержание дисперсной фазы в осадке , а так же содержание дисперсной фазы в осветленной жидкости . Задав эти параметры можно расчитать площадь отстаивания, после предварительного расчета скорости отстаивания.

Если , то F будет убывать

Реальную площадь отстаивания на 25% больше расчитанной из-за влияния несферичности частиц, что приводит к уменьшению площади осажденя.

Центрифугирование.

Разделение идет под действием центробежной силы. Если центрифугирование совмещают с фильтрацией, то это тоже относится к центрифугироавнию. Из-за общности подхода к отстаиванию под действием силы земного притяжения и под действием центробежной силы основной характеристикой эффективности центрифугирования является отношение центробежного ускоренного с ценробежному свободному падению.

; ; ;

n-количество оборотов центрифуги в секунду,

r-радиус центрифуги,ω-окружность скорости(?)

– коэффициент эффективности центрифуги

Видно, что на обороты центрифуги влияют больше, чем радиус, поэтому на центрифугах указывают количество оборотов в минуту. В обычных центрифугах около 3.5 тысяч при 5-10 тысячах оборотов, а в сверхцентрифугах более 40 тысяц обротов в минуту, при этом 15 тысяч.

Для сравнения скорости отставивания в обычном отстойнике и центрифуге применяют индекс производительности центрифуги. Он показывает, во сколько раз скорость очистки в центрифуге больше скорости очистки в отстойнике.

Численно индекс производительности равен .

Фильтрование.

Процесс освобождения дисперсной фазы при прохождении дисперсной среды через простую перегородку под действием перепада давления. Для описания процесса фильтрации применяется медот свзывания с движущей силой сопротивления фильтра и осадка.

-основное уравнеия фильтрования.

W – скорость фильтрации, V – объем фильтруемой смеси, S – площадь фильтра, ∆P – перепад давления, μ – вязкость, – сопротивление осадка и перегородки.

Существуют 3 варианта проведения процесса фильтрации:

• Фильтрование при постоянном перепаде давления

• Фильтрование при постоянной скорости фильтрации за счет переменного давления

• Фильтрование при постоянном перепаде и постоянном давлении(для промывки фильтра)

Фильрование при постоянном перепаде давления.

Скорость фильтрации перемена, так как толщина осадка непрерывно растет и сопротивление возрастает.

– удельное сопротивление осадка, приведенное к единице его толщины, – толщина осадка

Пусть – это отношение объема осадка к объему фильтрата, тогда

– объемная доля осадка; ;

Для удобнее вместо полного объема фильтрата применять удельный объем

основное уравнение для расчета удельного объема фильтрата.

Фильрование при постоянной скорости.

Запишем аналитическое уравнение фильтрования с учетом постоянной скорости

– удельная скорость фильтрации

Урвнение позволяет удельную скорость фильтрации при перепаде давления ∆P

Фильтрация при постоянном перепаде давления и скорости.

Такой процесс реализуется при промывке фильтра. Ее ведут путем пропускания небольшого количества фильтрата через фильтр в обратную сторону. При этом осадок с фильтрующей стороны смывается.

=0

– объем жидкости, используемый для промывки

Расчет параметров фильтрации.

Все приведенные уравнения включают такие параметры, как . Для их определения проводят эксперемент на лабораторной установке. В результате эксперемента определяют зависимость удельного объема фильтрата от t. При постоянном перепаде дывления уравнение имеет вид:

Строят график в координатах XY и эта зависимость линейна. Причем, отрезок отсекающий от оси ординат, позволяет вычислить и тангенс угла наклона - .

Оптимизация процесса фильтрования с точки зрения экономики.

В производственных процессах фильтрование невозможно сделать непрерывным. Это связано с тем, что слой осадка непрерывно растет, скорость фильтрования падает и возникает необходимость переодически останавливать производственный процесс и выполнять не произвольную работу, связанную с очисткой фильра. С другой стороны, чем чем чаще чистим фильтр, тем большей скорости фильтрования достигаем в производственном цикле. Поэтому существует оптимальная периодичность очистки фильтра, позволяющая достич максимальной скорости фильтрации.

Обозначим полное время работы фильтра как . Это время включает в себя период основной работы фильтра и вспомогательной, связанной с очисткой фильтра . Пусть фильтрация идет при постоянном ∆Р, тогда:

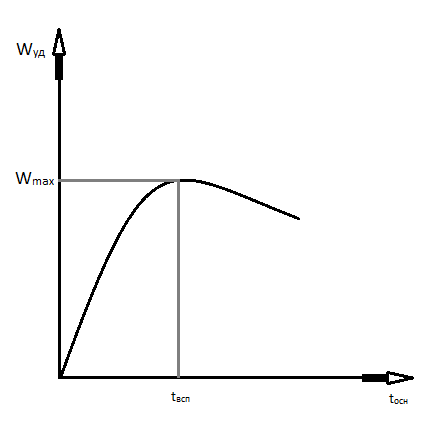
Пусть сопротивление пренебрежительно мало по сравнению с осадком, тогда: