Теорема подобия. Гидродинамическое подобие.

Уравнение Навье-Стокса-это дифференциальное уравнение, поэтому его решение сводится к нахождению функции,дифференциал которой представлен в данном уравнении. Суть гипотезы о подобии в том, что это уравнение в интегральной форме является одинаковым во всех подобных процессах и не зависит от способа релизации этого процесса.

Например, на отрезке трубопровода течет вода по одинаковым трубам, с одинаковой скоростью, с одинаковым заполнением трубы, в одном случае под действием насоса, а вдругом под действием гидростатического напора. Считают,что все характеристики движения жидкости одинаковы,если да,то гипотеза о подобии принята.

Теорема о подобии(доказана Кирпичевым).

Подобны те явления,которые описываются одной и той же системой дифференциальных уравнений, и у которых условия однозначности решения подобны. Применение теоремы о подобии позволяет не искать саму функцию, дифференциал которой представлен в уравнении, поскольку эта функция одинакова из-за условия однозначности интегрирования.Это дает право применить подобные преобразования к дифференциальным уравнениям.

Исключим из рассмотрения направления “x” и ”z”. Останется только “y”:

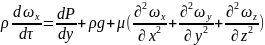
1 2 3 4

1-сила инерции 3-сила тяжести

2-сила давления 4-сила внутреннего трения

Запишем полный дифференциал ускорения 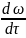через частные производные по всем направлениям

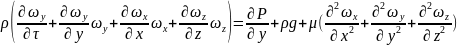
Это уравнение можно подвергнуть подробному преобразованию, которое завключается в убирании знаков математических операций и переходе от бесконечно малых приращений к конечным величинам.

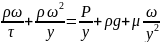
1 2 3 4 5

1-отражает силу инерции в нестационарных условиях

2-сила инерции для стационарного потока жидкости

3-это сила гидростатического давления

4-силя тяжести

5-сила внутреннего трения

Поскольку функции не известны, но принята гипотеза о подобии, то для практического использования возможно применение соотношения различных сил. Например соотношение:

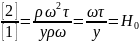. Соотношение сил называется критерием подобия. -Критерий гомохромности. Его Величина позволяет оценить соотношение стационарно и нестационарной составляющей потока.

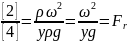- Критерий Фрудо

Позволяет оценить, под действием каких сил движется жидкость.

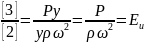- Критерий Эйлера

Показывает соотношение сил гидростатического давления,кроме инерции. Поэтому часто вместо 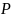используют 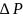, который показывает разность гидростатического давления нак концах трубопровода.

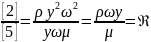- Критерий Ренольдса.

Показывает отношение силы инерции с силам трения. Сыли инерции характеризуют силы невязкой жидкости. Все критерии величины безразмерные по определению, т.к. это соотношение сил. Это просто число, величина которого характеризует какой-либо параметр в течении жидкости. Например, если 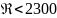, то поток ламинарный. Если 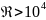, то характер течения жидкости турбулентный, а в промежутке переходный.

Кроме того существует производный критерий, который является комбинацией основных.

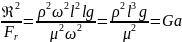– Критерий Галилея

Критерий удобен для описания движения жидкости в условии свободной конвекции. Удобство заключается в отсутствии скорости, т.к. она трудно определяется. Производная критерия 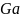по отношению к ρ дает критерий:

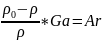- Критерий Архимеда

Среди основных критериев существуют определенные и определяющие.

Определяющие критерии включают в себя параметр,входящий в граничные условия находимого дифференциального уравнения, т.е. связаны с условиями однозначиности и не содержат произвольных параметров.

Определяемые критерии включают в себя произвольно измененные параметры.Среди известных-определяемый критерий Эйлера, он включает величину .