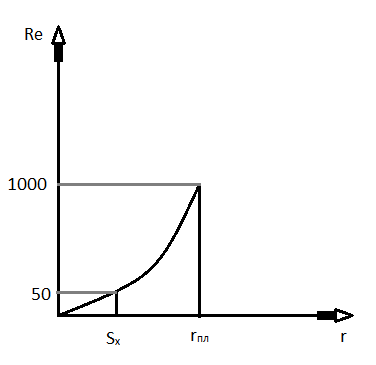
- •Классификация основных процессов химических технологий.
- •Гидродинамика.
- •Основное уравнение гидродинамики - уравнение неразрывности потока.
- •Теорема подобия. Гидродинамическое подобие.
- •Теорема о подобии(доказана Кирпичевым).
- •Расчет гидравлического сопротивления трубопровода.
- •- Критерий Грасгоффа
- •Перемещение жидкости.
- •Определение мощности насоса, работающего на всасывании и нагнетании.
- •Многоступенчатаое сжатие.
- •Гидродинамика псевдоразжиженного слоя(кипящего).
- •Зависимость перепада давления от скорости газа.
- •Процессы разделения неоднородных систем.
- •– Это зависимость экстримальная.
- •Теплопередача.
- •– Тепловой поток, – коэффициент теплопередачи, – площадь теплообменника, – разность температур
- •Закон Стефана – Больцмана.
- •Теплопередча за счет конвекции и теплопроводности.
- •Расчет коэффициента теплообмена.
- •Выпаривание.
- •Расчет температуры кипения раствора.
- •Многокорпусные выпарные установки.
- •Основы массопередачи.
- •Уравнение рабочей линии.
- •Материальный баланс :
- •Перенос компонентов жидкости и паре.
- •Теория Данхверста
- •Уравнение массообмена. Закон аддитивности фазовых сопротивлений.
- •Закон аддитивности фазового сопротивления.
Уравнение рабочей линии.
Из определения
коэффициента разделения следует, что
в случае
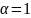 разделить эту смесь невозможно. Для
разделения таких смесей используют
процессы, в которых
разделить эту смесь невозможно. Для
разделения таких смесей используют
процессы, в которых
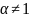 .
Уравнение рабочей линии применяют для
компонентов рабочей смеси с отличным
от 1 коэффициентом разделения. Уравнение
рабочей линии выводят для аппарата,
работающего в стационарном режиме, при
этом используют уравнение материального
баланса. Рассмотрим тарельчатую колонну.
Пусть расход жидкости в ней L,
расход пара G
.
Уравнение рабочей линии применяют для
компонентов рабочей смеси с отличным
от 1 коэффициентом разделения. Уравнение
рабочей линии выводят для аппарата,
работающего в стационарном режиме, при
этом используют уравнение материального
баланса. Рассмотрим тарельчатую колонну.
Пусть расход жидкости в ней L,
расход пара G
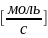 .
.
Пусть на
самую нижнюю тарелку с расходом
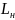 втекает жидкость состава
втекает жидкость состава
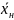 ,
тогда количество втекающего компонента
равно
,
тогда количество втекающего компонента
равно
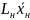 .
Пусть из тарелки вытекает жидкость с
расходом
.
Пусть из тарелки вытекает жидкость с
расходом
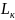 и состава втекает жидкость
и состава втекает жидкость
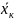 , тогда количество втекающего компонента
равно
, тогда количество втекающего компонента
равно
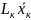 . Пусть на тарелку поступает пар с
расходом
и концентрацией
. Пусть на тарелку поступает пар с
расходом
и концентрацией
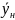 ,
тогда на тарелку поступает
,
тогда на тарелку поступает
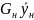 пара. А уходит с тарелки
пара. А уходит с тарелки
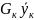
Материальный баланс :
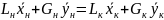
Это уравнение
можно распространить на всю колонну,
если по колонне не производится отбора
с тарелок. Рассмотрим баланс для самой
нижней тарелки и любой произвольной
тарелки, на которую приходит жидкость
с расходом
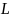 и состава
.
С нижней тарелки с расходом
стекает жидкость с концентрацией
,
на нижнюю тарелку поступает пар с
расходом
и
и состава
.
С нижней тарелки с расходом
стекает жидкость с концентрацией
,
на нижнюю тарелку поступает пар с
расходом
и
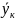 ,
с произвольной тарелки уходит пар с
расходом G и концентрацией
компонента y.
,
с произвольной тарелки уходит пар с
расходом G и концентрацией
компонента y.

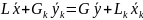 Все концентрации выражены в мольных
долях, а G и L
мольные расходы :
Все концентрации выражены в мольных
долях, а G и L
мольные расходы :
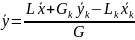
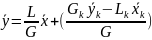
Если
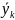 и
и
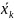 и соответствуют составу исходной
загрузки, т.е. являются постоянными
параметрами. Следовательно, уравнение
зависимости
и соответствуют составу исходной
загрузки, т.е. являются постоянными
параметрами. Следовательно, уравнение
зависимости
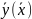 – это прямая вида
– это прямая вида
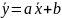 .
Тогда на графике можно отразить составить
жидкости и пара в любом произвольном
сечении колонны, где y –
состав пара, а x - состав
жидкости.
.
Тогда на графике можно отразить составить
жидкости и пара в любом произвольном
сечении колонны, где y –
состав пара, а x - состав
жидкости.
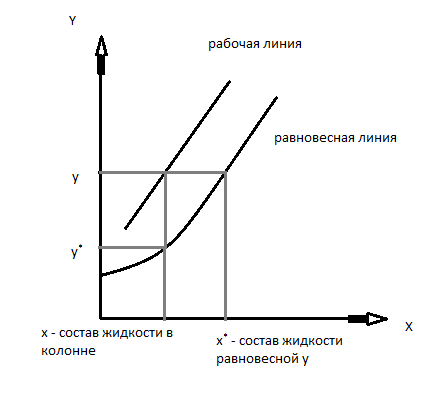
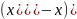 – движущая сила процесса массопередачи
в жидкости. Но в произвольном сечении
колонны мы имеем состав жидкости х, в
паре в этом же сечении состав пара у,
равновесным должен быть
– движущая сила процесса массопередачи
в жидкости. Но в произвольном сечении
колонны мы имеем состав жидкости х, в
паре в этом же сечении состав пара у,
равновесным должен быть
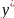 .
.
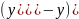 – основная движущая сила процесса
массопередачи в паре.
– основная движущая сила процесса
массопередачи в паре.
Выбор основной движущей силы связан с тем, какая из фаз больше сопротивляется массопередаче. Движущую силу выбирают для той фазы, для которой выше сопротивление массопередачи.
Если колонна работает в стационарном и бесотборном режиме, то количество компонентов, их концентрации и мольные расходы постоянны, следовательно :
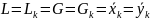
Подставив в
уравнение рабочей линии получим, что
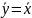 .
В стационарном и безотборном режиме в
любом произвольном сечении колонны
состав жидкости и пара одинаков.
.
В стационарном и безотборном режиме в
любом произвольном сечении колонны
состав жидкости и пара одинаков.
Перенос компонентов жидкости и паре.
Перенос вещества внутри жидкости или газа происходит за счет конвекции, а вблизи границы раздела фаз за счет диффузии. Объем перенесенного вещества по диффузионному механизму может быть расчитан по уравнению Фика :
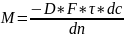
D
– коэффициент диффузии, F
– площадь,
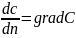 – распределение концентрации в
направлении n.
– распределение концентрации в
направлении n.
D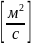 – отражает количество вещества,
проходящего в единицу времени через
еденицу площади при перепаде концентрации
1. Коэффициент диффузии функция от физико
– химических свойств как растворителе,
так и растворенного вещества. В газах
коэффициент диффузии от 1 до 0.1 , в
жидкостях в 10-100000 раз меньше.
– отражает количество вещества,
проходящего в единицу времени через
еденицу площади при перепаде концентрации
1. Коэффициент диффузии функция от физико
– химических свойств как растворителе,
так и растворенного вещества. В газах
коэффициент диффузии от 1 до 0.1 , в
жидкостях в 10-100000 раз меньше.
Конвективный перенос массы связан с перемешиванием внутри потока, связан с его турбулезацией и поэтому зависит от гидродинамики движущейся среды. Объем вещества перенесенный за счет конвекции записывается как :
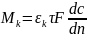
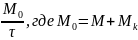
Тогда суммарная
скорость переноса вещества
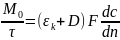
В жидкости
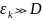 ,
а в газах
,
а в газах
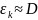
Дифференциальное уравнение конвективной массопередачи.
Вывод уравнения
аналогичен выводу уравнения для
теплопередачи. Выделим в пространстве
элементарный параллелепипед с гранями
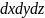 .
Рассмотрим количество входящего и
выходящего вещества, при этом предположим,
что прирост вещества происходит и за
счет конвекции и за счет диффузии. По
направлению
прирост вещества будет
.
Рассмотрим количество входящего и
выходящего вещества, при этом предположим,
что прирост вещества происходит и за
счет конвекции и за счет диффузии. По
направлению
прирост вещества будет
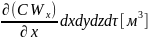 – прирост объема вещества. Дифференциал
произведения
– прирост объема вещества. Дифференциал
произведения
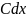 можно разбить на две составляющие :
диффузионную и конвективную.
можно разбить на две составляющие :
диффузионную и конвективную.
За счет
диффузии:
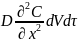 .
.
За счет
конвекции прирост будет:
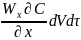
Тогда общий
прирост объема будет:
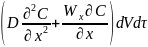
Если перенос вещества идет по всем трем направлениям, то :
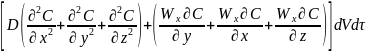
Прирост
объема вещества в элементарном
параллелепипеде приведет к изменению
концентрации в нем
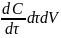 . После прироста объема и прироста
концентраций и сокращений однородных
величин получим :
. После прироста объема и прироста
концентраций и сокращений однородных
величин получим :
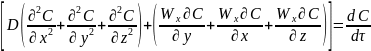
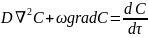
Если режим
стационарен, то
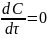 ,
а если отсутствует и конвективный
перенос, то
,
а если отсутствует и конвективный
перенос, то
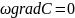 ,
следовательно :
,
следовательно :
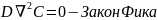
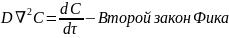
Подобные преобразования дифференциального уравнения.
Подобные преобразования дифференциального уравнения массопередачи :

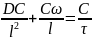
2 3 1
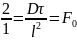
Критерий Фурьедля диффузионных процессов свзан с нестационарностю :
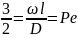
Диффузионный критерий Пекле. Отражает отношение между конвективной массопередачей (3) и диффузионной (2).
Для расчета скорости
массопередачи используют так же
диффузионный критерий Нусельда. Этот
критерий получен из уравнения
массопередачи. Это уравнение требует
модельных представлений о механизме
передачи массы из одной фазы в другую,
а так же о механизме переноса вещества
из глубины фазы к границе раздела. Пусть
в глубине фазы концентрация компонента
будет Y в паровой фазе и
X в жидкой, тогда объемная
скорость массопередачи будет
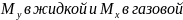 . Пусть на границе раздела фаз равновесие
устанавливается мгновенно, тогда на
самой границе появятся концентрации
. Пусть на границе раздела фаз равновесие
устанавливается мгновенно, тогда на
самой границе появятся концентрации
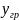 и
и
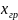 отличные от концентрации в толще
жидкости.
отличные от концентрации в толще
жидкости.
Т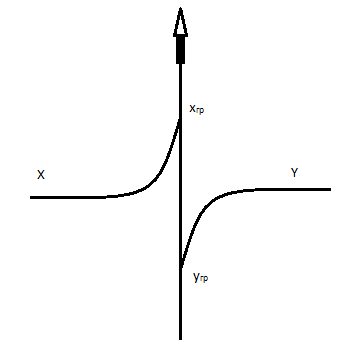 очно
такая же картина будет наблюдаться и в
случае использования относительных
мольных концентраций X
Y, тогда с учетом мгновенного
установления равновесия на границе
раздела фаз
очно
такая же картина будет наблюдаться и в
случае использования относительных
мольных концентраций X
Y, тогда с учетом мгновенного
установления равновесия на границе
раздела фаз
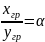 .
В этом случае основная движущая сила
массопередачи в жидкой фазе будет
.
В этом случае основная движущая сила
массопередачи в жидкой фазе будет
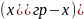 ,
а в паровой фазе
,
а в паровой фазе
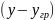 .
.
Область, в
которой происходят затруднения
массопередачи называется диффузионной
– это приграничная область, в которой
практически нет движения жидкости или
пара, поэтому перенос массы в ней идет
только за счет молекулярной диффузии.
Пусть толщина приграничной области
будет
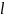 ,
тогда перенос вещества в этой области
будет :
,
тогда перенос вещества в этой области
будет :
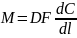
С другой стороны скорость массопередачи будет зависеть от движущей силы следующим образом
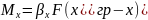
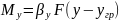
Тогда в общем виде скорость массопередачи будет :
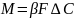
Сравнивая это уравнение с диффузионным получим :
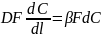
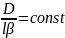
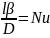
Получаем диффузионный критерий Нусельда.
Тогда для жидкости :
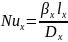
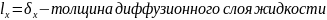
Скорость диффузионного слоя равна нулю, конвективного переноса внутри массы нет, а реализуется только молекулярная диффузия. В паровой фазе диффузионный слой не выражен, поэтому :
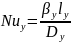
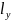 – эквивалентный диаметр парового
потока.
– эквивалентный диаметр парового
потока.
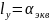
Критерий
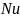 является определенным, поэтому его
расчитывают с помощью критериальных
уравнений :
является определенным, поэтому его
расчитывают с помощью критериальных
уравнений :
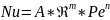
Где
 – экспериментальные данные, занесенный
в справочник.
– экспериментальные данные, занесенный
в справочник.
Целью расчета
являются
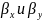 - эти коэффициенты являются характеристикой
скорости массопередачи. Полученные
уравнения вытекают из двупленочной
модели массопередач. Эту теорию развивали
Ландау и Лившиц под названием “Теория
пограничного диффузионного слоя”.
Слабым местом модели является толщина
диффузионного слоя. В связи с этим
Ладндау и Нишец дали рекомендации по
расчету этой толщины. Рекомендации
основаны на доказательстве того, что
коэффициент турбулезации потока
пропорционален квадрату расстояния
границы раздела фаз.
- эти коэффициенты являются характеристикой
скорости массопередачи. Полученные
уравнения вытекают из двупленочной
модели массопередач. Эту теорию развивали
Ландау и Лившиц под названием “Теория
пограничного диффузионного слоя”.
Слабым местом модели является толщина
диффузионного слоя. В связи с этим
Ладндау и Нишец дали рекомендации по
расчету этой толщины. Рекомендации
основаны на доказательстве того, что
коэффициент турбулезации потока
пропорционален квадрату расстояния
границы раздела фаз.