Классификация основных процессов химических технологий.

В химической технологии помимо процессов, связанных непосредственно с химической реакцией, протекают так же многочисленные физические, механические, физико - химические процессы: перемешивание жидкостей, газов, фильтрация, нагрев, охлаждение, испарение, конденсация, сушка, разделение смесей и прочее.

Все эти процессы общие для разнообразных определений химических технологий и связано с химическим производством. В связи с этим данные процессы называются базовыми.

Главный вопрос любого процесса химической технологии - это вопрос о скорости протекания реакции. Усилия ученых - технологов так или иначе направлены на организацию процессов или создание аппарата, реализующего максимально возможную скорость протекания процесса.

Достижение максимальной скорости возможно в результате изучения законов на потенциальном барьере данных процессов. Для удобства процессы классифицируют по тем законам, на которых они основаны:

1. Гидромеханика - Процессы, связанные с перемешиванием жидкостей и газовой среды, описание их статической составляющей, перемешиванием, разделением неоднородных сред и центрифугированием.

2. Тепловые, Теплопередача - скорость процесса определяется законами о способе передачи тепла: нагрев, охлаждение, испарение, конденсация.

Скорость теплопередачи зависит от теплопроводности, скорость передачи тепла излучением. Таким образом перемешивание внутри объёма жидкости или газа влияет на скорость теплопередачи (изучает гидромеханика).

3. Массообмен, массоперенос - процесс связанный с изменением концентрации во времени внутри одной или нескольких фаз в какой либо практической точке. Чаще всего процесс массопередачи связанный с деформацией, поэтому эти процессы еще называют диффузионными. К массообменным процессам относится абсорбция, адсорбция, ректификация, экстракция, кристаллизация, дистилляция, сушка. Скорость распространения реагента в жидкой или газовой фазе зависит не только от скорости диффузии, но и от скорости конвективного перемещения внутри объема жидкости или газа, поэтому 3-й процесс связан с 1-м. Кроме того, процесс массопереноса часто связан с тепловыми эффектами, таким образом 3-й вид включает в себя 2-й.

4. Стоит особняком и связан с механикой твердого тела. К этим процессам относятся: измельчение, резка, шлифовка, полировка, отсеивание, а так же литье.

Гидромеханические процессы.

Гидромеханика изучает действие сил в жидкостях. Включает в себя гидростатику (распределение сил в неподвижной жидкости) и гидродинамику (распределение сил в движущейся жидкости). Для решения уравнений гидромеханики часто используют приближенное описание жидкости.

1-е приближение называют идеальная жидкость (несжимаемая и невязкая жидкость)

2-е приближение называют реальная жидкость (несжимаемая, но вязкая)

3-е приближение называют упругая жидкость (невязкая, но несжимаемая).

Основные свойства жидкостей и газов.

• Плотность ρ=m/V

Плотность газов при не большом давлении хорошо описывается уравнением Менделеева – Клапейрона.

pV = ϑRT =(m/μ)RT (pμ)/RT=m/V=ρ

Если имеется смесь газов, то малярная масса измеряется как средневзвешенная μ= + …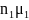

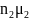n- мольные доли данных газов.

Мольные доли - способ выражения концентрации( определенное количество молей данного газа в 1-м моле смеси)

• Давление - сила действующая на единицу площади Р=F/S

• Вязкость жидкости- μ(динамическая вязкость), ϑ(кинематическая вязкость)

ϑ = μ/ρ

Силы вязкости в жидкости связаны с механическим притяжением в жидкости, поэтому сдвиг в слое жидкости относительно другого слоя связан с разрывом межмолекулярных связей и происходит с затратами энергии. Из-за затруднения движения слоёв внутри жидкости вязкость называют ВНУТРЕННИМ ТРЕНИЕМ. Вязкость проявляется лишь тогда, когда жидкость движется, и при этом внутри нее имеются слои с разной скоростью движения. Появление этих слоев всегда связано с наличием неподвижной твердой стенки, смачиваемой жидкостью.

Взаимодействие движущейся жидкости с твердой стенкой или каким - либо объектом, находящимся внутри жидкости и движущимся с другой скоростью приводит к появлению силы сопротивления. Сила сопротивления зависит от отношения скорости движения стенки (объекта) и жидкости. Сила сопротивления описывается законом Ньютона Н = -μ Ḟ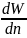

Ḟ-площадь поверхности (const)

H-сила сопротивления

Направление n нормально по отношению к стенке или объекту. Профиль распределяет скорость внутри жидкости,текущей в трубе со смоченными стенками.

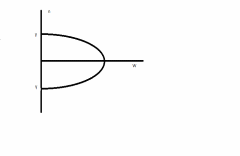Из графика видно, что в пристеночной области скорость жидкости равна нулю, а в центре потока достигает максимального значения.

Такой профиль характерен для ламинарного потока жидкости. Другой вариант течения – турбулентный. Он возможен при более высокой скорости и характерен тем, что взаимодействие между движущимеся слоями жидкости приводит к тому, что появляются вихри, жидкость закручивается и выравнивается. Турбулентное движение требует больших затрат энерегии на закручивание вихрей. Затраты обеспечивают превосходное перемешивание внутри потока жидкости.

Из уравнения Ньютона следует, что μ = [

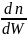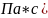
• Повехностное натяжение

Это свойство так же связано с межмолекулярным притяжением. Поверхностное натяжение характеризует энергию, которую необходимо приложить к жидкости для разрыва межмолекуляных связей и образования одной единицы площади поверхности.

Ϭ[дж/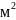 ] – поверхностное натяжение.

• Скрытая энтальпия парообразования.

Наличие ее так же связано с межатомным натяжением. Обозначается как ∆Н.

Бывает так же скрытая теплота парообразования. Обозначается как ∆Q, численно равная ∆Н, но с обратным знаком.

Эти велечины отображают энергию, которую необходимо затратить для полного разрыва одного моля жидкости и перевода этого моля в идеальное газовое состояние (т.е. без механического взаимодействия).

Размерность ∆Н и ∆Q – Дж/моль.

Основное уравнение гидростатики.

В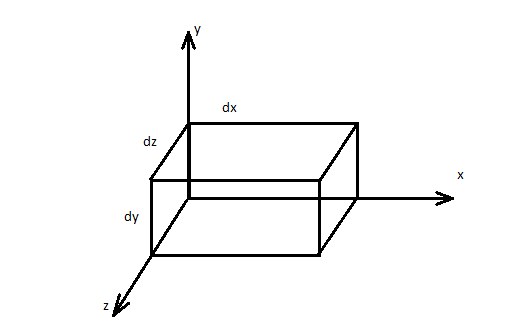 толще неподвижной жидкости выделим элементарны параллелепипед, который в трехмерном пространстве xyz имеет длину граней dx,dy,dz. Пусть по оси z на ближнюю грань оказывается давление Р. Тогда Р = Ṗ/dxdy. Ṗ = P*dxdy. На дальнюю грань в этом же напралении оказывается давление 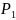, поэтому эта грань удалена от ближних граней на расстояние dz, тогда прирост давления на дальнюю грань 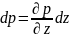. Здесь частные производные 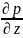характеризуют физическую зависимость давления от постоянной. Тогда сила давления на данной прлощади будет .

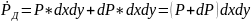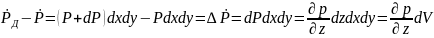По направлению “x” рассуждения будут аналогичны

=

=

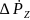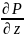
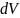
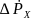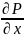
Для направления “y” к рассматривамой силе прибавится сила тяжести, т.е.

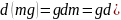, тогда

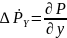
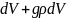
Поскольку жидкость ститическая,то равнодействующая всех сил равна 0, тогда

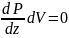
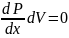
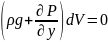
так как

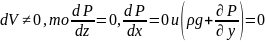
[система уранений Эйлера для неподвижных жидкостей]

Поскольку изменение давления по осям “z ” “x” нет,то рассмотрим направление “y”

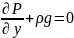
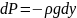
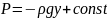
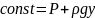
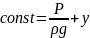
Длину по оси “y” примем за высоту столба и назовем его геометрическим напором Н. Частное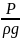 назовем статическим напором. Сумма ститическиго и геометрического напора есть величина не постоянная. Тогда

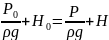
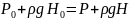
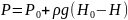- основной закон гидростатики или закон Пекаля.

Уравнение отражает зависимость давления внутри столба жидкости в зависимости от высоты подъема по сравнению с 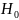. Оно отражает зависимость статического давления от геометрического напора:

Если H растет, то Р убывает.

Если

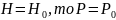
В точке, где статический напор максимален - геометрический напор равен нулю и наоборот.

П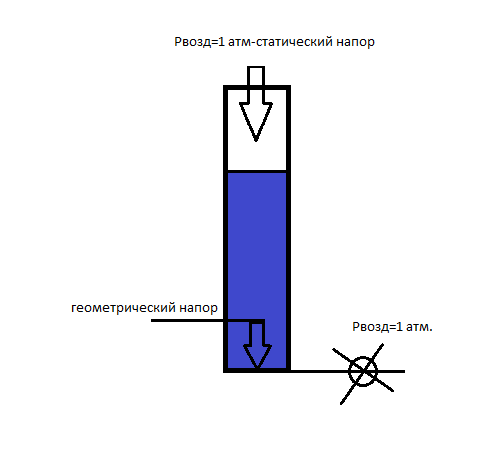 ока кран закрыт,на дно давит статический и геометрический напор. Эта система не подчиняется закону Паекаля.

Если кран открыт,то внизу также появляется Рстат=1атм. Такая система подчиняется закону Паекаля.

Если кран открыт,то статический напор давит и на выход из крана, и на врехушку столба жидкости, поэтому эти 2 напора компенсированы и жидкость течет только под геометричеким напором. В это случае в верхней части столба геометричаский напор=0,а статический максимален. В нижней части наоборот.

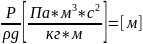Напор-давление,выраженное в метрах жидкостного столба.