Лекция СПСС

29.11.2012

Вопросы к экзамену = "Рабочие материалы для подготовки к экзамену по дисциплине"

Одномерный анализ номинальных и порядковых шкал

1. БД «ВАО». Используя процедуру частотного распределения по переменной В.2, определите: сколько процентов избирателей ВАО не пойдет на выборы 4 декабря. Построй круговую диаграмму.

бд из "бд к экз" вао1500

частотный, одномерный анализ

два раза клик на диаграмму - редактор диаграмм

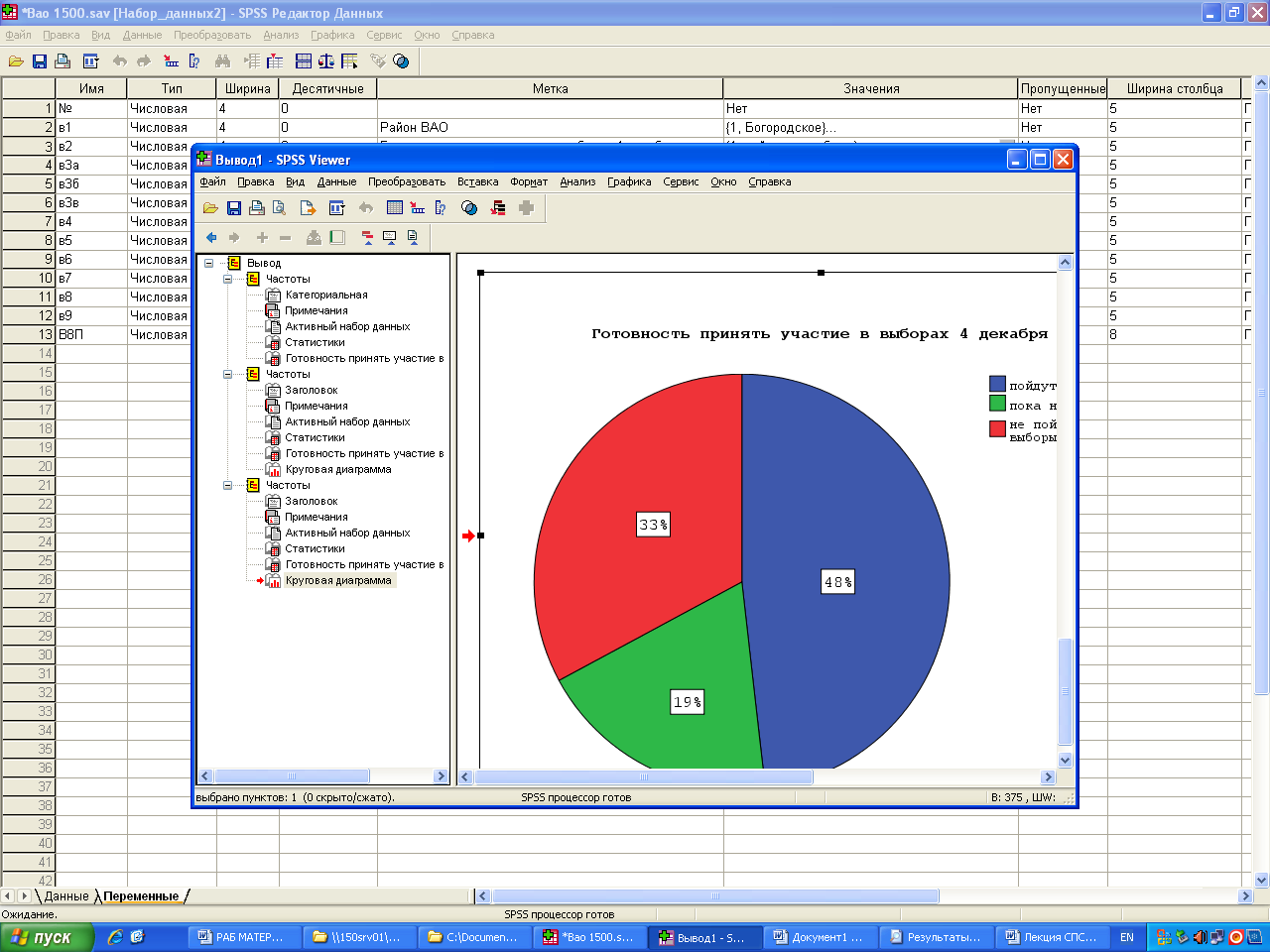
Таблицу, которую мы берем их СПСС надо отформатировать прежде чем использовать ее в отчетах или в научной работе.

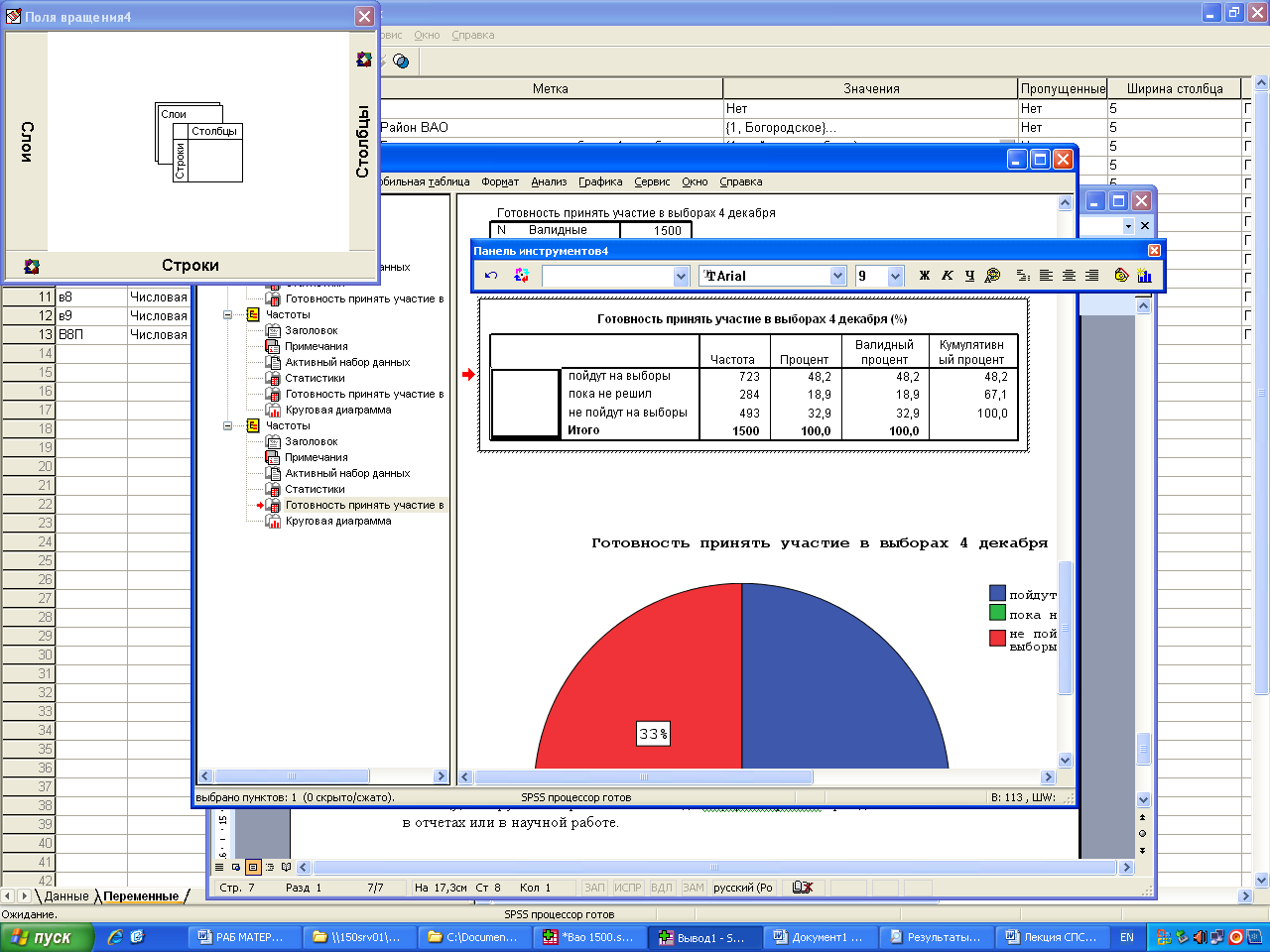
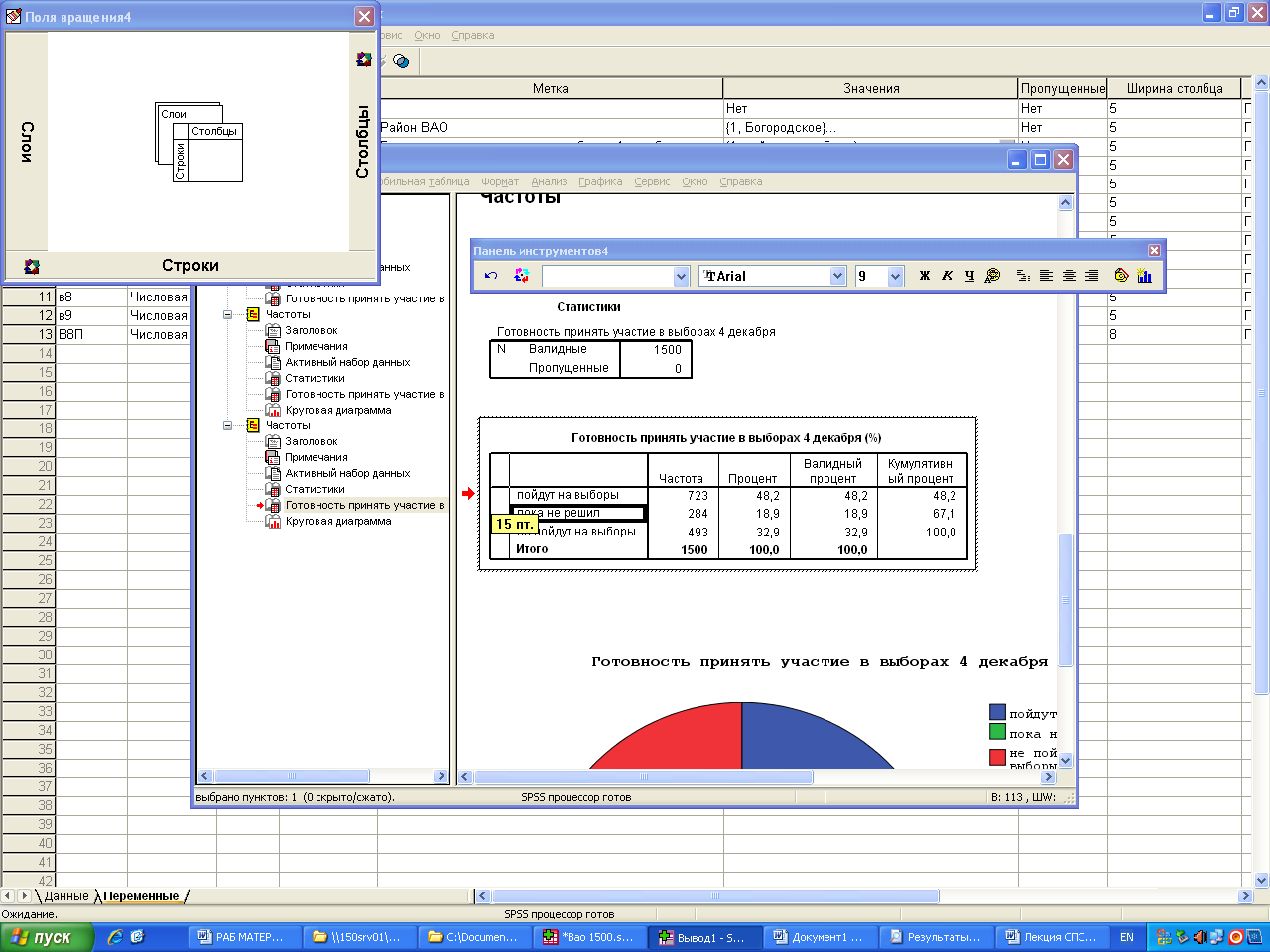
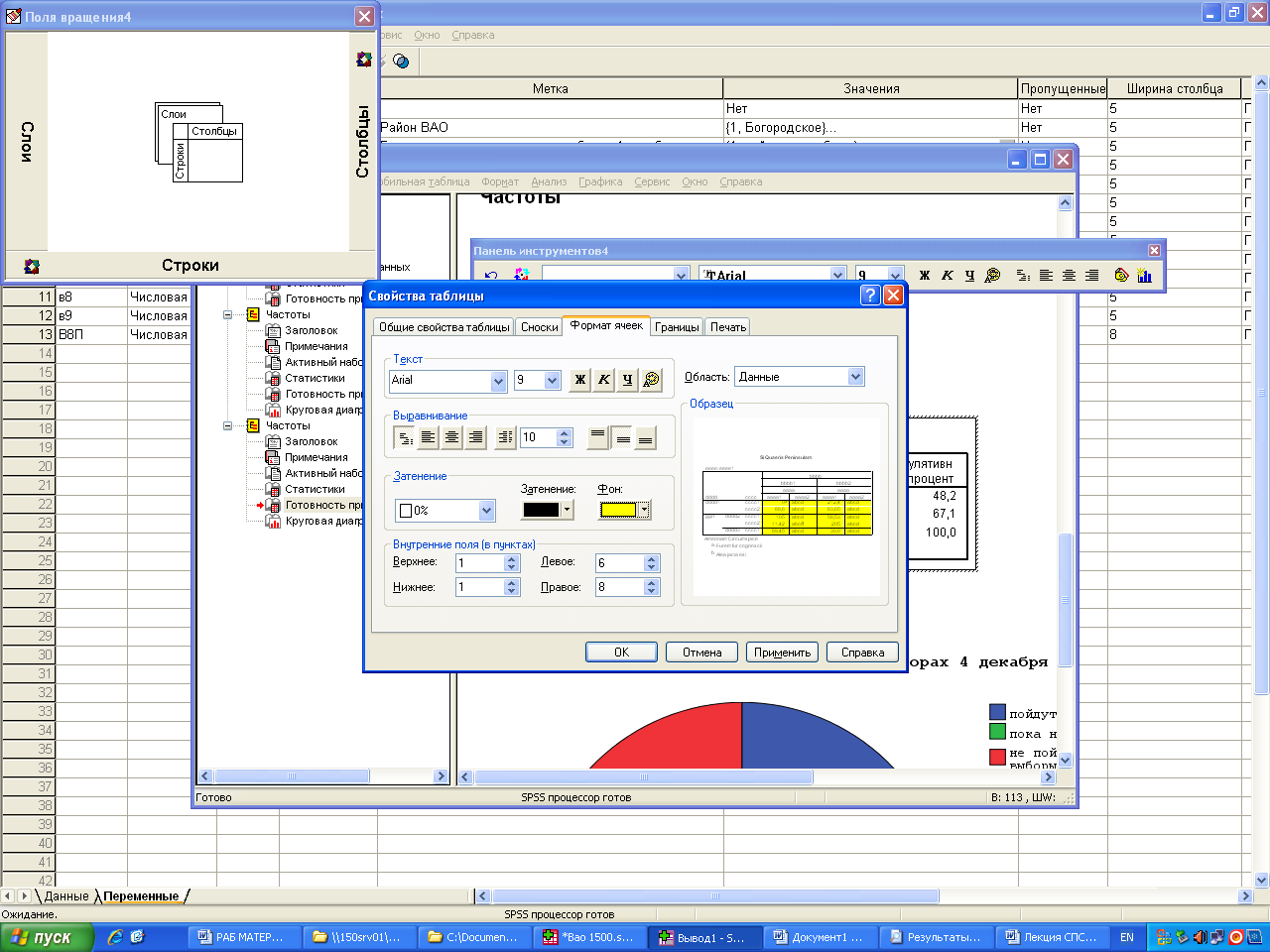
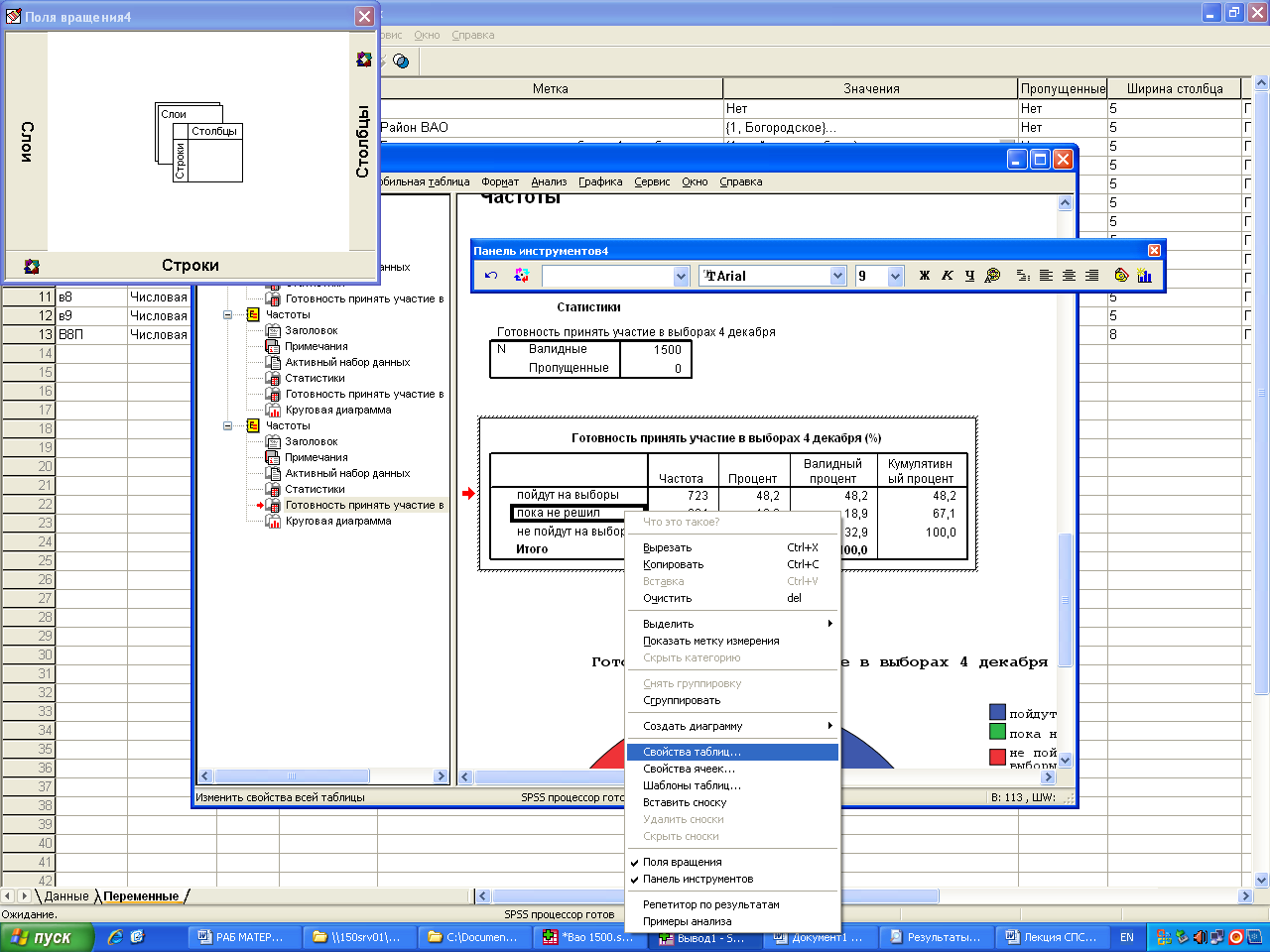
Процент – количество ответивших

Валидный процент – количество опрошенных

Данные в ср арифм значениях, а нам надо проценты. Но как эти значения были сформированы? Да =1

Если *100 – будут проценты

_ _

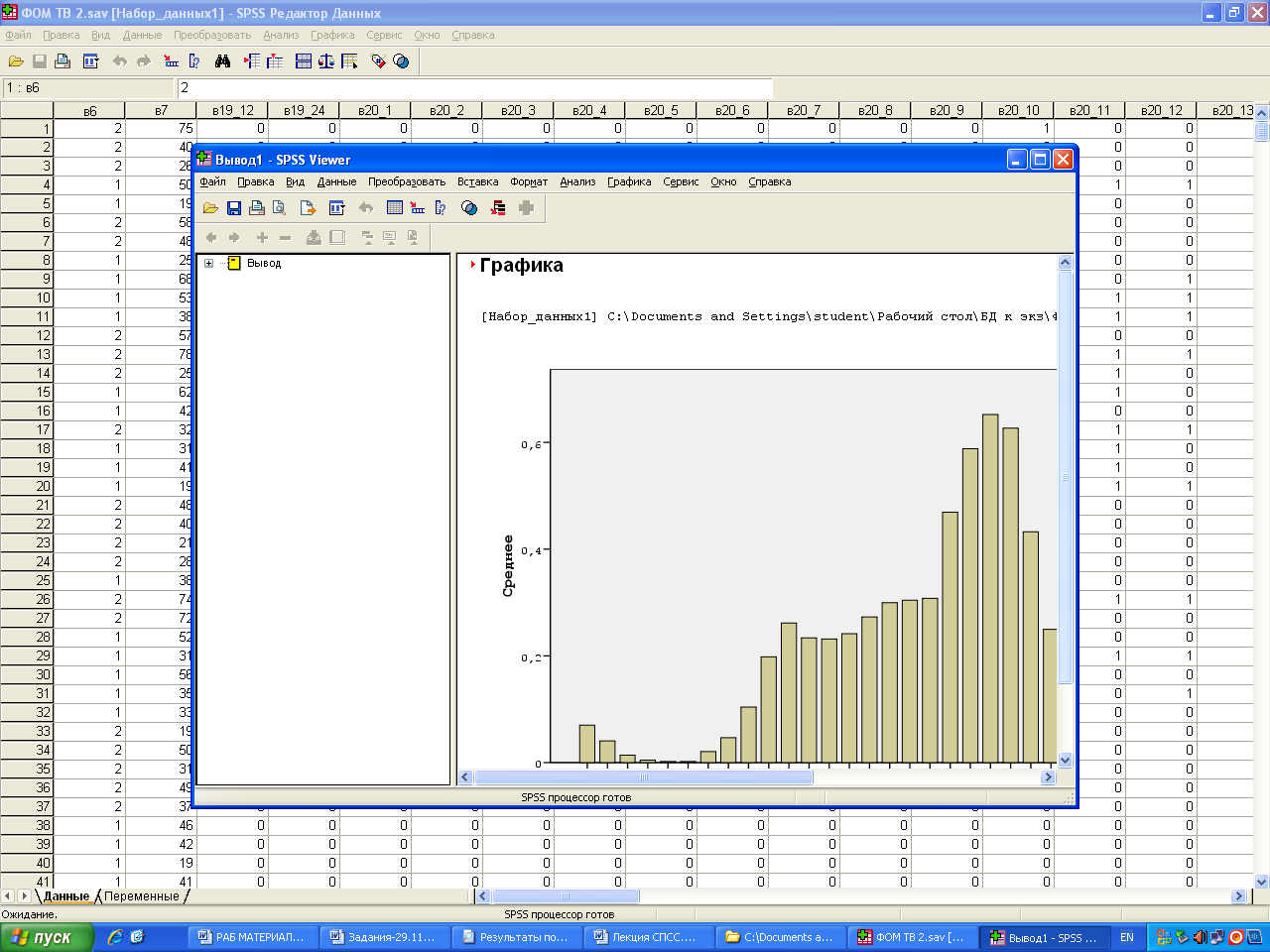
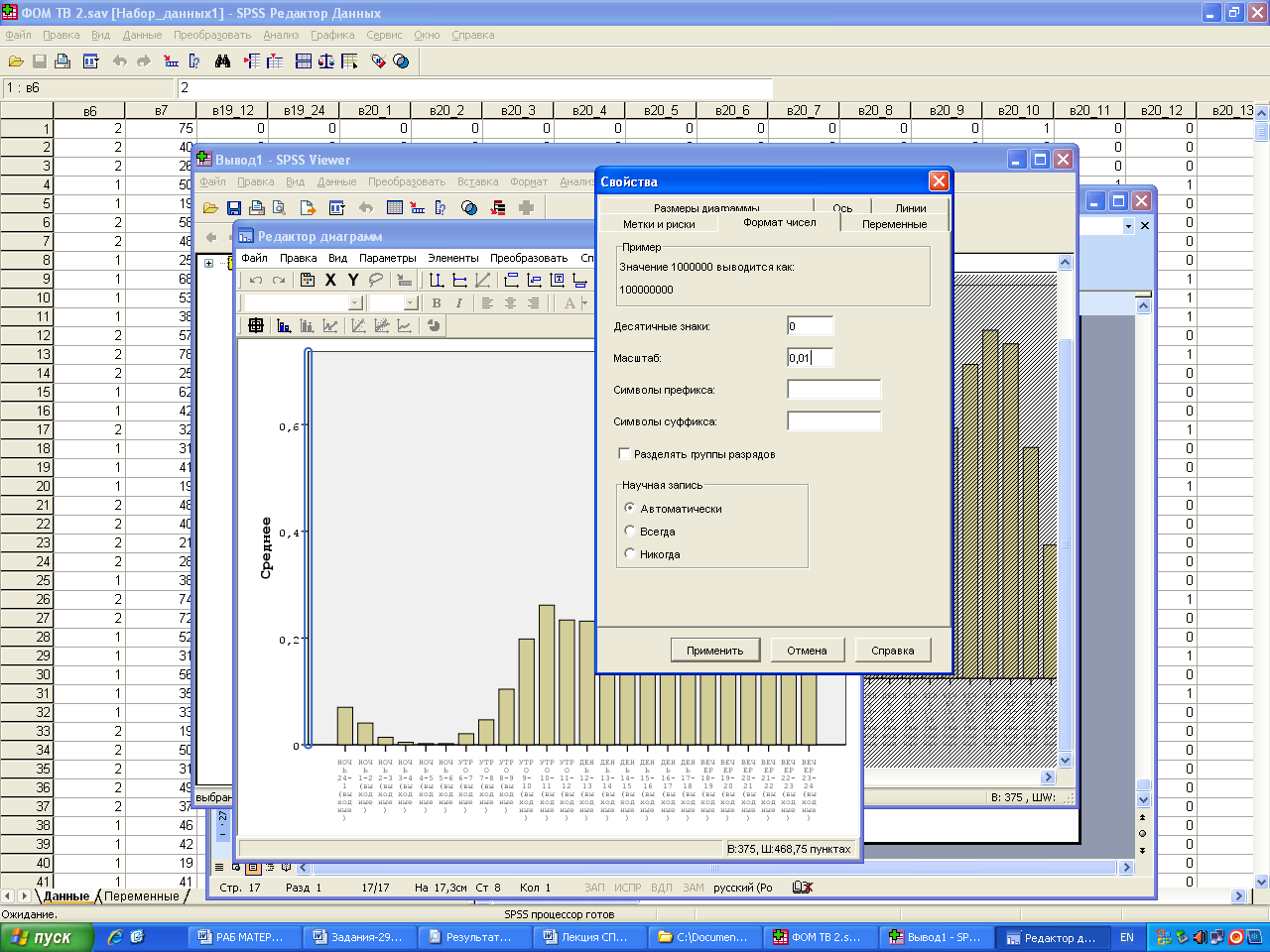
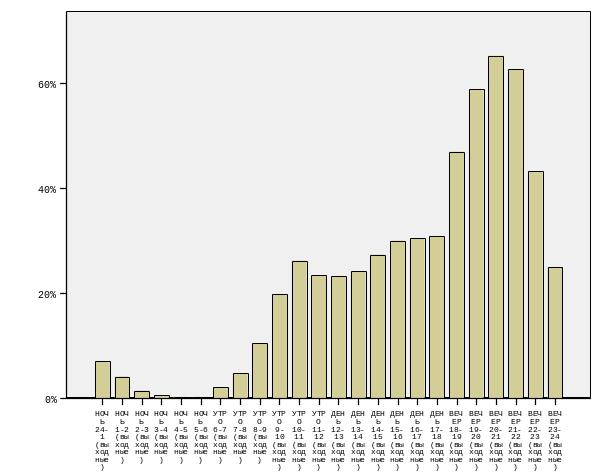ВАО

(восточный административный округ)

Номинальные шкалы – это просто имена (спортсмены, не означает победителя)

Порядковые шкалы – упорядоченная

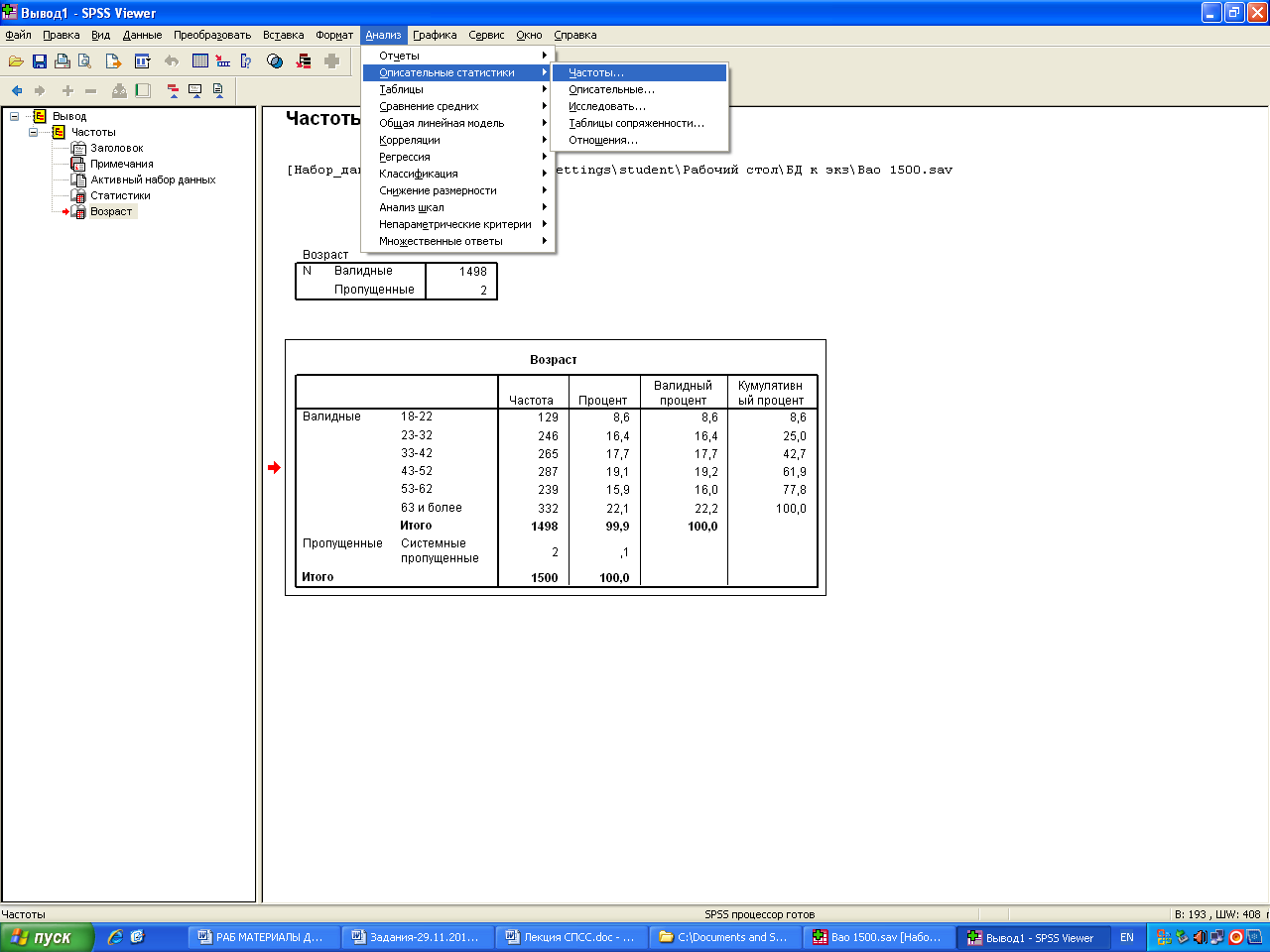
Кумулятивный процент

Возраст

		Частота	Процент	Валидный процент	Кумулятивный процент
Валидные	18-22	129	8,6	8,6	8,6
	23-32	246	16,4	16,4	25,0
	33-42	265	17,7	17,7	42,7
	43-52	287	19,1	19,2	61,9
	53-62	239	15,9	16,0	77,8
	63 и более	332	22,1	22,2	100,0
	Итого	1498	99,9	100,0
Пропущенные	Системные пропущенные	2	,1
Итого		1500	100,0

Валидный процент

8,6

16,4

17,7

19,2

16,0

22,2

Прибавляем одно к другому, последовательно

Получается

Кумулятивный процент

8,6

25,0

42,7

61,9

77,8

100,0

!!! Но это имеет смысл только для порядковых шкал!!!

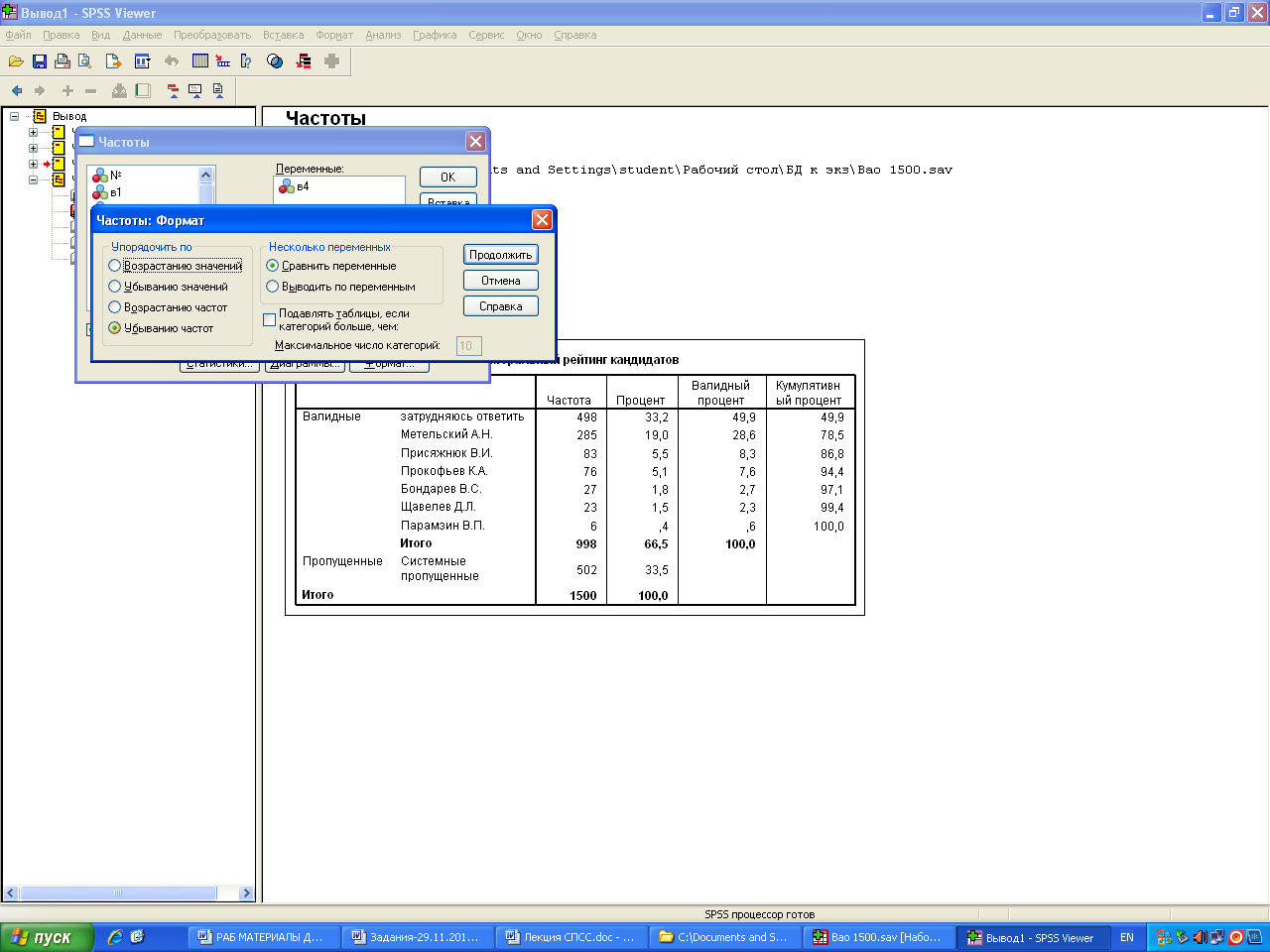
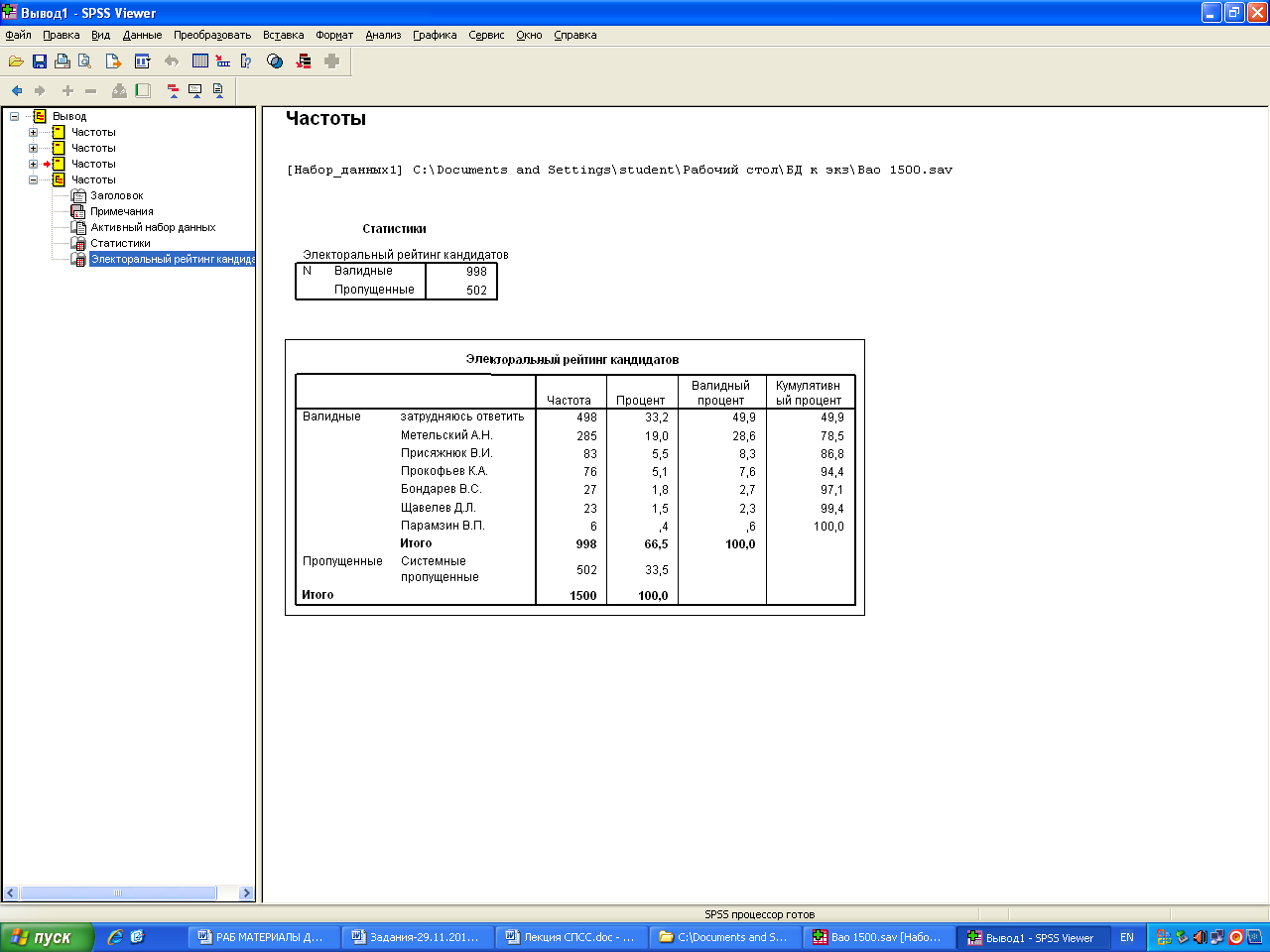
Те, кто затрудняется ответить, будут склоняться скорее всего к тому, за кого больше всего голосуют.

Количественный тип переменной – интервальная шкала

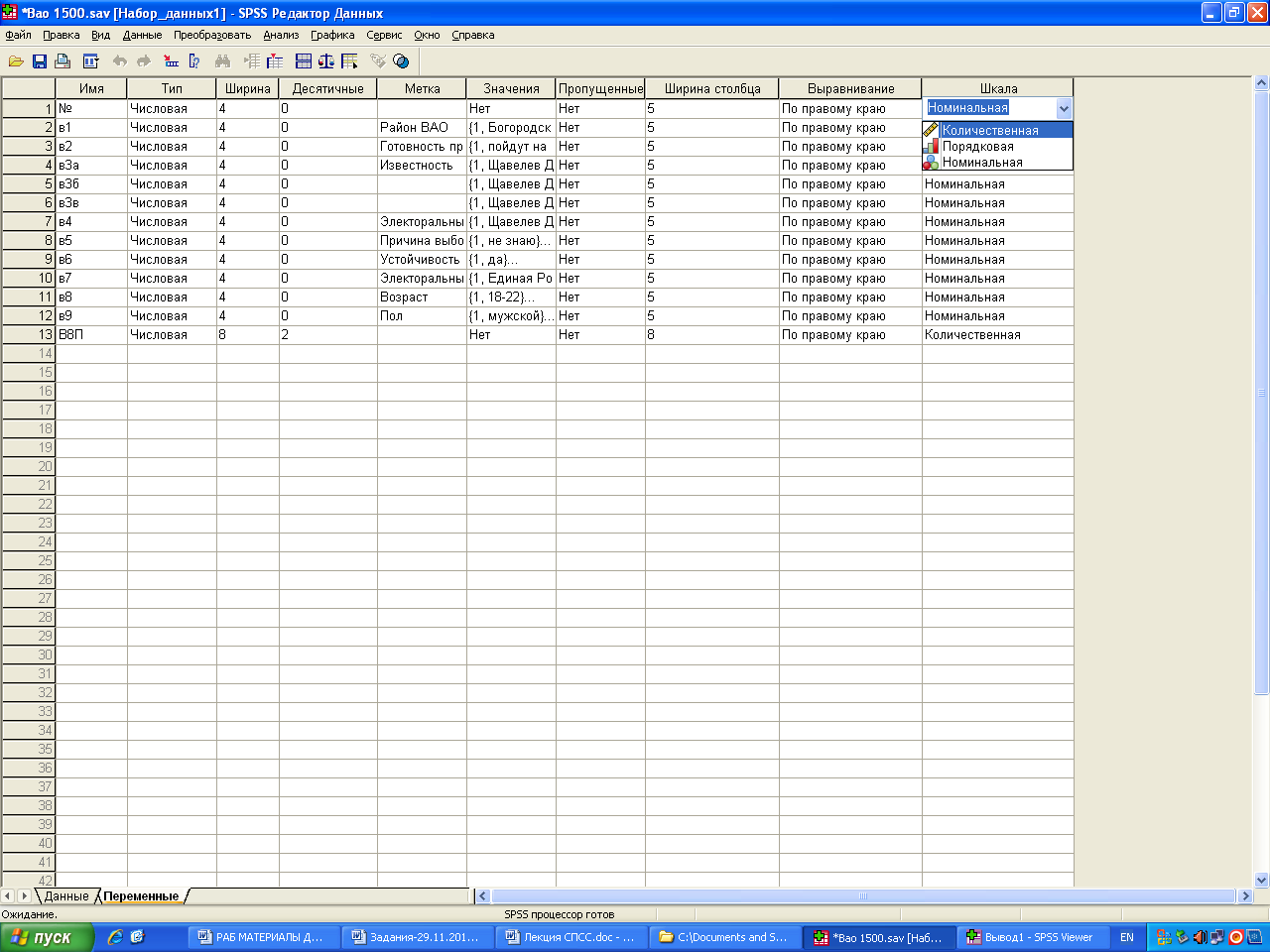
Кнопочка «статистики» когда будем говорить о количественных переменных

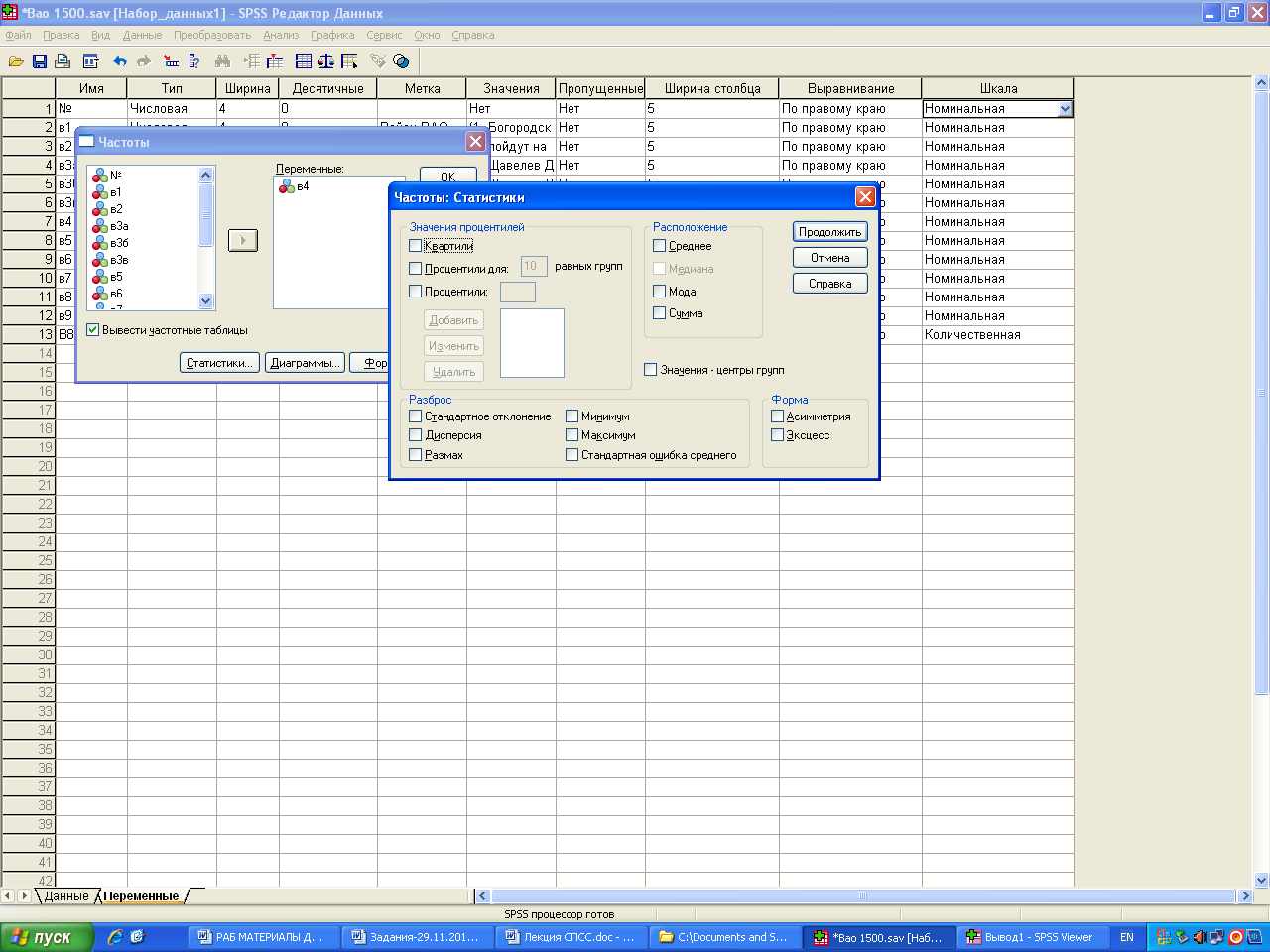
Качественные: номинальные описывает характеристики

Количественные: позволяют сравнить переменные (насколько одна больше другой)

Л4 Одномерный анализ количественных переменных

Две группы статистических характеристик распределения переменных:

• Показатели центра распределения

- мода

- среднее арифметическое

- медиана

Для количественных (все)

Для качественных: номинальные и порядковые (медиана, мода, нельзя среднее арифметическое) вместе

Для порядковых (медиана, мода, нельзя среднее арифметическое)

Для номинальных (мода)

Если значение встречается чаще всего (1 Единая Россия), значит оно называется модальным.

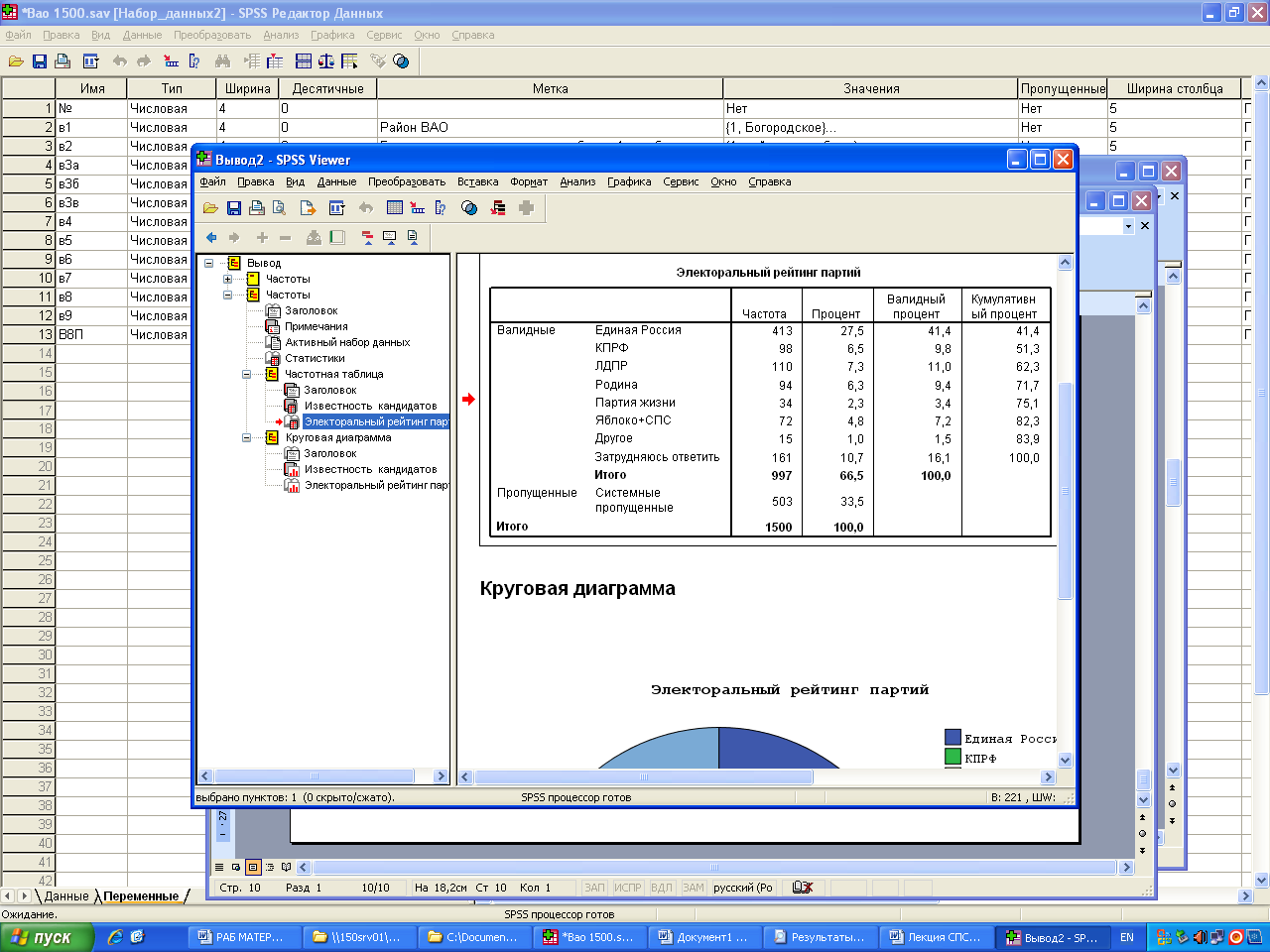
Электоральный рейтинг партий

		Частота	Процент	Валидный процент	Кумулятивный процент
Валидные	Единая Россия	413	27,5	41,4	41,4
	Затрудняюсь ответить	161	10,7	16,1	57,6
	ЛДПР	110	7,3	11,0	68,6
	КПРФ	98	6,5	9,8	78,4
	Родина	94	6,3	9,4	87,9
	Яблоко+СПС	72	4,8	7,2	95,1
	Партия жизни	34	2,3	3,4	98,5
	Другое	15	1,0	1,5	100,0
	Итого	997	66,5	100,0
Пропущенные	Системные пропущенные	503	33,5
Итого		1500	100,0

Модальное – наиболее часто встречающееся значение (типичное)

Медиана – значение, которое делит распределение пополам, на две части

=Среднее значение в упорядоченном ряду

Рекомендуется использовать, когда есть большие выбросы, потому что оно сильно искажает среднее арифметическое (больница, средняя температура по земле).

Такие техники все равно используются дл того, чтобы отразить средние показатели исследуемого объекта. Но надо чтобы эти показатели были адекватными.