3. Синтез компенсатора
Если на систему управления неучтенное при синтезе возмущение F(t), то для ослабления их влияния на поведение системы необходимо принять дополнительные меры. В частности, если на объект управления действует контролируемое возмущение, то для его устранения используют принцип компенсации возмущения. Зaдача синтеза сводиться к определению алгоритма блока компенсатора, который может обеспечить абсолютную инвариантность управляемого параметра к контролируемому воздействию.
На практике на автоматическую систему могут оказывать влияние внешние воздействия различные по своей природе, которые изменяют регулируемую величину сигнала на выходе и ухудшают управляемость системой.
Для того, чтобы добиться желаемого качества процесса управления или регулирования (требуемой точности системы и качества переходного процесса), можно изменить структуру системы, введя дополнительные звенья – корректирующие устройства (компенсаторы).
Основная задача компенсаторов состоит в улучшении точности системы и качества переходных процессов.
Систему с компенсатором в общем виде можно представить:
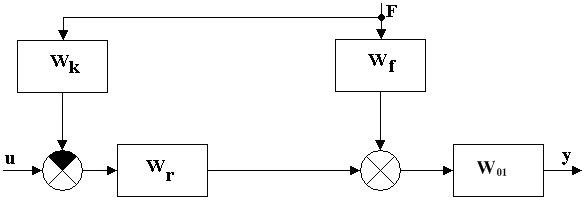
Рис. 3.1 Система с компенсатором
Для расчета передаточной функции компенсатора используем следующий алгоритм:
Для нахождения компенсатора будем использовать пакет Matlab:
clc,clear % очистка экрана и реестра
w=0:0.01:10; % задание шага частоты
s=i*w; % переход в частотную область
Kd=8.35; % D составляющая регулятора
Kp=0.12; % P составляющая регулятора
Ki=0.000449; % I составляющая регулятора
Wff=tf([0.4],[10 1]); % Задаем возмущение
Wrrr=tf([Kd Kp],[ 1]) % задаем Kp и Kd
Wrr=tf([Ki],[1 0]); % задаем интегральный коэффициент регулятора
Wreg=Wrr+Wrrr % передаточная функция решулятора
8.35 s^2 + 0.12 s + 0.000449
----------------------------
s
Wk=Wff*(Wrr+Wrrr)^(-1) % передаточная функция компенсатора
0.4 s
-----------------------------------------
83.5 s^3 + 9.55 s^2 + 0.1245 s + 0.000449
Условие физической реализуемости компенсатора соблюдено – степень числителя не превышает степень знаменателя.
Моделируем работу системы по каналу возмущения с компенсатором в Simulink. Для этого на вход системы подаем 0, а на вход канала возмущения подаем единичный ступенчатый сигнал равный 1. Полученный график сравниваем с аналогичным для системы без компенсатора, и делаем выводы о его влиянии на процессы в системе.
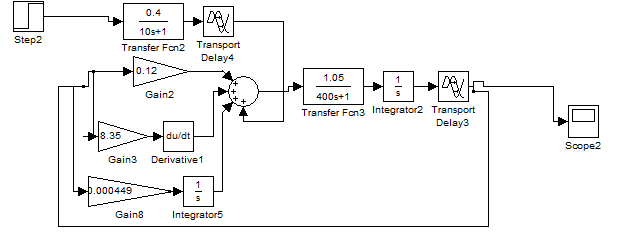
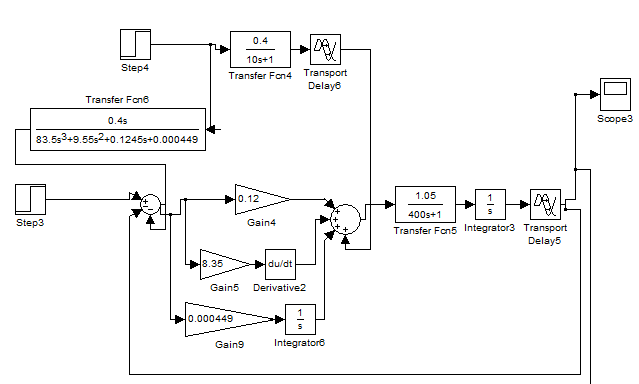
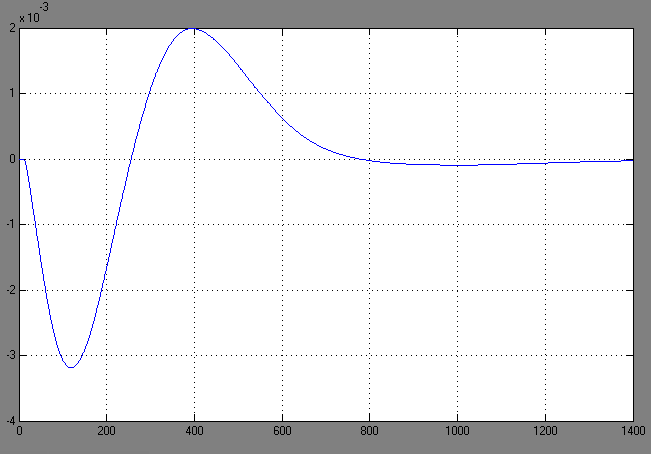
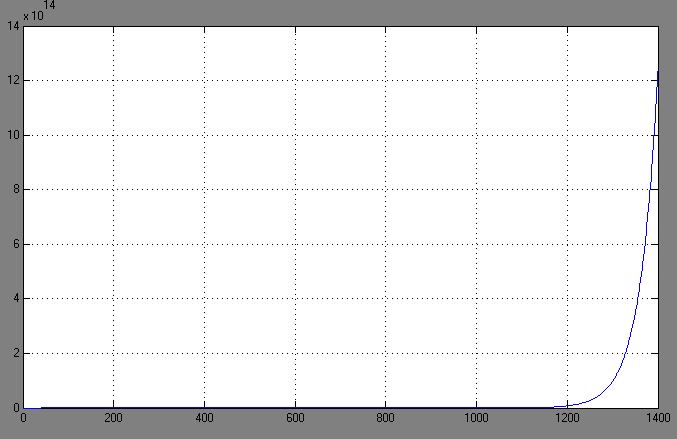
а) б)
Рис.3.2 Поведение системы с учетом возмущения при применении компенсатора (а)) и без него (б))
Как мы видим из графиков, ввод в систему корректирующего звена (компенсатора) уменьшает влияние возмущения, а именно почти сразу убирает возмущение( погрешность менее 0.4%)
Итак, рассчитанный мною компенсатор устраняет возмущение почти идеально.