Глава 3 метод гілок та меж

3.1 Основні поняття

Цей метод буде застосовано для розв’язання задачі про рюкзак та задачі комівояжера.

Сформулюємо основні ідеї метода гілок та меж.

Деяка функція має бути мінімізована f(x)→min, де Х складається з дискретних точок (наприклад, цілочисельних). Це задача нелінійного програмування, навіть якщо f(x) – лінійна функція.

Якщо множина Х складається з невеликої кількості елементів, то можливий перебір всіх елементів, якщо кількість елементів множини Х є великою, то потрібен метод спрямованого перебору. Одним з таких методів є метод гілок та меж . В цьому методі треба вказати дві речі:

1. алгоритм розбиття множини Х;

2. деяку систему оцінок будь-якої підмножини Х.

Множину Х розбиваємо на дві – три частини

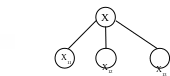
Х_11, Х_12, Х₁₃ – кінцеві множини 1-го кроку.

На другому кроці за деякою ознакою вибираємо одну з множин 1-го кроку і розбиваємо її. Одержані множини разом з нерОзгалуженими множинами другого кроку називаються кінцевими множинами другого кроку.

Для системи оцінок множин запроваджується функція ρ(Х^*), Ця функція повинна задовольняти наступним вимогам:

1. оцінка будь-якої підмножини ρ(Х^*) при розбиті повинна бути меншою, ніж min f(x), ;

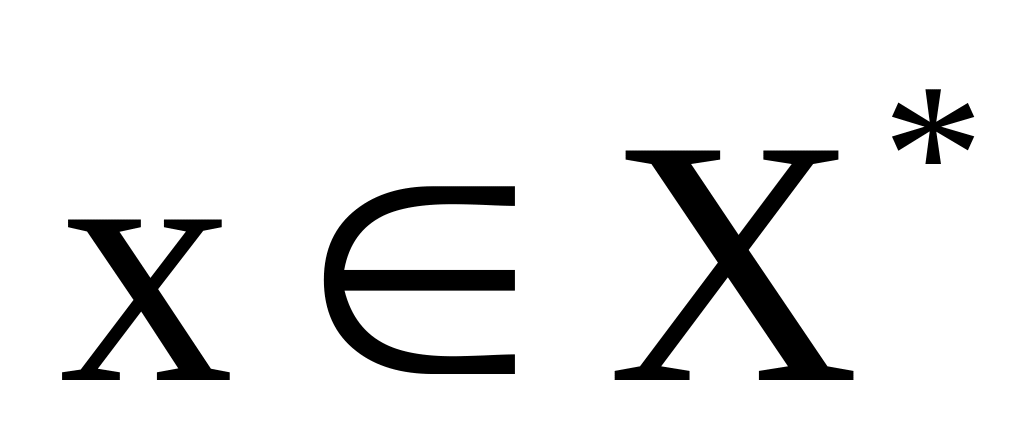2. оцінка будь-якої підмножини повинна бути меншою за оцінку тієї множини, з якої ця підмножина одержана, тобто ρ(Х^*) ≥ ρ(Х), ;

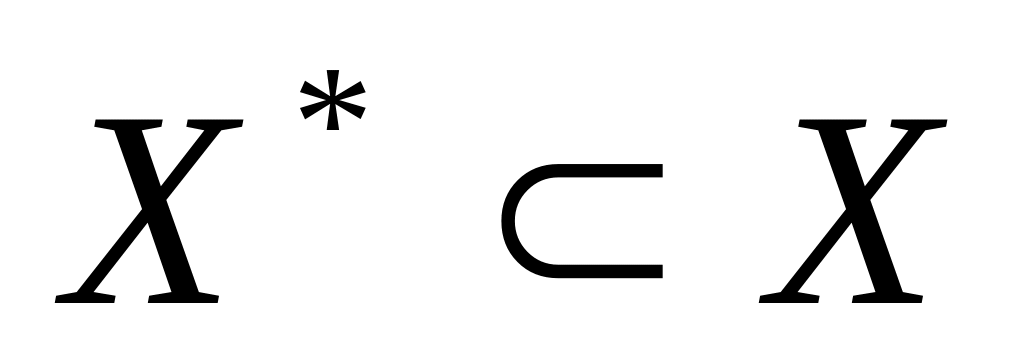з цього випливає, що при розбитті оцінка ρ(Х) не може спадати;

3. оцінка множини, що складається з однієї точки, дорівнює значенню цільової функції f(x) в цій точці.

Ми розглянемо реалізацію метода гілок та меж, яка називається повне галуження.

Для цього на першому кроці обчисляємо оцінку множини Х − ρ(Х) за означеним правилом. Після цього обчислюється оцінка ρ для підмножин Х₁₁, Х₁₂. Зі знайдених оцінок ρ(Х₁₁), ρ(Х₁₂) обирається найменша, і далі галузиться та множина, для якої оцінка ρ найменша. Після цього процедура повторюється.

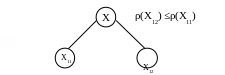
Далі галузимо ρ(Х₁₂):

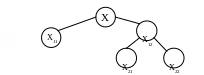
З трьох множин Х_11, Х_21, Х₂₂ вибираємо ту, для якої оцінка є найменшою. Галузимо доти, поки не доберемося до множини, що складається з однієї

точки, оцінок кінцевих множин останнього кроку.

3.2 Задача про рюкзак

Є n предметів. Відомі вага p кожного i вартість c , i = . Потрібно покласти у рюкзак сукупність предметів з мінімальною сумарною вагою за умови, що вартість вантажу не менша за С. Введемо в розгляд змінну :

Тоді одержуємо задачу:

Це повна постановка задачі про рюкзак. Опишемо алгоритм галуження i зв'язану з ним систему оцінок. Для того, щоб обчислити оцінку ρ(х), треба розв’язати задачу лінійного програмування (неперервну), тобто розв’язуємо свою задачу, але умову замінимо на 0 ≤ х_і ≤ 1. Таким чином

ρ(х) =min f(x) за умови 0 ≤ х_і ≤ 1. За умови 0 ≤ х_і ≤ 1 min f(x) може тільки зменшитися, тобто ρ(x) ≤ minf (x), і вимога на ρ(х) виконана.

Складаємо відношення – це відносна вага предмета на одиницю вартості. В першу чергу будемо класти в рюкзак ті предмети, що мають min . Умова 0 ≤ х_і ≤ 1 означає, що маємо право дробити предмети. При цьому множина припустимих значень збільшується, a min функції може лише зменшуватися.

Приклад. Маємо п’ять предметів, які треба покласти в рюкзак за умови, що вартість предметів у рюкзаку

і	1	2	3	4	5	С=30
сі	10	5	16	4	6	вартість
рі	6	2	5	8	4	Вага

Математична модель задачі така: ми шукаємо min ваги

f(x) = 6х₁ + 2х₂ + 5x₃ + 8х₄ +4х₅ → min

за умови, що вартість вантажу

10х₁ + 5x₂ + l 6x₃ + 4x₄ + 6x₅≥ 30. (1)

Коли задача буде розв'язана, ми одержимо такий граф-дерево:

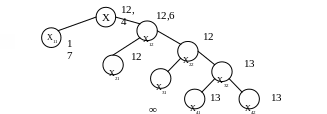
Зробимо оцінку планів задачі (1), тобто будуємо оцінку ρ.

(2)

Це задача (2) лінійного програмування. Розв'яжемо її.

Розташовуємо предмети в порядку зростання i відповідно перенумеруємо предмети.

і	1	2	3	4	5
поперед. ном.	3	2	1	5	4
сі	16	5	10	6	4
рі	5	2	6	4	8

Задача (2) тоді має вигляд (з новою нумерацією предметів):

Якщо візьмемо перший предмет, тоді його вартість 16<30; якщо перший і другий, то їх вартість 16+5=21<30. Якщо візьмемо перший, другий і третій предмети, то їх вартість буде 16 + 5 + 10=31, 31 > 30 на одиницю. Яку частину третього предмета треба взяти? Одиниця – це вартості третього предмета, тобто треба взяти предмета. Тоді опорний план задачі (2): (1; 1; 0,9; 0; 0); ρ(х) = 5 + 2 + б*0,9 = 12,4.

Будемо галузити множину опорних планів по третій координаті, оскільки вона не ціла. Розбиваємо множину Х, тобто сукупність планів задачі (2),на дві підмножини.

З’являються задачі (3) і (4):

(3)

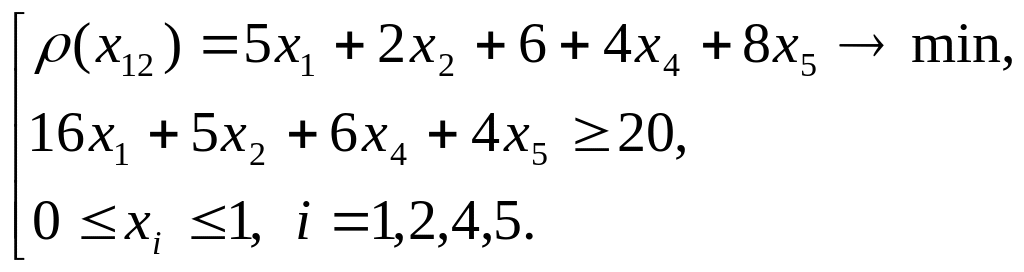(4)

Для задачі (3) третього предмета немає.

1пр. + 2пр. + 4пр. 16 + 5 + 6 = 27 < 30,

1пр. + 2пр. + 4пр.+ 5пр. 16 + 5 + 6 + 4 = 31 > 30.

П’ятий предмет перевищує вартість на одиницю, тобто на 1/4 його вартості, тоді потрібно взяти 3/4 п’ятого предмета. Опорний план для задачі (3) наступний: (1; 1; 0; 1; 3/4),

ρ(х₁₁) = 5 + 2 + 4 + 8*(3/4) = 17.

Розв’язуємо задачу (4):

1 пр. + 2 пр. 16 + 5 = 21>20.

Вже другий предмет перевищує вартість на одиницю, тобто на 1/5 його вартості; треба взяти 4/5 другого предмета. Опорний план (1;4/5, 1; 0; 0),

ρ(х₁₂)= 5 + 2*(4/5)+6+0=12,6.

Із ρ(х₁₁) i ρ(х₁₂) вибираємо min, це ρ(х₁₂), і далі галузимо х₁₂ за другою координатою:

З'являються задачі (5) i (6):

(5)

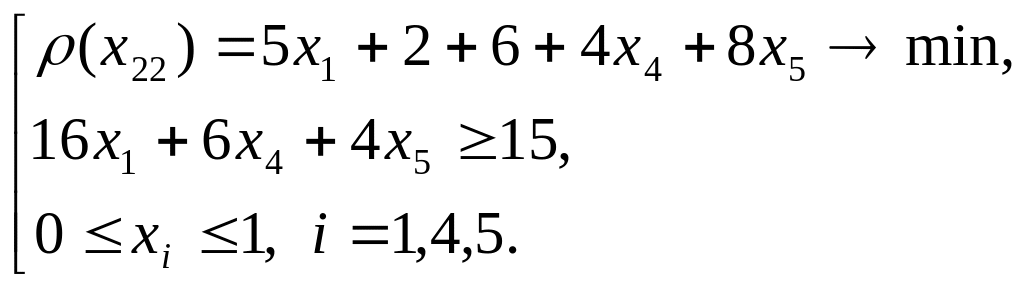(6)

Розв’язуємо задачу (5).

1 пр.+ 4 пр. 16 + 6 = 22 > 20. Четвертий предмет перевищує вартість на 2 одиниці або на його вартості, тобто потрібно взяти четвертого предмету. Опорний план такий: (1; 0; 1; ;0),

ρ (х₂₁) = 5+6+4* =13 .

Розв’язуємо задачу (6).

1 пр. 16 > 15. Перший предмет перевищує вартість на 1 одиницю, тобто на своєї вартості треба взяти від першого предмету. Опорний план (6) задачі ( ; 1; 1; 0: 0), ρ(х_2,2) =5* + 2 + 6 = 8 + = 12 .

Кінцеві множини цього кроку X₁₁, Х₂₁, Х₂₂

min ρ = ρ(X₂₂) = l2 .

Далі треба галузити Х₂₂ за першою координатою:

Задачі (7) i (8):

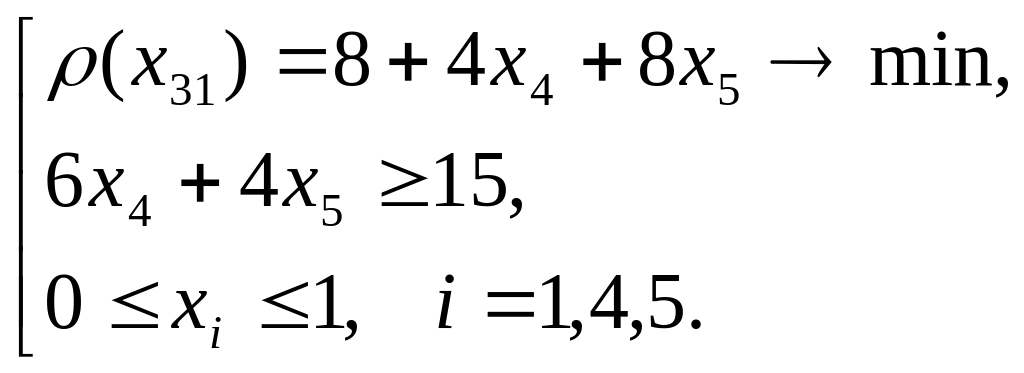(7)

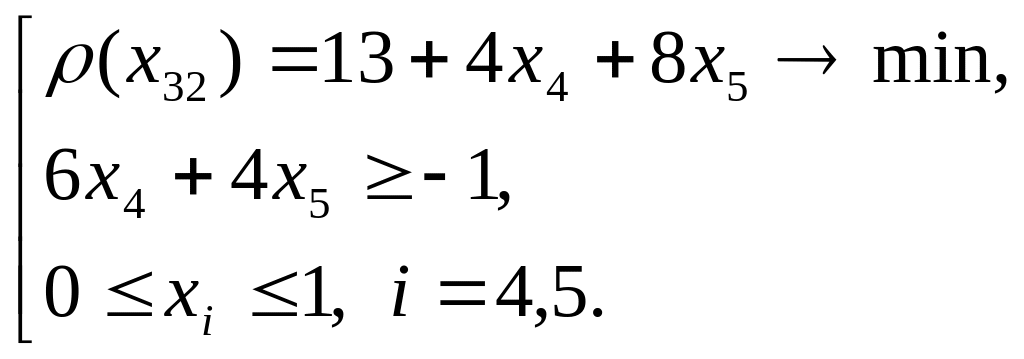(8)

Розв’яжемо задачу (7).

4пр.+5 пр. с=10<15 множина планів порожня. Тоді відповідну оцінку вважаємо рівною ∞, тобто ρ(X₃₁) = ∞. Така множина галуженню не підлягає.

Розв’язуємо задачу (8). Розв'язок цієї задачі (1;1; 1; 0; 0), ρ(X₃₂) = 13.

Кінцеві множини третього кроку Х₁₁, X₂₁, X₃₁, X₃₂; min ρ = ρ(X_3,2) = l3.

План задачі (8) цілочисельний, тому множина Х_3,2 розбивається таким чином: одноелементна підмножина Х_4,1 = {1,1,1,0,0} – одна точка, i X_4,2=X_3,2\X_4,1. Вважаємо при цьому ρ(Х_4,1) = ρ(Х_4,2) =ρ(Х_3,2) =13. Елемент Х_4,1 є розв'язком задачі.

Оптимальне значення цільової функції 13. Якщо перейти до старої

нумерації, тоді в рюкзак треба покласти 3,2 і 1 предмети.