5.4 Геометрична інтерпретація гри

Розв’язання гри допускає наглядну геометричну інтерпретацію. Запишемо платіжну матрицю цієї гри:

.

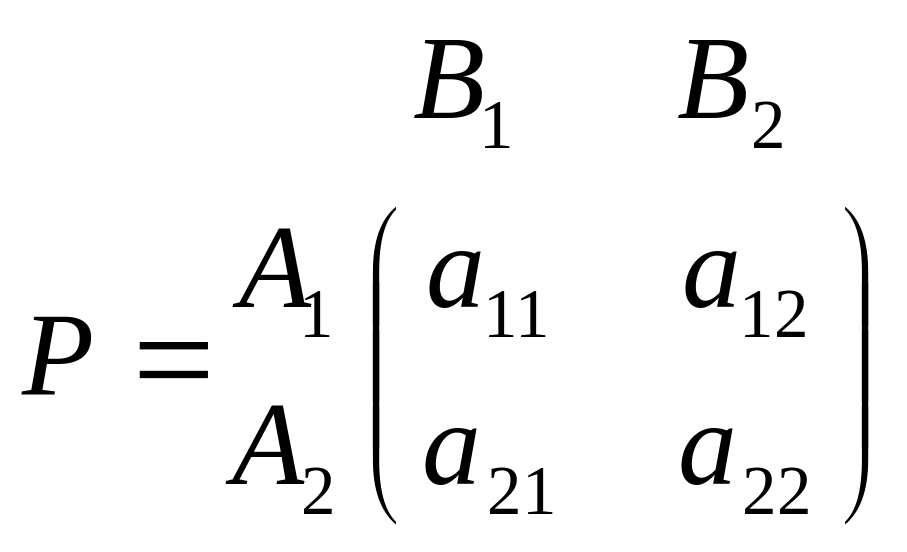Мішані стратегії гравців

.

За теоремою 2 маємо:

,

.

З точки зору геометрії маємо рівняння двох прямих в системі координат (p,v):

v = a₁₁ p + a₂₁ (1–p),

v = a₁₂ p + a₂₂ (1–p).

Побудуємо графіки цих прямих.

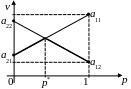
Гравець А розраховує на min(F(S_A,B₁), F(S_A,B₁)) – жирно виділена ламана на графіку. Він гарантовано одержує виграш на цій ламаній і, очевидно, вибирає на ній найвищу точку. Координати цієї точки (p^*,v) задають ціну гри v і оптимальну мішану стратегію гравця А:

.

Для гравця В за теоремою 2 маємо:

.

Так само в системі координат (q,v) побудуємо прямі

v = a₁₁ q + a₁₂ (1– q)

v = a₂₁ q + a₂₂ (1– q)

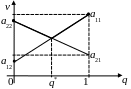
Гравець В розраховує на max(F(A₁,S_B), F(A₂,S_B)) – жирно виділена ламана на графіку. Він гарантовано одержує програш на цій ламаній і, очевидно, вибирає на ній найнижчу точку. Координати цієї точки (q^*,v) задають ціну гри v і оптимальну мішану стратегію гравця B:

.

Приклад. Розв’язати геометрично гру з платіжною матрицею

,

.

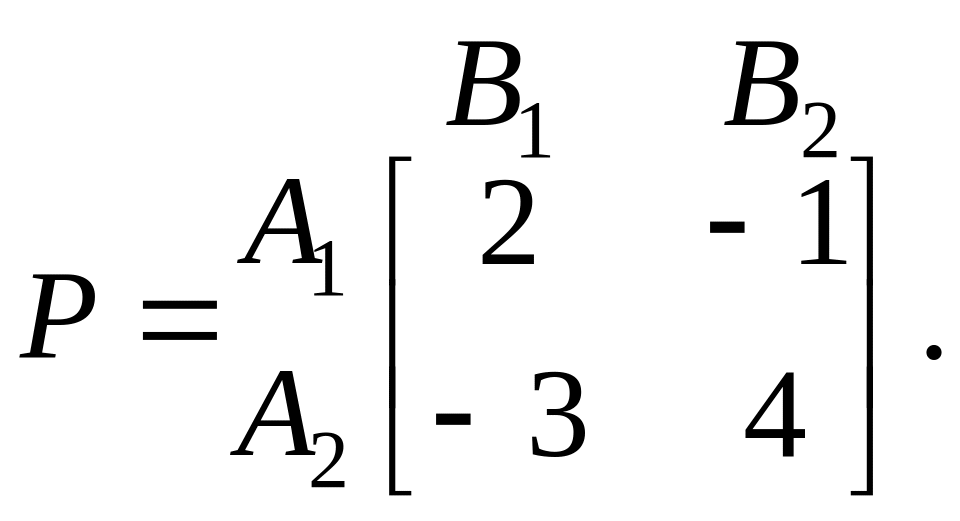
Будуємо відповідні прямі

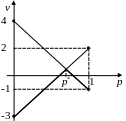
Знайдемо координати точки перетину прямих

2p–3(1–p) = –p+4(1–p),

10p = 7, p^*=0,7,

v = 2·0,7–3·0,3=0,5.

– оптимальна мішана стратегія гравця А.

Для гравця В

,

3q=1,5, q^*=0,5.

– оптимальна мішана стратегія гравця B.

Ціна гри v=0,5.

5.5 Розв’язання ігор та

Такі ігри мають наступні платіжні матриці:

.

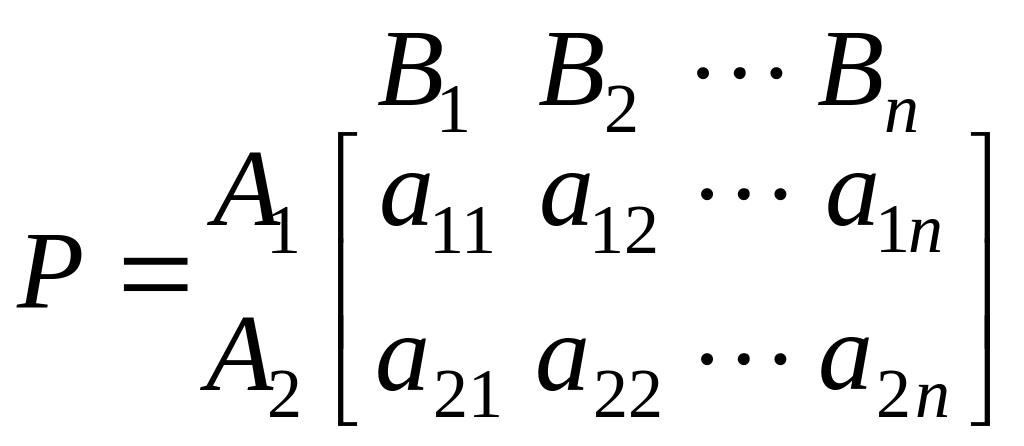
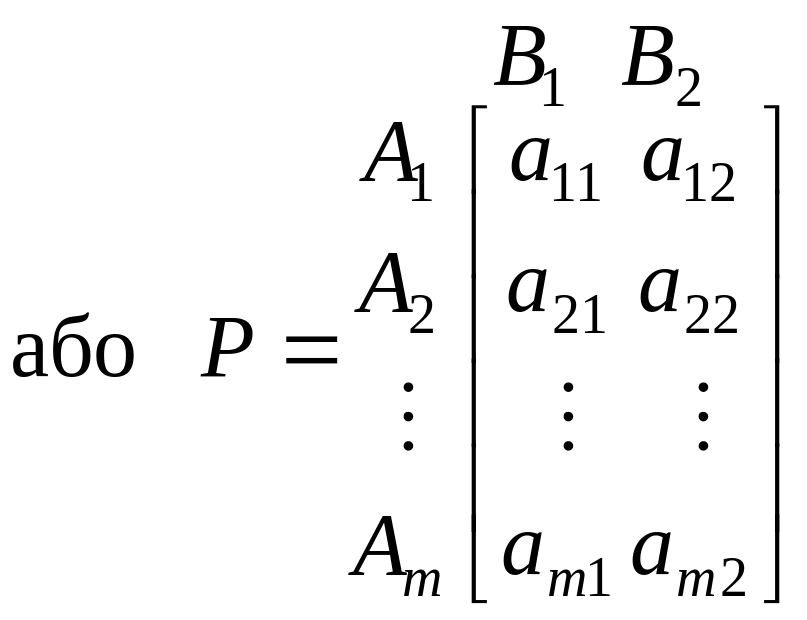Ці ігри краще за все розв’язувати геометрично.

Для визначеності розглянемо гру і застосуємо теорему 2, враховуючи, що мішана стратегія гравця А має вигляд

.

Тоді

,

,

… ,

.

Далі будуємо графіки всіх прямих і обираємо нижню ламану, тобто ламану min(F(S_A,B₁), F(S_A,B₁),…, F(S_A,B_n)), а потім найвищу точку цієї ламаної. Її координати (p^*,v) задають ціну гри v і оптимальну мішану стратегію гравця А. Відрізки цієї ламаної відокремлюють також і активні стратегії гравця В. Решта стратегій не грають ніякої ролі. На активних стратегіях гравця В шукаємо, знаючи ціну гри v, оптимальну мішану стратегію .

Аналогічно розв’язується і гра , але в ній обирають верхню ламану max(F(A₁,S_B), F(A₂,S_B),…, F(A_m,S_B)), а в ній найнижчу точку та її координати.

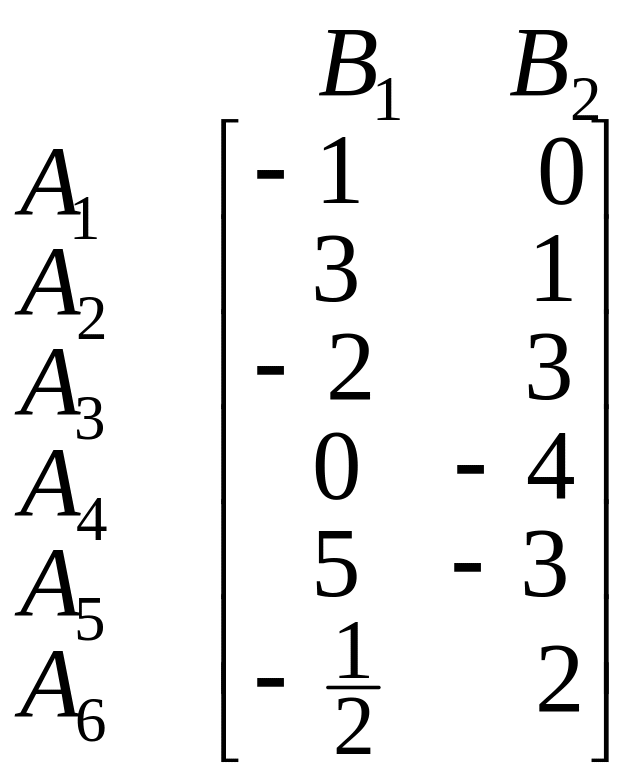
Приклад. Розв’язати гру з платіжною матрицею

.

Розв’язання. Перш за все зауважимо, що стратегія А₂ є більш вдалою, ніж А₁ і А₄. Тобто зрозуміло, що А₁ і А₄ – неактивні стратегії, і платіжна матриця стає такою:

, .

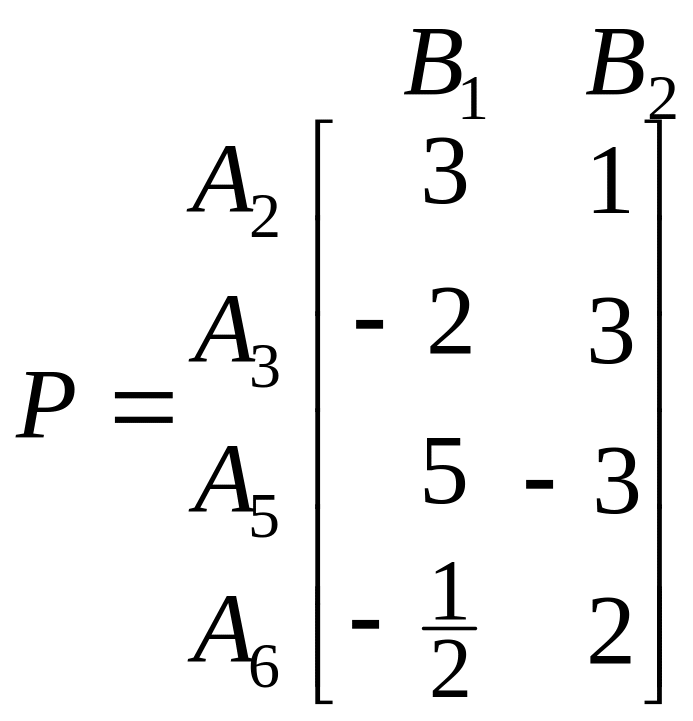Застосуємо теорему 2.

,

,

,

.

Будуємо відповідні прямі

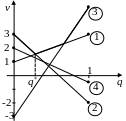
Нижня точка виділеної ламаної знаходиться на перетині ліній і , тобто стратегії А₂ і А₃ є активними. Розв’яжемо систему відповідних рівнянь

2q+15q+3, 7q2,

.

Таким чином, оптимальна мішана стратегія гравця В має вигляд

.

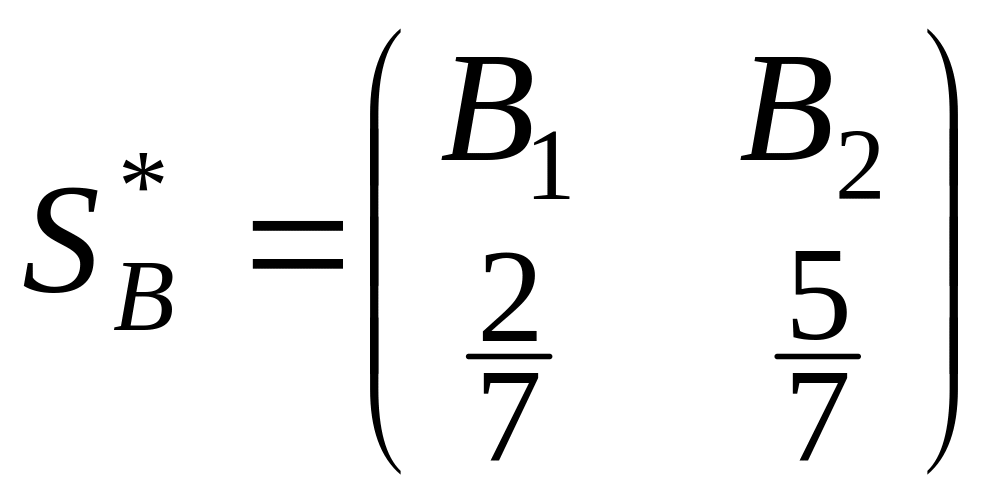Далі знайдемо оптимальну мішану стратегію гравця А. Ми вже знаємо, активними стратегіями гравця А є А₂ і А₂, тобто

.

Тоді

, , .

Таким чином, оптимальна мішана стратегія гравця А

.

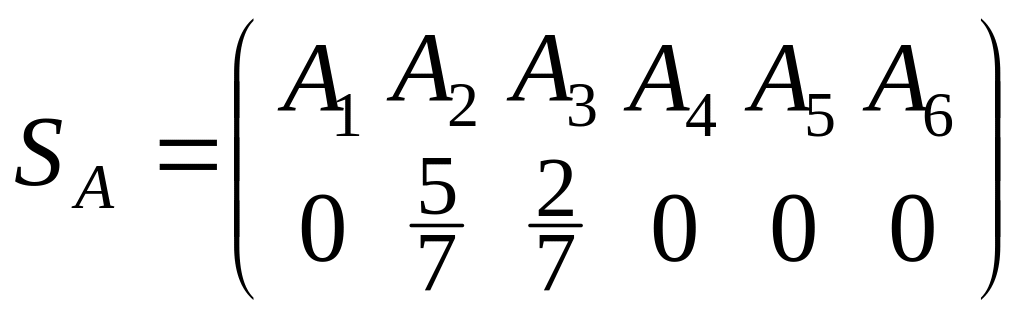Ціна гри .

5.6 Розв’язання ігор

Ігри можуть бути розв’язані трьома методами:

1. розв’язанням відповідних систем лінійних рівнянь;

2. методами лінійного програмування;

3. наближеними методами.

Розглянемо кожен з методів окремо.

І Метод розв’язання системи лінійних рівнянь.

Розглянемо приклад – гру «монетка під пару». Правила гри. Кожний з двох гравців має монети 5, 10, 25 коп. За командою обидва гравці показують свої монети. Якщо монети однакові, тоді вони переходять гравцю А, якщо різні – гравцю В. Розв’язати гру.

Розв’язання. Складемо матрицю платежів цієї гри. Кожен гравець має три стратегії: А₁ – 5 к., А₂ – 10 к., А₃ – 25 к., теж саме для гравця В. Тоді

.

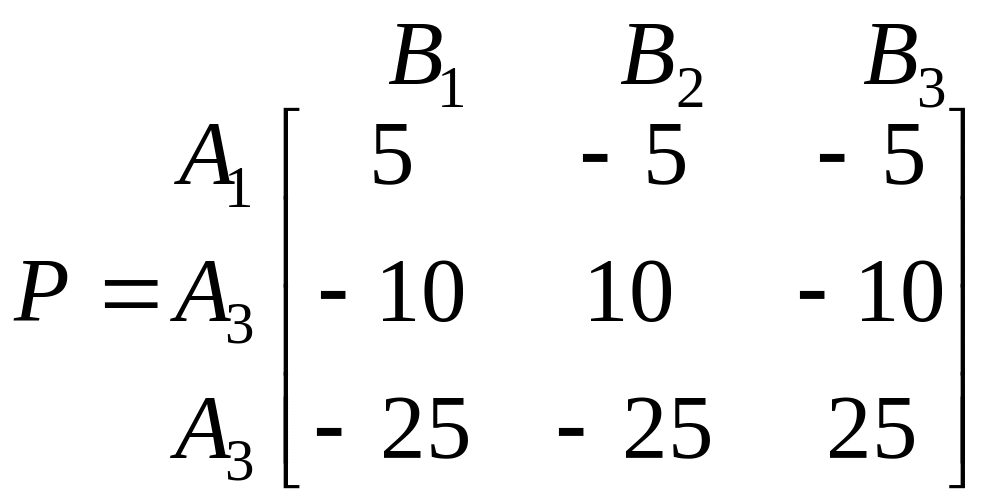Мішана стратегія гравця А

.

Складаємо систему рівнянь

.

Розв’язуючи цю систему рівнянь, одержимо

,

.

Таким чином, оптимальна стратегія гравця А така:

.

Перейдемо до гравця В.

.

Складаємо систему рівнянь

.

Розв’язуючи цю систему рівнянь, одержимо

і , ціна гри .

ІІ Зведення матричної гри до задачі лінійного програмування.

Якщо в матриці платежів є від’ємні елементи, то потрібно додати до кожного елемента матриці таке число, щоб всі елементи стали додатними. Розв’язувати гру методом лінійного програмування потрібно за новою матрицею, а потім від ціни гри відняти те число, яке додавали до елементів матриці.

Гравець А застосовує стратегію , а гравець В відповідає стратегією В_j.

Тут v0 – ціна гри за новою матрицею.

Розділимо обидві частини нерівностей на v і введемо позначки

,

де x_i ≥ 0, i0,1,…,m.

Гравець А намагається збільшити ціну гри v. Тоді одержуємо таку задачу лінійного програмування:

Аналогічними діями одержимо задачу лінійного програмування для гравця В, враховуючи те, що гравець В бажає зменшити ціну гри v.

де .

ІІІ Наближений метод розв’язання ігор .

Розглянемо наближений метод, що має назву метод Брауна–Дж.Робінсон. Він складається з наступного. Проводиться багато партій гри, причому на кож­ному n–му кроці сторона В вибирає таку свою чисту стратегію, яка найкращим чином протидіє накопиченому виграшу сторони А при перших (n–1) ходах. Аналогічним чином діє і сторона А при виборі своєї стратегії.

Приклад. Розв’яжемо гру з платіжною матрицею

.

Літерою «с» позначимо виграш. Якщо зустрінуться однакові числа «с», то будемо вибирати стратегію з меншим номером (за нижчеподаною таблицею).

N партії к	Вибір Аі	Сумарний виграш гравця А при стратегіях Вj				Вибір Bj	Сумарний виграш гравця B при стратегіях Ai
		B1	B2	B3			A1	A2	A3
1	A3	1	7	3	1	B1		4	1	8	4,5
2	A1	1+8	7+2	3+4		B3		4+6	1+3
3	A1	9+8	9+2	7+4		B2	12+2		4+7
4	A2	21	16	17	4	B2	16		18	5	4,5
5	A2	25	21	23	4,2	B2	18		25	5	4,6
6	A2	29	26	29		B2	20	30
7	A3	30	33	32		B1	28		33
8	A2	34	38	38		B1	36		34		4,5
9	A2	38	43	44		B1		42	35
10	A1	46	45	48	4,5	B2	46		42	4,7	4,6

Зроблено 10 кроків задачі. Послідовність чисел в останньому стовпці збігається до ціни гри.

За 10 кроків стратегія А₁ зустрілась 3 рази, А₂ – 5 разів, А₃ – 2 рази, В₁ – 4 рази, В₂ – 5 разів, В₃ – 1 раз. Тоді емпіричні оптимальні мішані стратегії на 10 кроках такі:

, .

Якщо кількість партій прямує до нескінченності, то емпіричні стратегії прямують до оптимальних стратегій.

Питання для самоперевірки

1. Що таке матрична гра?

2. Шо таке платіжна матриця?

3. Що таке нижня та верхня ціна гри, зв'язок між ними?

4. Що таке функція виграшу?

5. Що називається ціною гри?

6. Наведіть основну теорему теорії гри.

7. Що таке мішана стратегія?

8. Що таке чиста стратегія?

9. Що таке активна стратегія?

10. Сформулюйте основну теорему теорії гри.

11. Як розв’язується гра 2x2?

12. Дати геометричну інтерпретацію гри 2x2.

13. Як застосовується геометрична інтерпретація для розв’язання ігор 2xn і mx2?

14. Які існують методи розв’язання ігор mxn?

Задачі для самостійної роботи

1. Побудувати платіжну матрицю для гри за наступним правилом.

Кожний з двох гравців має 3 монети номіналом 5; 10; 25 копійок. Обидва гравця одночасно показують по одній монеті. Якщо монети однакові, то вони переходять до першого гравця, якщо різні − до другого.

2. Гра полковника Блотто.

Полковник має 5 полків і захищає дві рівноцінні позиції. Його противник має 4 полки і атакує ці позиції. Кожний з противників може виділити цілу кількість полків. Полковник виграє 1 грошову одиницю, якщо на кожній з позицій зосередить не менше полків, ніж його противник. У всіх інших випадках він програє 1 грош. одиницю. Скласти матрицю гри.

3. Розв’язати гру при заданій платіжній матриці.

Варіант 1 Варіант 2

. .

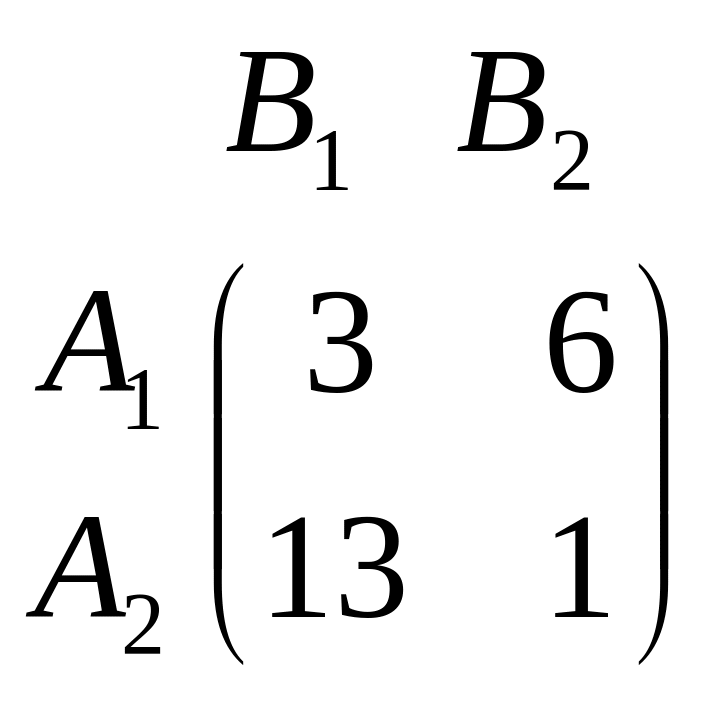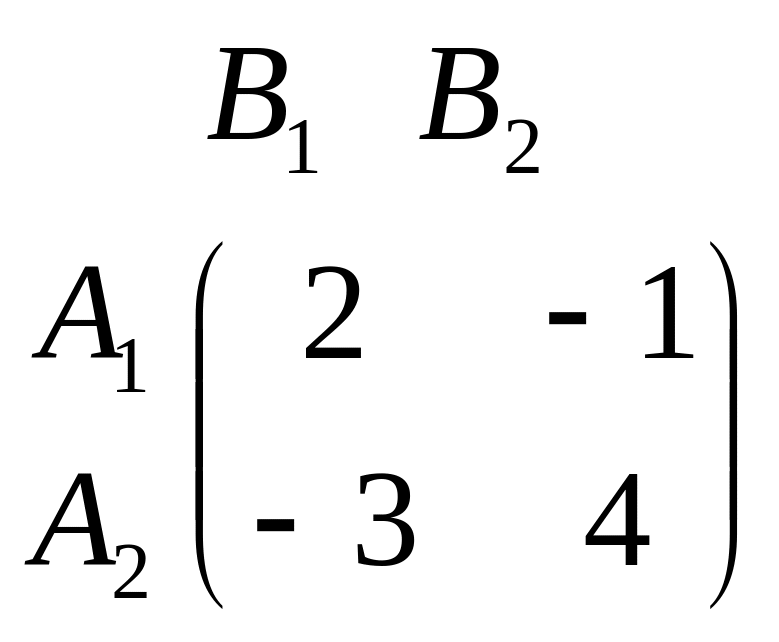Варіант 3

.

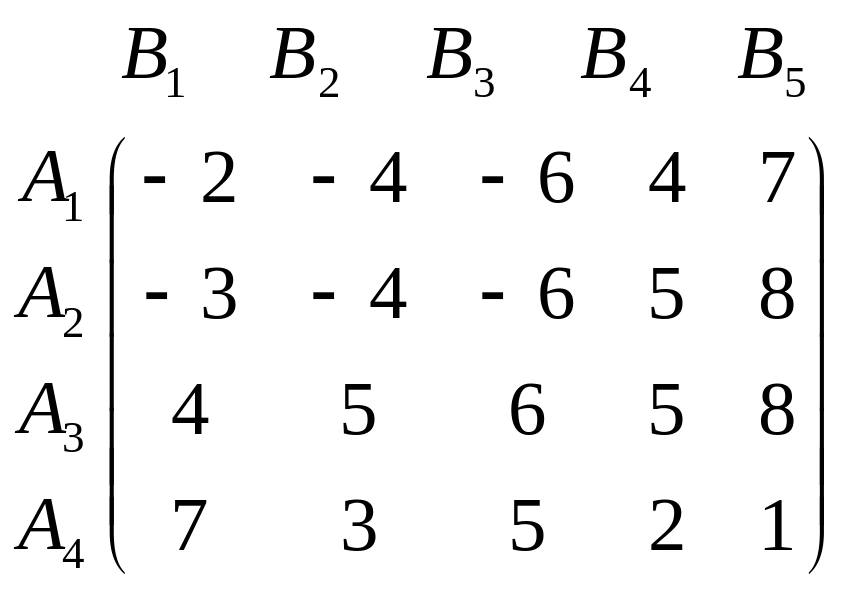4. Розв’язати гру при заданій платіжній матриці за допомогою системи лінійних рівнянь.

Варіант 1 Варіант 2

. .

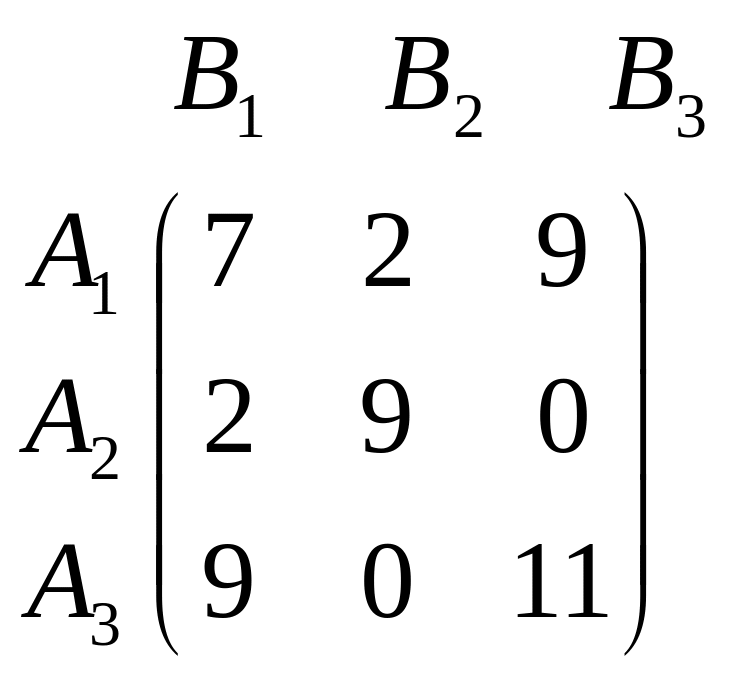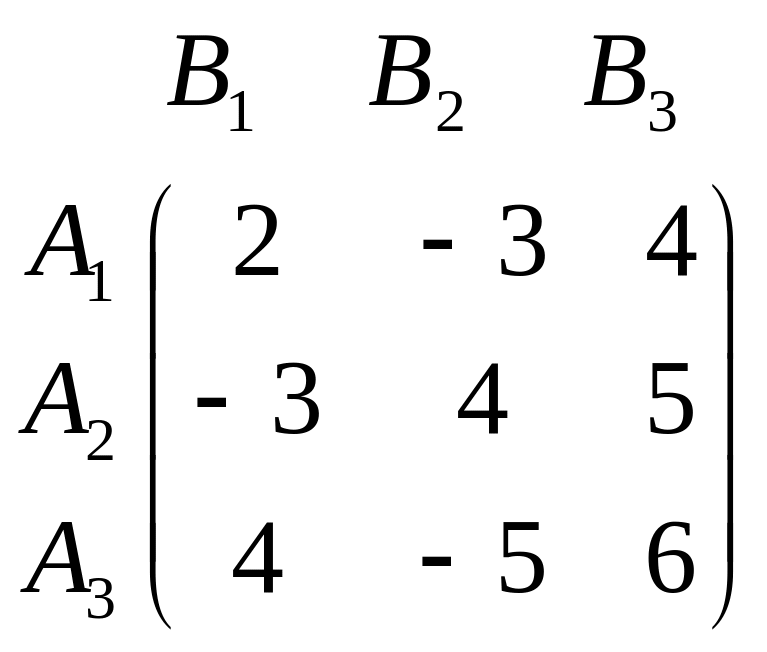5. Розв’язати гру при заданій платіжній матриці методом лінійного програмування.

.

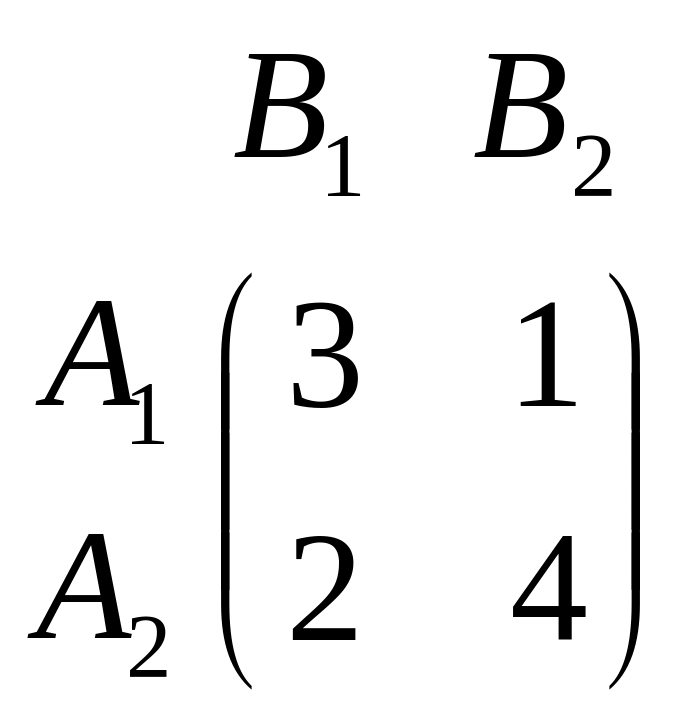6. Розв’язати гру при заданій платіжній матриці геометрично.

.