2.2. Графические области

Графические области делятся на три основных типа – двухмерные графики, трехмерные графики и импортированные графические образы. Двухмерные и трехмерные графики строятся на основании значений, рассчитываемых MathCAD. Обычно по графикам функций проводится исследование функции, т.е. анализ ее поведения.

Построение двухмерного графика функции

Для построения двухмерного графика функции следует нажать кнопку X-Y Plot (Двухмерный график), в шаблоне графика ввести на оси абсцисс имя аргумента, на оси ординат — имя функции.

Если диапазон значений аргумента не задан, по умолчанию график строится в диапазоне значений аргумента от -10 до 10.

Чтобы в одном шаблоне разместить несколько графиков, следует, набрав на оси ординат имя первой функции, нажать клавишу «,» (запятая) и вписать имя второй функции и т. д.

Если две функции имеют разные аргументы, например f1(x) и f2(t), то на оси ординат надо ввести (через запятую) имена обеих функций, а на оси абсцисс (также через запятую) — имена обоих аргументов x и t. Тогда первый график будет построен для первой функции по первому аргументу, второй график — для второй функции по второму аргументу.

Если функций введено несколько, а аргументов два, то график первой функции строится по первому аргументу, графики остальных функций— по второму аргументу.

Если ввести на осях ординат и абсцисс имена двух функций одного аргумента, то будет построен параметрический график функции.

Пример. Построить графики функций в пределах изменения x от 0 до 3.

y1(x):= sin(x) y2(x):=cos(x)

шаг 1 Ввести функции и аргумент шаг 2 Задать вручную

в соответствующих метках графика границы пределов изменения

аргумента

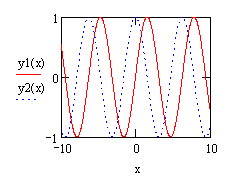
шаг 3 Проверить вид шаг 4 Отформатировать график

графиков функций (толщина 3, тип – линия, задать

сетку по осям X и Yиз 5 линий)

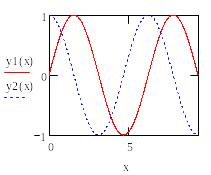
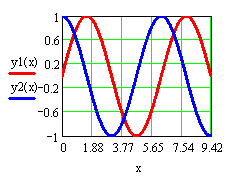
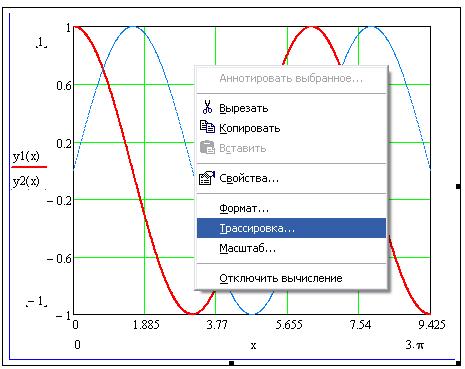
Зачастую требуется исследовать отдельные части графиков - определить интервалы вогнутости - выпуклости, возрастания - убывания, точки минимума - максимума. Иногда необходимо найти корни уравнений или решить систему уравнений, т.е. найти точки пересечения графиков. Эти задачи можно решить приближенно, т.е. графически. Для этого на графике определяются координаты таких точек – указанием их с помощью трассировки.

Алгоритм нахождения точек пересечения графиков Y( ) и P( ):

• Выделить график и выбрать команду контекстного меню Масштабирование (появится диалоговое окно "X-Y Zoom") для увеличения части графика в области точки пересечения.

• На чертеже выделить пунктирным прямоугольником окрестность точки пересечения графиков Y() и P(), которую нужно увеличить.

• Кнопка Масштаб перерисует график.

• Чтобы сделать это изображение постоянным, выбрать Принять.

• Выбрать Трассировка (контекстное меню).

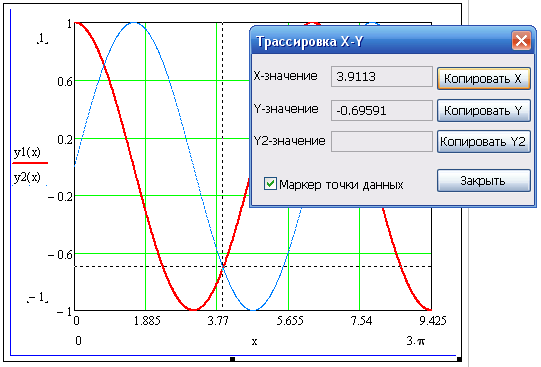
• Внутри чертежа нажать кнопку мыши и переместить указатель мыши на точку, чьи координаты нужно увидеть.

• Выбрать Copy X (или Copy Y), на свободном поле документа набрать Xper := (или Yper :=) и выбрать пункт меню Вставить.

Вычислить значения функций Y( ) и P( ) при полученном значении .

Ответ: