Лабораторная работа № 5 «Символьные вычисления»

1. Вычислить произведение нечётных чисел от –11 до –1. Использовать команды панели Исчисление (Calculus).

Применить знак . Следует задать i, y_i , затем =

2. Вычислить сумму чисел от 5 до 95, исключая числа 10, 20, .. , 90.

Применить знак . Следует задать i, y_i , j, y2_j, затем =

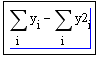3. Вычислить производную функции y = 0,946x³ – 0,663x² + 0,389х в точке x=0,348. Следует задать функцию f(x), затем задать численное значение x и набрать

4. Вычислить 120 значений второй производной от функций: y = 1,264х⁵ – 3,367x³ + 5,638

на интервале от –30 до 30. Задать функцию F(x), значение n, шаг h, дискретную переменную i и вектор Xi. Набрать =.

Аналогичные задачи:

5. Вычислить интегралы функций: , , на интервале от –π.. π.

6. Вычислить значения интеграла функции на интервалах: 0..π/2, 0..π, 0..3π/2, 0..2π.

7. Разложение функции по формуле Тейлора используется для упрощения подынтегральной функции, если интеграл от функции не берется.

Разложить функцию cos(x) по формуле Тейлора (шестого порядка) в окрестности точки

 /2 с помощью панели Symbolic:

Для этого нужно: выбрать в панели ключевое слово series , вести с клавиатуры перед словом series выражение для функции, после него - <имя переменной> = (логическое равенство) , значение точки, в окрестности которой строится разложение> и степень старшего члена в разложении; щелкнуть в рабочем документе вне выделяющей рамки; в рабочем документе отображается только сам многочлен Тейлора (частичная сумма ряда Тейлора).

2 способ. Ввести функцию, выделить переменную, щелкнуть по строке Expand to Series в пункте Variable меню Symbolics (Символика – Переменная – Расширить до ряда ); ввести в окне диалога степень старшего члена в разложении и щелкнуть по кнопке Ok ; в рабочем документе отображается соответствующее разложение с остаточным членом.

Контрольная работа

1. Создать функцию, описывающую положение вершины резца, в зависимости от заданного значения координаты Х. Траектория обработки детали показана на рисунке ниже. Исходные данные (координаты начальной точки x1, y1, радиус R, длину отрезка L, угол наклона fi:=/4) задать самостоятельно. Построить график составленной функции. Найти минимум (максимум) c помощью функции MINERR

Подсказка: задать координаты x1, x2,x3,x4 через параметры из данных (не числами), затем составить функции для каждого участка.

X1:=xc x2:=xc+R … X1:=xc - R x2:=xc ….

Для участка окружности следует использовать задание окружности в декартовой системе координат вывести в виде y(x), для наклонной прямой – уравнение прямой, проходящей через две точки, тоже вывести в виде y(x).

Построить графики составленных функций в одной координатной системе, проверить правильность задания функций ( по виду полученных графиков). Составить единую функцию, используя несколько вложений if: y(x):=if(x<x1,0,if(x<=x2,y1(x), …). Построить график функции.

Задать начальное приближение для абсциссы точки экстремума. Используя вычислительный блок, найти координаты экстремума функции на выбранном участке.

Выбрать один из вариантов схемы для решения.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

00

2. Построить графики, задав фигуры векторами. Найти приближенно точки пересечения двух фигур. Задать функции, описывающие фигуры. Определить численно координаты точек пересечения, если дано (выбрать для своего варианта):

№ варианта	a	b	R	r	c	d		dx	dy
1	20	40		10				20	30
2				15		40	60	30	5
3			75	25				60	20
4	25	38				38	45	30	20
5	25	50		15				33	-17
6	15	25				40	60	23	-17
7	15	25				40	60	10	39
8						40;20	60	5	35
9	25;10	38;20						20	40
10	25;10	38;20						10	32
11			40		55			45	40
12			40		60			20	10
13	25	38			40			30	-10
14			30			40	45	32	32
15	25	38		18				27	15

Обозначения: а – малая полуось эллипса;

b – большая полуось эллипса;

R – радиус большой окружности;

r – радиус малой окружности;

c –сторона квадрата;

d –сторона ромба;

 - угол при острой вершине ромба.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15