1.6. Закон больших чисел (law of large numbers)
1.6.1.Закон больших чисел в форме Чебышёва(1846,1867)
Неравенство
Чебышёва.
Для любой случайной величины
,
у которой
,
имеем
,
.
(1.6.1)
Доказательство.
Поскольку
,
где
– функция распределения случайной
величины
,
и в области её интегрирования
,
то
.
Усилим
это неравенство, распространяя
интегрирование на все значения
,
и получим:
.
Теорема Чебышева(1867).
Если
-
независимые случайные величины и
то
,
.
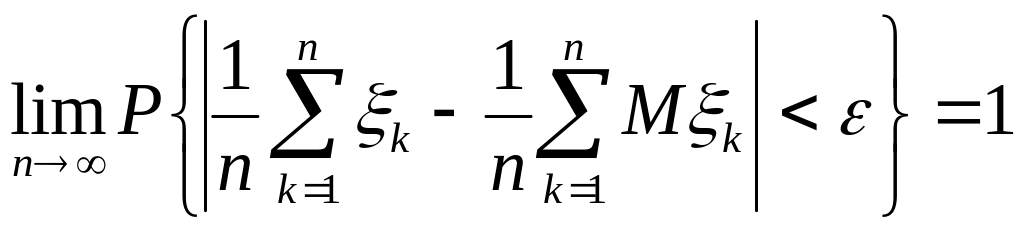(1.6.2)
Доказательство.
Т.к.
,
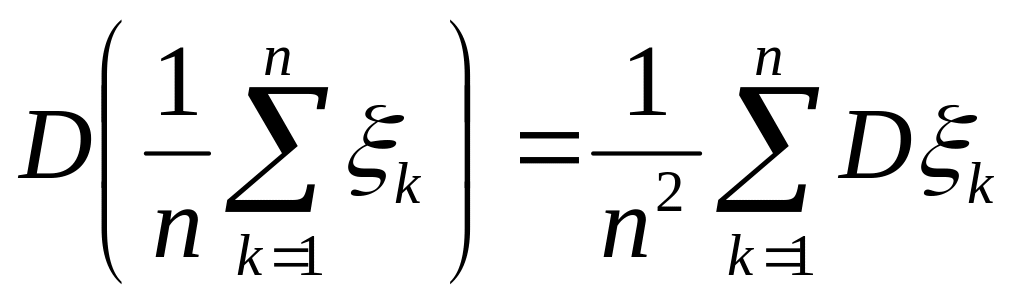а значит
,
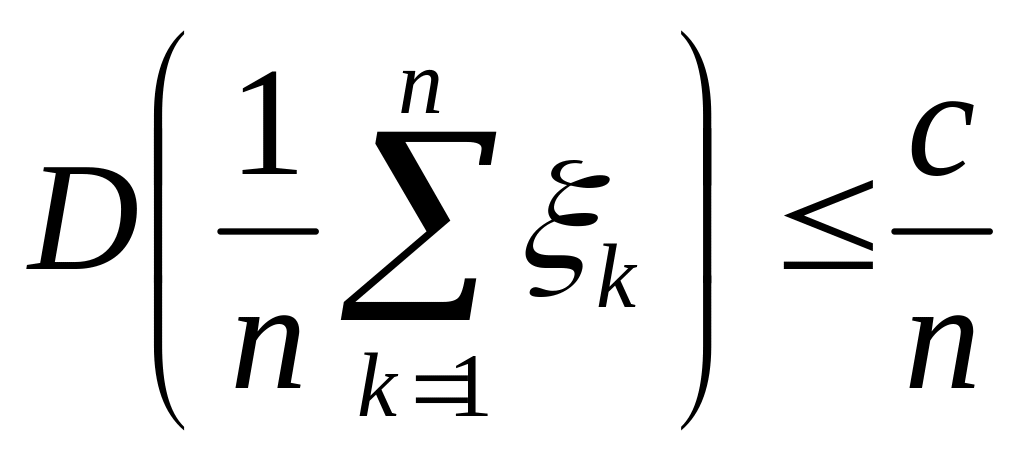то, используя (1.6.1), имеем
.
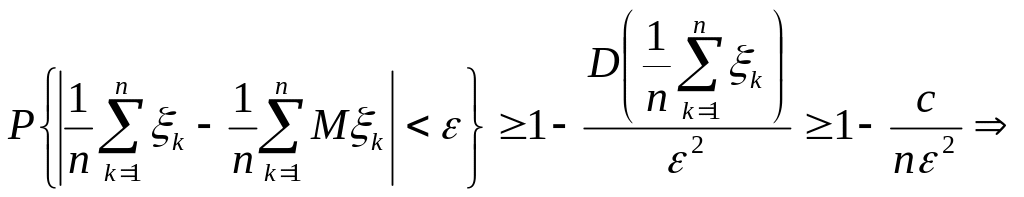
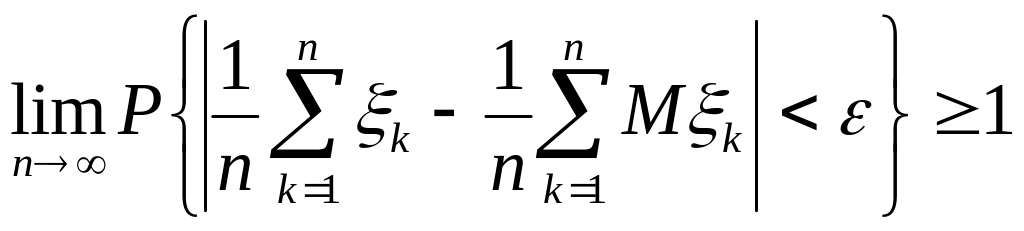Поскольку
вероятность не может быть больше 1, то
теорема доказана.
1.6.2.Следствия теоремы Чебышева
Теорема
Бернулли(1713).
Если в
независимых испытаниях число появлений
события
равно
,
а вероятность наступления события
в каждом из
испытаний
равна
,
то
,
.
(1.6.3)
Доказательство.
Пусть
равно числу наступлений события
при k
испытаниях, тогда
.
Т.к.
,
то
теорема
Бернулли есть
частный случай теоремы Чебышева.
Теорема Пуассона(1837). Если в независимых испытаниях число появлений события
равно
,
а вероятность наступления события
в испытании
равна
,
то
,
.
(1.6.4)
Доказательство аналогично приведенному в теореме Бернулли.
Теорема Хинчина(1929). Если независимые случайные величины имеют
одинаковое
распределение и
,
то
,
.
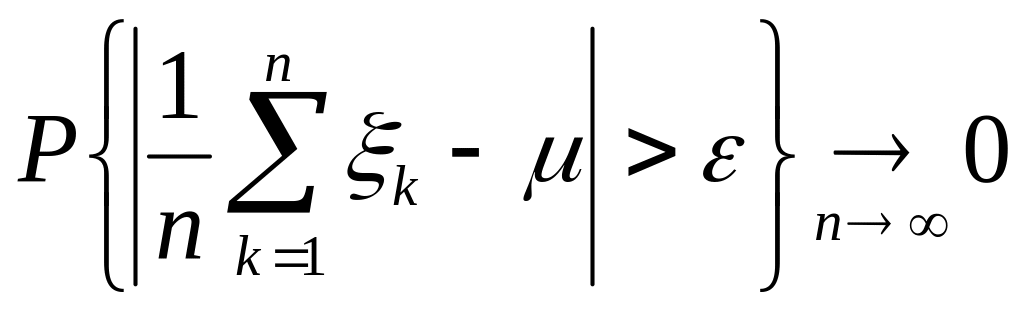(1.6.5)
Теорема Маркова(1907). Если для независимых случайных величин ,
,
(1.6.6)
то
,
.
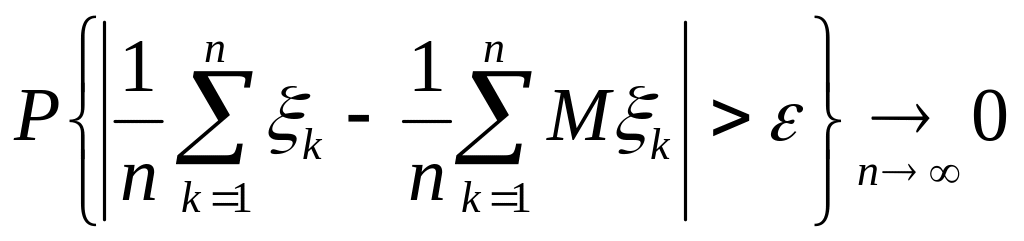(1.6.7)
1.6.3.Усиленный закон больших чисел (strong law of large numbers)
Теорема Бореля(1909). Если в независимых испытаниях, - число появлений события , а
- вероятность наступления события в каждом из испытаний, то
.
(1.6.8)
Этот
результат имеет простую трактовку: для
достаточно большого числа испытаний
вероятная частота
события приближённо равна его вероятности
.
Теорема
Колмогорова(1930).
Последовательность взаимно независимых
случайных величин
подчиняется УЗБЧ, если она удовлетворяет условию
.
(1.6.9)
Следствие
теоремы Колмогорова.
Если
,
то последовательность
взаимно независимых случайных величин подчиняется УЗБЧ.
1.7.Метод характеристических функций (method characteristic functions)
Представляет собой применение преобразования Фурье к комплексным случайным величинам:
,
(1.7.1)
где
и
– действительные случайные величины,
.
На комплексные случайные величины распространяется понятие математического ожидания:
,
(1.7.2)
при условии использования в различных оценках их абсолютных значений.
1.7.1.Характеристические функции
Определение. Характеристической
функцией
действительной случайной величины
называется математическое ожидание
случайной величины
:
(1.7.3)
Для
дискретной случайной величины
,
распределение вероятностей которой
сосредоточено в целых точках
,
т.е.
,
причем
,
(1.7.4)
характеристическая функция представляется разложением в ряд Фурье
,
(1.7.5)
имеет
период
и коэффициенты
,
(1.7.6)
Для непрерывной случайной величины с плотностью p(x), характеристическая функция
(1.7.7)
является
интегралом Фурье от функции
.
Для
интегрируемой функции
,
т.е. для которой
,
(1.7.8)
плотность
вероятности
определяется через обратное преобразование
Фурье:
,
.
(1.7.9)
Пример. Случайная величина равномерно распределена в интервале (-a, a).
Характеристическая функция равна
.
(1.7.10)
Теорема.
Для характеристических
функций
и
случайных величин
и
,
что
,
где
,
(1.7.11a)
верно
.
(1.7.11b)
Доказательство:
.