§6. Сумма и произведение нескольких натуральных чисел

Определение. Пусть nN, тогда сумма n натуральных чисел а₁, а₂, … , а_n обозначается и определяется индуктивно следующим образом:

1. 

2. Если сумма определена для к натуральных чисел (k<n) то

Замечание. Если все слагаемые в определении равно а, то получим определение n-кратного числу а

na=

n раз

Определение. Пусть nN, тогда произведение n натуральных чисел а₁, а₂, … , а_n обозначается и определяется индуктивно следующим образом:

1. 

2. Если произведение определено для к натуральных чисел (k<n) то

Замечание. Сумма и произведение нескольких натуральных чисел не зависит от того, как поставить скобки, а также от того, в каком порядке записать слагаемые (сомножители). Следует из свойств коммутативности, ассоциативности.

;

Теорема 1.

1.(

2.(

Доказательство:

1. ММИ(n)

n=2 (a₁+a₂)b=a₁b+a₂b

n=k (

n=k+1 ( +

2. ММИ (m)

m=1

m=k

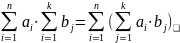
m=k+1

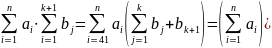
Свойство. a, u N na=na

Доказательство:

ММИ(n)

n=1 1a=a 1a=a1=a

n=k ka=ka

n=k+1 (k+1)a= =ka+a=ka+a=(k+1)a

k раз

Следcтвие. a, b, m, n N

1)(m+n)a=ma+na

2)(mn)a=m(na)

3)manb=(mn)(ab)

4)(m-n)a=ma-na

5)m(a+b)=ma+mb

6)m(a-b)=ma-mb

Доказательство:

1)ma+na=ma+na=(m+n) a=(m+n)a

2-6 самостоятельно.

Свойство. a, b, m, n N

1)a^m+n=a^maⁿ

2)a^mn=(a^m)ⁿ

3)a^m-n=a^maⁿ, если m>n

4)(ab)^m=a^mb^m

5)(ab)^m=a^mb^m , если частное существует.

Доказательство:

1. a^maⁿ=  = =

m раз n раз m+n раз

2-5 самостоятельно.

§7 Конечные и счетные множества

Определение 1: множества X и Y называются равномощными, если между ними взаимно-однозначное соответствие (биекция).

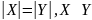
Замечание 1: конечные равномощные мн-ва - это мн-ва с одинаковым кол-вом эл-тов.

Замечание 2:

Примеры счетных мн-в, но мощность мн-ва действ. чисел. R не является счетным мн-вом.

Св-во: отношение «быть равномощными» является быть отношением эквивалентности.

Док-во:

• Симметричность

,биекция биекция

• Транзитивность

биекция

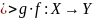биекция

биекция .

Определение 2: пусть n . Отрезком натурального ряда называется множество

Примеры:

Определение 3: мн-во Х равномощное отрезку 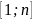называется конечным мн-вом, число n называется количеством элементов конечного множества.

Множество, которое не является конечным, называется бесконечным.

Теорема 1: конечное множество равномощно только одному отрезку натурального ряда

Док-во: отрезок не может быть равномощным отрезку 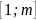, если m n

ММИ(n)

n=1

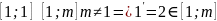
Противоречие

n=k

n=k+1

если m=1, то !?

если m>1

можем считать f(k+1)=l+1

Рассмотрим ограничения отображения 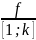, - биекция, то ни один из элементов отрезка не отображается в элемент l+1.

f- инъекция 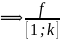– инъекция

– биекция .

Пусть , число n называется количеством элементов множества Х.

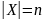
Следствие: два равномощных множества имеют одно и тоже кол-во элементов.

Док-во: пусть

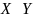
k=n.

Теорема 2: каждое непустое конечное множество содержит наибольший и наименьший элемент.

Док-во: ММИ по количеству элементов n

n=1

n=2 A,B

A>B, A<B,A=B

n=k каждое конечное множество содержит наибольший и наименьший элемент

n=k+1

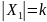
По предположению индукции в множестве выберем наибольший элемент В. Сравниваем А и В и выбираем наибольший элемент. Аналогично находим наименьший элемент множества Х.

Теорема 3: множество всех натуральных чисел бесконечно.

Док-во:

ОП по теореме 2 в каждом конечном множестве существует наибольший элемент А

А+1>A?!