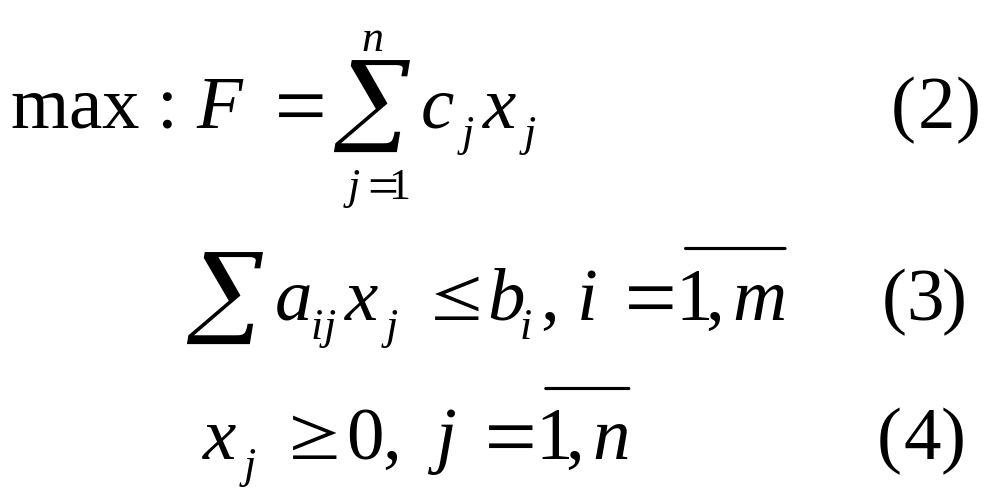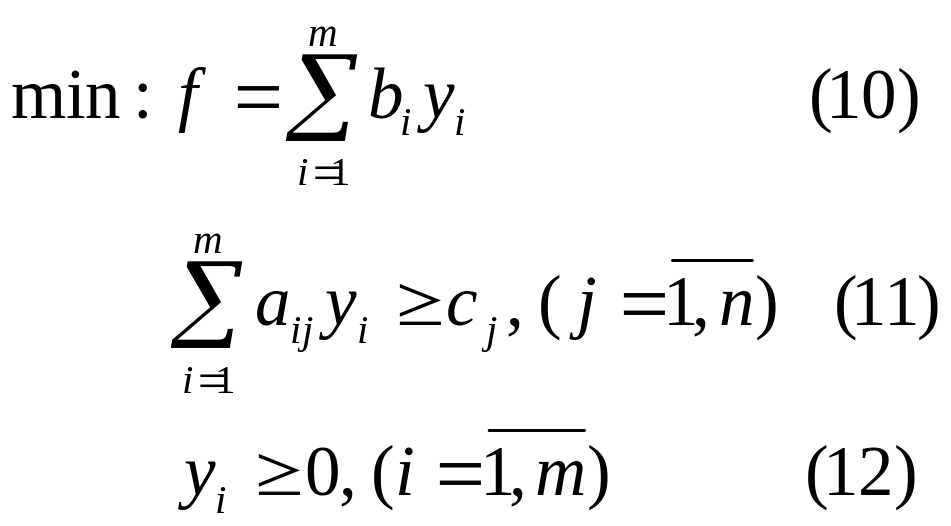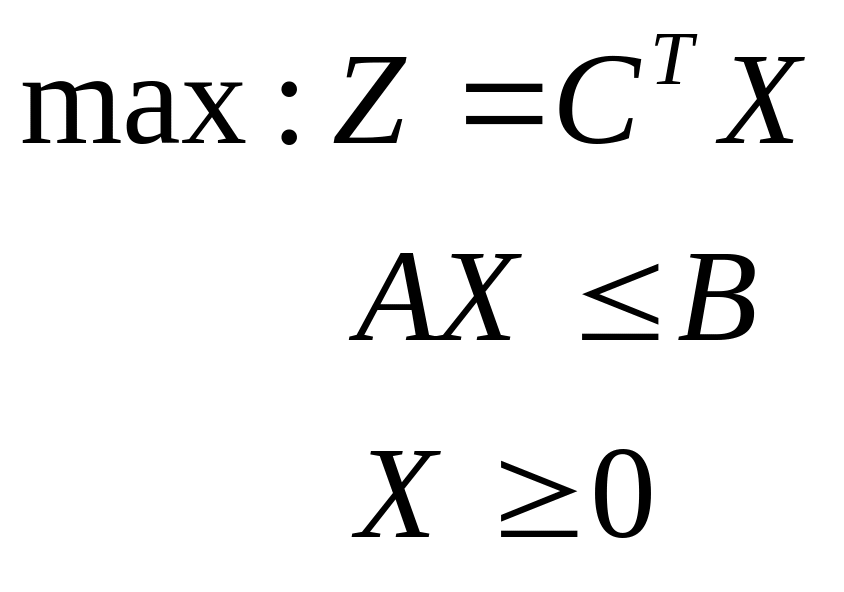2.4 Двоїстість в лінійному програмуванні

2.4.1 Поняття двоїстості. Побудова двоїстих задач та їх властивості.

Двоїстість слугує для ілюстрування одного з законів діалектики ─ закону єдності та боротьби протилежностей. До аналогічних в математиці відносяться поняття , «диференціювання» та «інтегрування», у фізиці ─ «додатній» та «від’ємний» заряди, «північний» та «південний» магнітні полюси та ін.

Поняття двоїстості розглянемо на прикладі задачі оптимального використання сировини.

Постановка задачі. Нехай на підприємстві вирішили раціонально використати відходи основного виробництва. В плановому періоді з’явилися відходи сировини видів з обсягами одиниць ( ). З цих відходів, враховуючи спеціалізацію підприємства, можна налагодити випуск видів неосновної продукції. Позначимо через норму витрат сировини виду на одиницю -ої ( ) продукції, ─ вартість реалізації одиниці -ої продукції (реалізація забезпечена).

Невідомі величини задачі: ─ обсяги випуску -ої продукції, що забезпечують підприємству максимальну виручку.

Математична модель задачі:

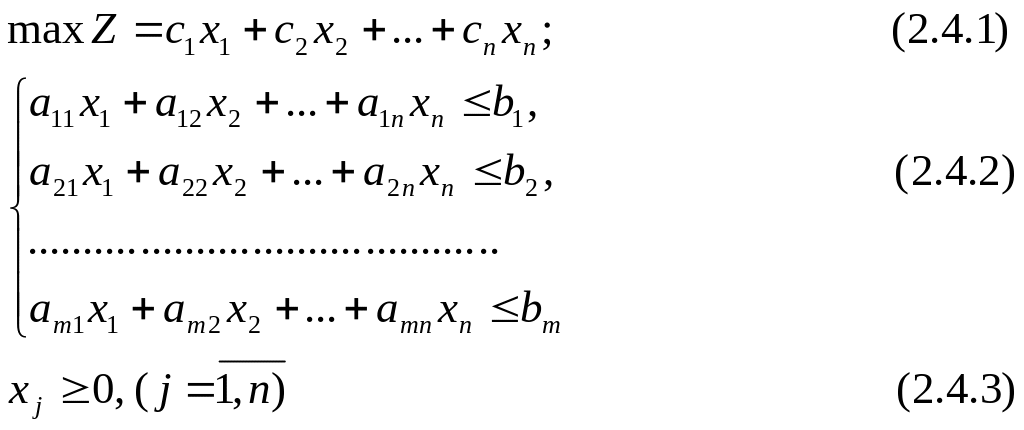
Отже, ми отримали пару задач, які називаються двоїстими:

В матричній формі пара двоїстих задач записується так:

Змінні називаються двоїстими оцінками або (як їх назвав Л.В. Канторович, який відкрив двоїстість) об’єктивно обумовленими оцінками. В зарубіжній літературі їх також називають тіньовими цінами.

Задачі (2)-(4) та (5)-(7) називають парою взаємно двоїстих ЗЛП. Так як задачі (2)-(4) та (5)-(7) записані в симетричній формі, їх прийнято називати парою симетричних двоїстих задач.

Можна показати, що якщо в якості прямої прийняти задачу (5)-(7) про визначення оптимальних оцінок на сировину, то двоїстою до неї буде задача (2)-(4) про визначення оптимального плану випуску продукції.

З моделей (2)-(4) та (5)-(7) безпосередньо видно, що маючи математичну модель однієї з цих задач, можна легко побудувати модель двоїстої до неї задачі.

Співставляючи моделі (2)-(4) та (5)-(7) пари двоїстих задач, можна встановити спеціальні взаємозв’язки:

Перш за все обидві моделі записуються в симетричній формі.

1. Якщо пряма задача на 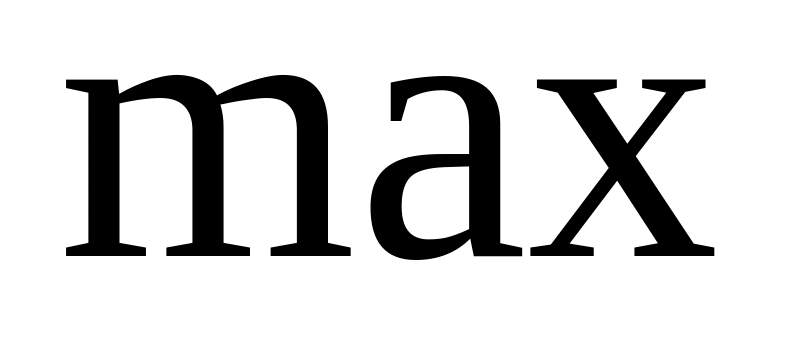, то двоїста ─ на ;

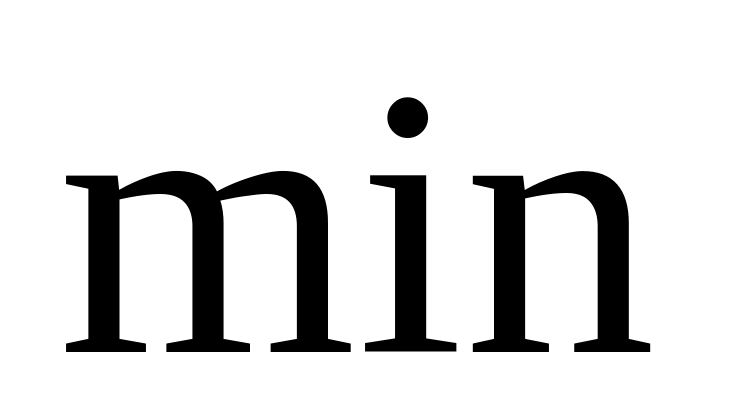2. Коефіцієнти ЦФ прямої задачі 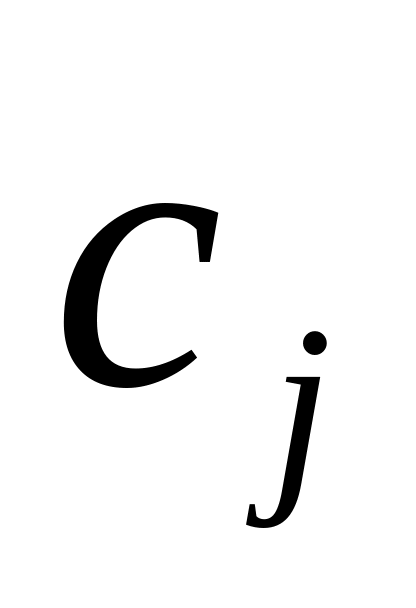стають вільними членами обмежень двоїстої задачі;

3. Вільні члени обмежень прямої задачі стають коефіцієнтами ЦФ двоїстої задачі;

4. Матриця обмежень двоїстої задачі є транспонованою по відношенню до матриці обмежень прямої;

5. Якщо пряма задача розв’язується на , то її система обмежень містить нерівності типу 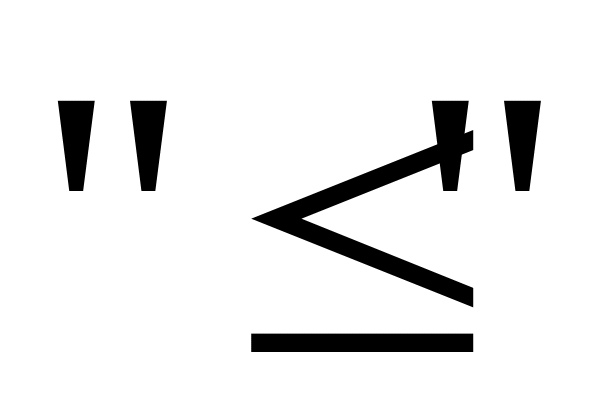, при цьому двоїста задача розв’язується на і її система обмежень має вид нерівностей типу ;

6. Кількість обмежень прямої задачі дорівнює кількості змінних двоїстої, а кількість обмежень двоїстої ─ кількості змінних прямої;

7. Всі змінні в обох задачах невід’ємні.

Пара задач (2)-(4) та (5)-(7) називається симетричною парою двоїстих задач.

Якщо серед обмежень прямої задачі наявні рівності або на деякі змінні не накладена умова невід’ємності, то побудувавши двоїсту їй задачу, отримаємо пару несиметричних двоїстих задач. Кожне обмеження-рівність необхідно лише замінити парою нерівностей протилежного змісту (наприклад, на та ), а змінні , на які не накладена умова невід’ємності ─ різниця та , де , тоді .

Діючи за приведеними вище правилами (1)-(6), отримаємо:

Пряма задача

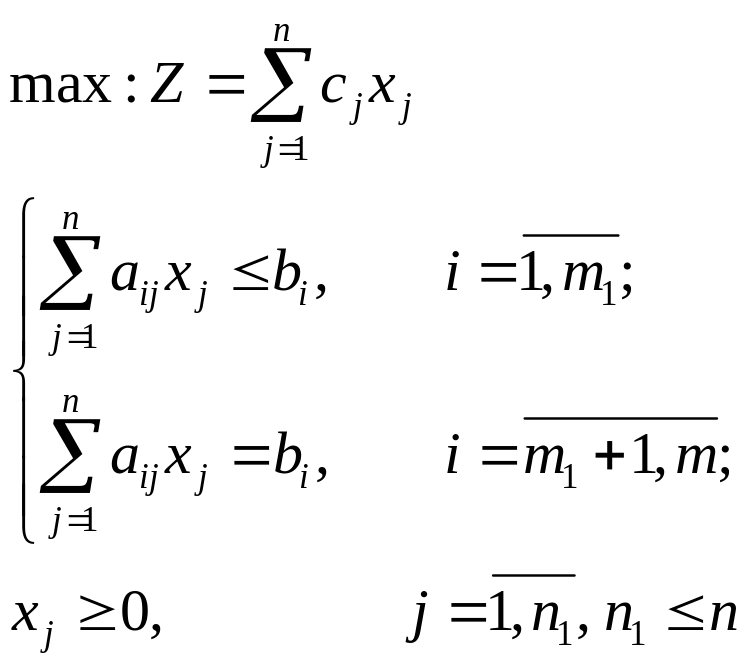
Двоїста задача

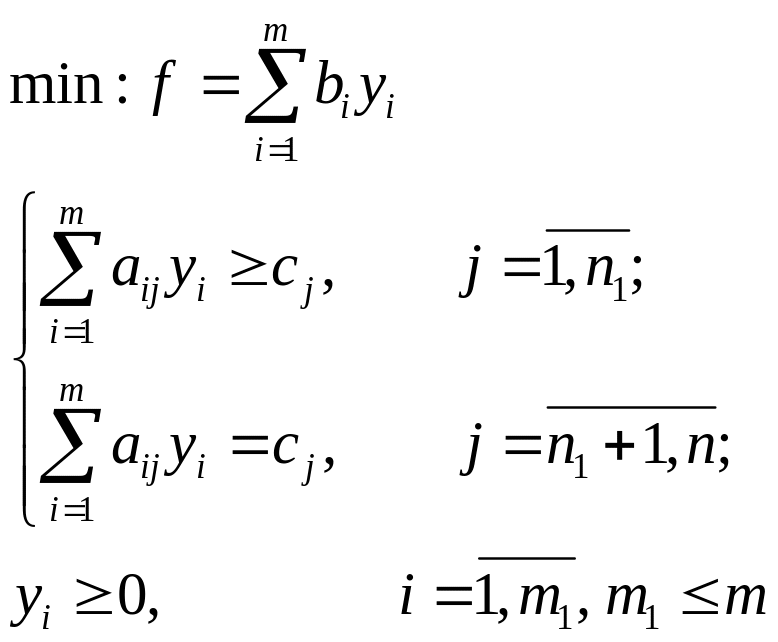
Очевидно, що задача двоїста до двоїстої співпадає з вихідною. Тому немає різниці, яку задачу прийняти в якості прямої, а яку ─ двоїстої.

Двоїста задача зі змішаними умовами складається за наступними правилами:

1. Якщо на змінну прямої задачі накладена умова невід’ємності, то 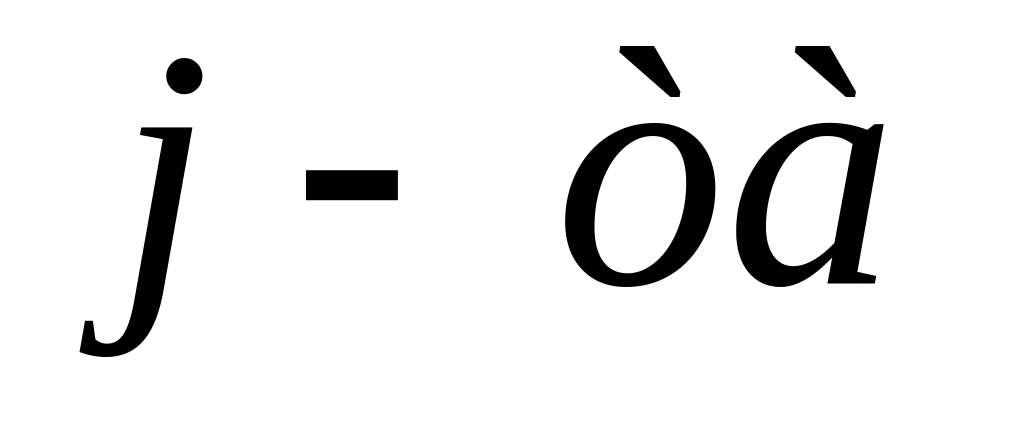умова системи обмежень двоїстої задачі є нерівністю й навпаки;

2. Якщо на змінну прямої задачі не накладена умова невід’ємності, то обмеження двоїстої задачі залишається у виді строгої рівності;

3. Якщо в прямій задачі є обмеження рівності, то на відповідні змінні двоїстої задачі накладається умова невід’ємності.

Пара взаємно двоїстих симетричних задач у вигляді канонічних сум має вид:

Пряма задача

Двоїста задача

або в матричній формі:

Приклад 2.4.1. Виходячи зі спеціалізації та своїх технологічних можливостей підприємство може випускати 4 види продукції. Збут любої кількості забезпечений. Для виготовлення цієї продукції використовуються трудові ресурси, напівфабрикати та станкове обладнання. Загальний обсяг ресурсів (в розрахунку на трудовий тиждень), витрати кожного ресурсу на одиницю продукції, що випускається та прибуток, що отримано за одиницю продукції, наведені в таблиці 2.4.1.

Необхідно скласти математичну модель прямої та двоїстої задачі..

Таблиця 2.4.1

Ресурси		Продукція				Обсяг ресурсів
		П1	П2	П3	П4
Р1	Трудові ресурси, чол-год.	4	2	2	8	4800
Р2	Напівфабрикати, кг.	2	10	6	0	2400
Р3	Станкове обладнання, станко-год.	1	0	2	1	1500
Ціна одиниці продукції, грн.		65	70	60	120

Розв’язок:

Нехай ─ обсяги продукції П1, П2 П3 П4, що плануються до випуску ─ сума очікуваної виручки.

Математична модель прямої задачі:

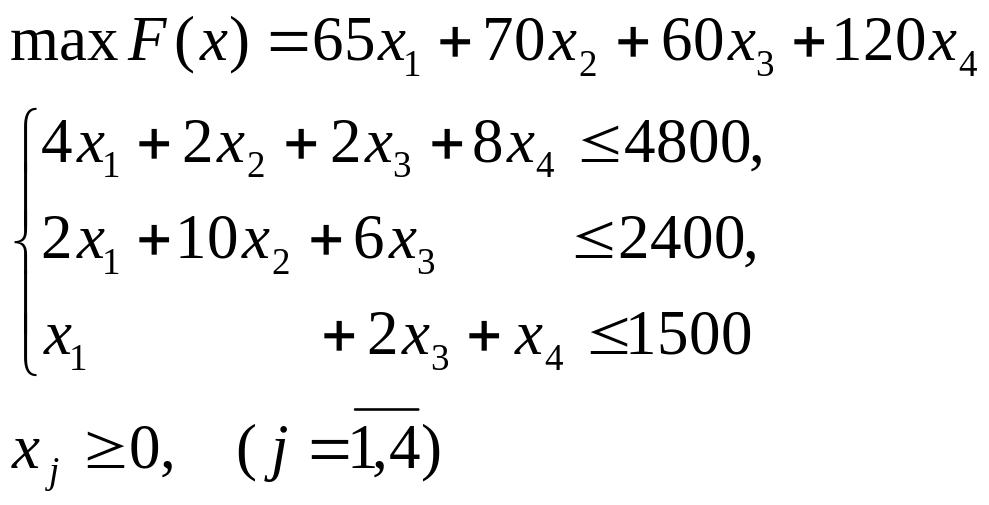
Математична модель двоїстої задачі: