Определенный интеграл.

Указания.

При вычислении определенного интеграла методом замены переменной возможны два пути: либо, найдя первообразную функцию, вернуться к первоначальной переменной и уже потом применить формулу Ньютона-Лейбница, либо, совершая подстановку, соответственно изменить и пределы интегрирования. Тогда отпадает необходимость возвращения к первоначальной переменной. Более целесообразным в большинстве случаев является второй путь.

Примеры вычисления интегралов.

Задача 7.

Вычислить

Решение. Применим подстановку cosx = t, sinx dx = - dt.

Определим новый промежуток интегрирования. Если х = 0 , то

cos0 = 1 и t = 1, если x = π/2, то cosπ/2 = 0 и t = 0, следовательно,

Задача 8. Вычислить

Решение. Применим подстановку

t = t² = e^x – 1, 2tdt = e^xdx, dx= .

Если x = 0, то t = 0, если x =ln2, то t= , следовательно,

Задача 9. Вычислить площадь фигуры, ограниченной следующими параболами y = x² и x = y².

Решение. Обе параболы проходят через начало коорди­нат, первая парабола симметрична оси Oу, вторая - сим­метрична оси Ox.

Найдем точки пересечения данных кривых. Для этого ре­шим систему уравнений:

Следовательно, параболы пересекаются в точках O(0;0) и

B(1;1). Теперь легко определить площадь фигуры ОАВСО, рассматривая ее как разность площадей двух кри­волинейных

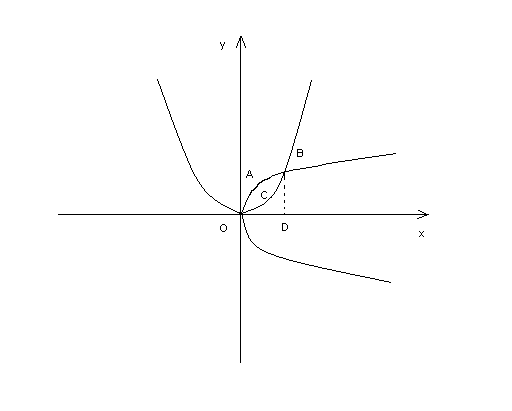
Рис. 4

трапеций ОАВDО и ОСВDО. Воспользовавшись формулой

получим

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Сформулируйте определения первообразной функции. Докажите, что любые две первообразные для одной и той же функции отличаются на постоянное слагаемое.

2. Что называется неопределенным интегралом? Каков его геометрический смысл?

3. Укажите целесообразные подстановки для отыскания интегралов:

∫cosx cosx(sinx)dx,

4. Укажите задачи, приводящие к понятию определенного интеграла.

5. Что называется определенным интегралом от данной функции на данном отрезке?

6. Каков геометрический смысл определенного интеграла от данной функции у = f(x) на отрезке [а, b] в системе декартовых координат?

7. Сформулируйте теорему существования определенного интеграла.

8. Сформулируйте простейшие свойства определенного ин­теграла.

9. Напишите формулу Ньютона-Лейбница.

10. В чем состоит метод замены переменной (метод подста­новки) в определенном интеграле?

11. Какие геометрические задачи решаются при помощи опре­деленного интеграла?

Тема №5 Обыкновенные дифференциальные уравнения 1-го и 2-го порядка.

Э.С. Маркович, ч.1, раздел 6, глава 16, §§ 79,80, упражнения.

Дифференциальным уравнением называется соотношение, связывающие аргумент, неизвестную функцию, ее производные и дифференциалы.

Если функции, входящие в дифференциальные уравнения зависят от одного аргумента, то дифференциальные уравнения называются обыкновенными.

Порядок данного дифференциального уравнения определя­ется порядком наивысшей производной, входящей в уравнение.

Проинтегрировать данное дифференциальное уравнение - значит найти все функции, ему удовлетворяющие, т.е. обращающие его в тождество. Общее решение дифференциального уравнения записывается в виде

F (x, y, C₁, C₂, ... , C_n) = 0.

Если придать произвольным постоянный частные значения, то это даст частные решения дифференциального уравнения.

Дифференциальное уравнение первого порядка записыва­ется в общем виде

f(x, y, y') = 0,

а его общее решение

F(x,y,c) = 0.

С геометрической точки зрения интегрирование диффере­нциального уравнения первого порядка представляет задачу нахождения семейства кривых. Только введение начальных условий позволяет выделять отдельные кривые.

Дифференциальные уравнения с разделенными переменными задаются в виде

M(x)dx + N(y)dy = 0.

Дифференциальные уравнения с разделяющимися переменны­ми

M₁(x)N₁(y)dx + M₂(x)N₂(y)dy = 0

приводятся к дифференциальным уравнениям с разделенными переменными делением всех членов на N₁(y)M₂(x).

Однородное дифференциальное уравнение первого порядка

P(x, y)dx + Q(x, y)dy = 0

где Р(x, y) и Q(x, y) - однородные функции одина­кового измерения, заменой y = x∙ u, где u - новая функция от x, приводится к уравнению с разделяющимися переменными.

Линейное дифференциальное уравнение первого порядка

у' + P(x)y = Q(x)

заменой y = u ∙ v приводится к уравнению с разделяю­щимися переменными.

Для решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами

у''+ py' +qy = 0

необходимо составить соответствующее характеристическое уравнение, т.к. решение дифференциального уравнения зависит от корней характеристического уравнения.

Общее решение линейного неоднородного дифференциаль­ного уравнения

у'' + py' +qy = f(х)

выражается суммой его какого-либо частного решения и об­щего решения соответствующего однородного уравнения.

Правая часть неоднородного дифференциального уравне­ния второго порядка может иметь вид:

f (х) = P_n(x),

или

f (х) = P_n(x)e^kx ,

или

f (х) = e^kx[Q_n(x)cosβx + P_m(x)sinβx]

В учебнике Э.С.Марковича в §§ 79,80 разобраны примеры, а также дано упражнение для самостоятельной работы. Эти. упражнения необходимо обязательно проделать.