
- •Математика
- •Предисловие
- •Программа курса математики Введение
- •Раздел I. Элементы линейной алгебры и аналитической геометрии.
- •Раздел II. Дифференциальное исчисление функции одной переменной.
- •Раздел III. Дифференциальное исчисление функций нескольких переменных.
- •Раздел IV. Интегральное исчисление функций одной переменной.
- •Раздел V. Обыкновенные дифференциальные уравнения.
- •Раздел VI. Основы теории вероятностей.
- •Раздел VII. Элементы математической статистики.
- •Литература основная
- •Литература дополнительная
- •Методические указания по изучению курса математики.
- •Методические указания к выполнению контрольной работы №1 Тема №1. Метод координат. Прямая линия.
- •Примеры решения задач.
- •Аналогично, вторая полуплоскость определяется неравенством
- •Определители второго и третьего порядка
- •Примеры решения задач
- •Элементы векторной алгебры.
- •Пример решения задачи.
- •Определить:
- •Вопросы для самопроверки
- •Примеры решения задач
- •Вопросы для самопроверки
- •Дифференциальное исчисление
- •Вопросы для самопроверки
- •Тема №3 Дифференциальное исчисление функции нескольких переменных.
- •Тема №4 Неопределенный интеграл.
- •Определенный интеграл.
- •Примеры вычисления интегралов.
- •Определенный интеграл.
- •Примеры вычисления интегралов.
- •Тема №5 Обыкновенные дифференциальные уравнения 1-го и 2-го порядка.
- •Примеры решения задач.
- •Вопросы для самопроверки
- •Методические указания к выполнению контрольной работы №2. Основы теории вероятностей и элементы математической статистики.
- •Случайные события.
- •Вопросы для самопроверки
- •Примеры решения задач,
- •По таблице (приложение 1 руководства в.Е. Гмурмана) находим, что
- •По таблице (приложение 2 руководства в.Е. Гмурмана) находим
- •Используя формулу для вычисления несмещенного среднего значения х
- •Контрольные задания Задачи для контрольной работы №1. Метод координат. Прямая линия. Вектор.
- •Пределы. Раскрытие простейших неопределенностей.
- •Дифференцирование
- •Неопределенный и определенный интегралы.
- •Дифференциальные уравнения.
- •Контрольная работа №2 по курсу теории вероятностей и математической статистики.
- •Вопросы для подготовки к экзамену по курсу математики
Тема №3 Дифференциальное исчисление функции нескольких переменных.
Э.С. Маркович. ч.1, раздел 6, глава 15, упражнения.
Понятие функции одной переменной не охватывает все зависимости, существующие в природе.
Основная проблема при изучении этой темы возникает в момент дифференцирования указанных функций. Это связано с тем, что при дифференцировании функции по одной переменной все другие переменные предполагаются постоянными величинами. Например,
(x + y)x' = x x' + y x' = 1 + 0 = 1; (xy2) y' = x(y2) y' = 2xy; x y' = 0 ,
y x' = 0
Задача 1. Найти частные производные функции Z = xy.
Решение: Найдем производную функции Z по переменной х. В этом случае при дифференцировании величина у считается постоянной и поэтому: (xy)x' = yxy-1
Аналогично найдем производную функции по у, считая величину х постоянной
(xy)y' = xyln|x|
В естествознании приходится пользоваться эмпирическими формулами, составленными на основе опыта и наблюдений. Один из наилучших методов получения таких формул - это способ наименьших квадратов.
Поясним идею этого способа на примере.
Задача 2. Даны значения переменных величин х и у, полученных в результате опыта:
 х 0 1 2 3 4 5 6
Таблица 1.
х 0 1 2 3 4 5 6
Таблица 1.
у -3 -1 1 3 5 7 9
При этом предполагается, что х и у связаны уравнением
у = ах + b (1)
Требуется найти параметры а и b этого уравнения способом наименьших квадратов.
Решение: Известно, что для определения двух параметров а и b функции (1) способом наименьших квадратов по значениям переменных надо составить и решить систему двух уравнений вида

где n = 7 (число опытов).
Для удобства расчетов составим таблицу 2.
i |
xi |
yi |
xi2 |
xiyi |
1 |
0 |
-3 |
0 |
0 |
2 |
1 |
-1 |
1 |
-1 |
3 |
2 |
1 |
4 |
2 |
4 |
3 |
3 |
9 |
9 |
5 |
4 |
5 |
16 |
20 |
6 |
5 |
7 |
25 |
35 |
7 |
6 |
9 |
36 |
54 |
n ∑ i=1 |
21 |
21 |
91 |
119 |
Составляем систему уравнений:
![]()
Решая эту систему при помощи определителей второго порядка, находим:

Подставляя полученные значения a и b в формулу (I), найдем уравнение прямой
y = 2x – 3,
которое приближенно выражает искомую зависимость между х и у.
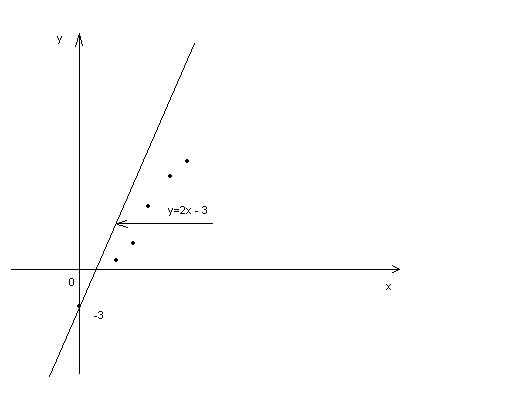
Рис 3.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Что называется функцией двух переменных?
2. Дайте определения частных производных.
3.Как находится экстремум функции нескольких переменных?
4. В чем состоит способ наименьших квадратов построения эмпирических формул?
