§2. Распределение времени ожидания в сож

Пусть - время ожидания обслуживания (время в очереди, затраченное каждым клиентом) - неотрицательная непрерывная случайная величина. - вероятность того, что вызову придется стоять в очереди. - вероятность полной загрузки СМО. Средняя доля времени, в течение которого были заняты все его линии.

Состояния:

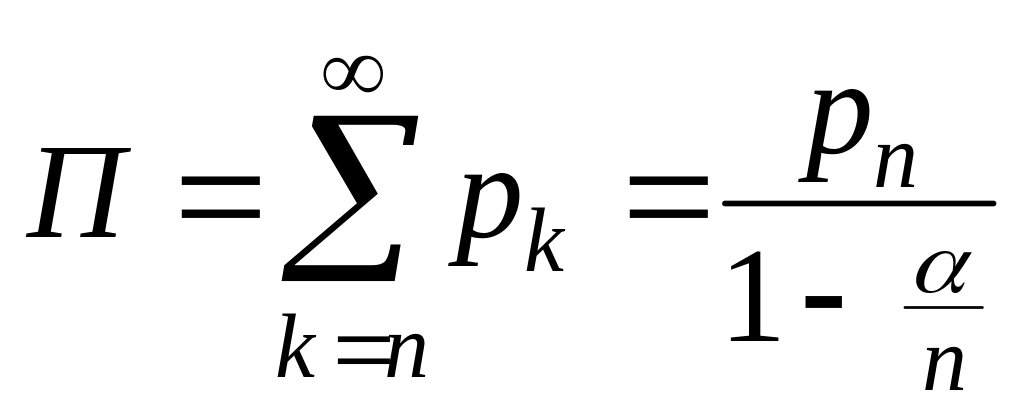(1)

- функция распределения для

Пусть - вероятность при условии того, что вызов застал систему в состоянии

при

(2)

Пусть - длина очереди в состоянии . Тогда - вероятность при условии того, что все линии пучка заняты и имеется вызовов. Ждать больше времени придется, когда за произойдет освобождений линий.

- вероятность того, что за с момента поступления вызова произойдет освобождений.

(то есть освобождений за ). (3)

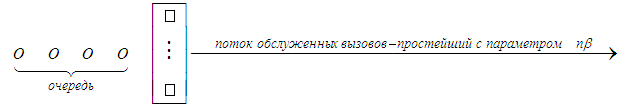
; . (4)

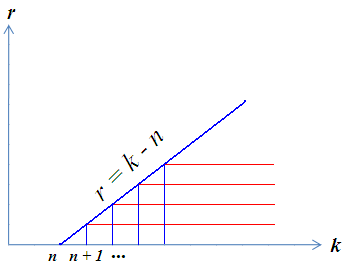
Тогда

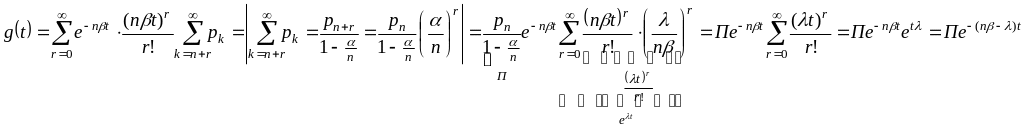
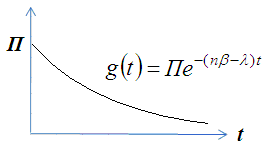
§3. Показатели эффективности сож

1. Среднее число занятых линий

Пусть случайная величина - число занятых линий.

; , так как

Смежные показатели.

а) Среднее число свободных линий:

б) Коэффициент загрузки (линии или СМО)

( - знаменатель геометрической прогрессии).

2. . Смежный показатель .

Замечание: в стационарном режиме для каждого вызова существует две возможности с постоянными вероятностями: попадание в очередь - ;

немедленное обслуживание - .

Простейшие потоки с параметрами и .

; ;

3. Среднее время ожидания обслуживания (среднее время в очереди). - - функция распределения

, поскольку .

, , так как легко показать, что

4. Среднее время пребывания вызова в СМО.

- время пребывания вызова в СМО.

с ростом

5. Средняя длина очереди. - длина очереди.

Состояния:				…
		1	2	…
Вероятности:				…

геометрическая прогрессия

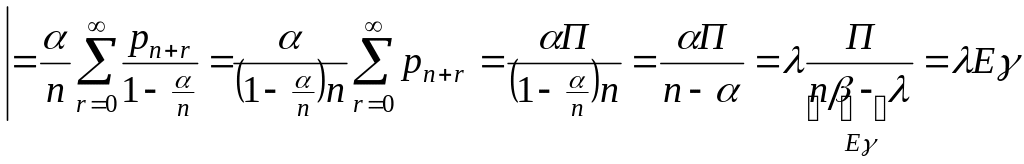
Пример: пусть в среднем имеет место 100 вызовов в час

6 минут = 0,1 часа – среднее время ожидания обслуживания. .

Среднее число вызовов в СМО. Пусть - число вызовов в СМО.

;

§4. Расчёт числа линий

; ,

Подходы для выбора :

1. Алгебраический подход.

Расчёт числа испытательных стендов на заводе.

Линия – испытательный стенд (ИС).

Вызов – изделие, направляемое на контроль.

Поток готовой продукции можно считать неограниченным, где производственный процесс является непрерывным поток изделий на контроль можно считать неограниченным (и непрерывным) и простейшим. .

- время контроля – показательно распределённая случайная величина с параметром .

Обслуживание – контроль.

Требования к СМО и способ их учёта:

Загрузка ИС должна быть достаточно высокой, однако не на 100% (ИС нужен ремонт).

Пусть – вероятность полной загрузки. Пусть . Контроль качества должен осуществляться достаточно быстро. ; ; .

Тогда ;

Пример: пусть ; см.; ; ; .

2. Оптимизационный подход.

, ,

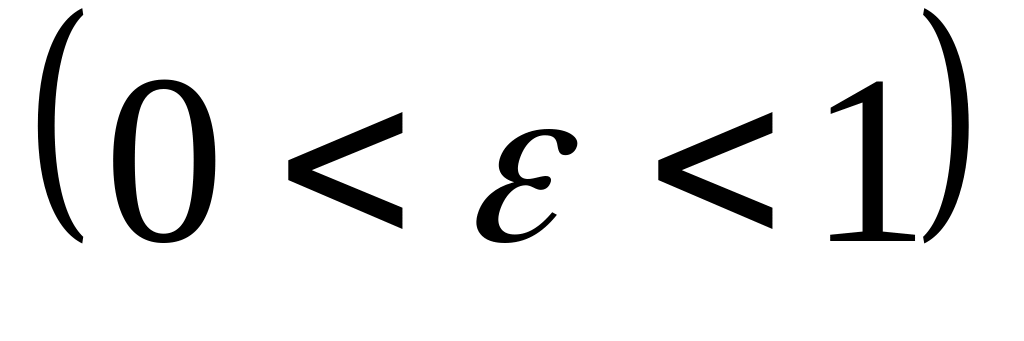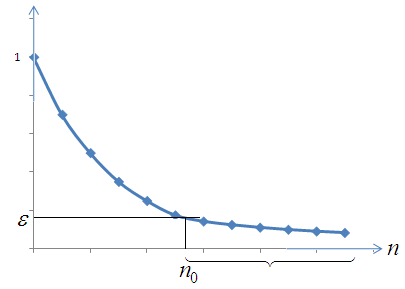
1. Задаётся максимальный уровень полной загрузки - . Требуется найти минимальное число линий, обеспечивающее .

; ;

.

2. - максимальное время, в течение которого вызов может ждать обслуживания.

; .

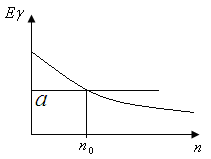
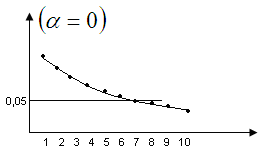
Пример: расчет оптимального числа посадочных полос.

в среднем; каждая полоса способна принимать .

Пусть ; .

;

; ;