§ 6. Упорядоченный пучок групп линий

I. Организация обслуживания.

– число линий в группе с номером .

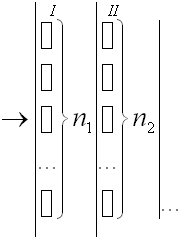
Входящий поток – простейший с параметром . Время обслуживания распределено показательно с параметром .

Пусть - суммарное число линий в первых группах.

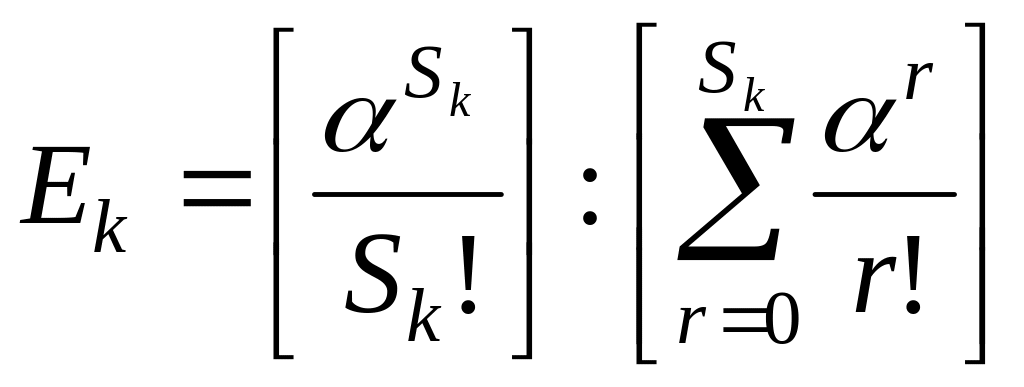, где – количество групп.

3 линии:

_{а) ;}

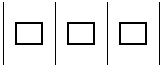б) ;

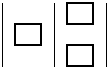в) ;

г) .

- вероятность пройти без обслуживания первые групп.

Постановка экстремальной задачи

, ,

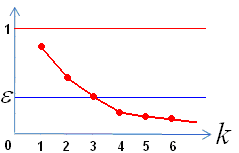
Примеры упорядоченных пучков групп линий:

1) Защита объекта. Вызов – ракета. Простейший поток ракет. Пусть – количество ПРУ в -ой зоне. Обслуживание – уничтожение ракеты.

– ракета преодолела зону 1. I

– I, II; – I, II, III; _.

Пусть ; ; .

2) Окраска изделий. Существует 2 цеха – основной и дополнительный

Цеха

Поток изделий, поступающих на окраску, считается простейшим с параметром .

изделий/смену; изделий/смену.

Вероятность того, что изделие не будет окрашено в основном цеху.

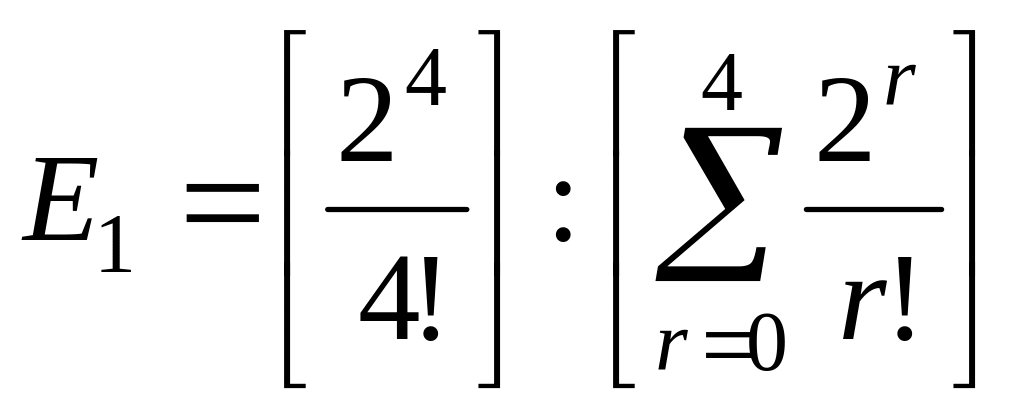
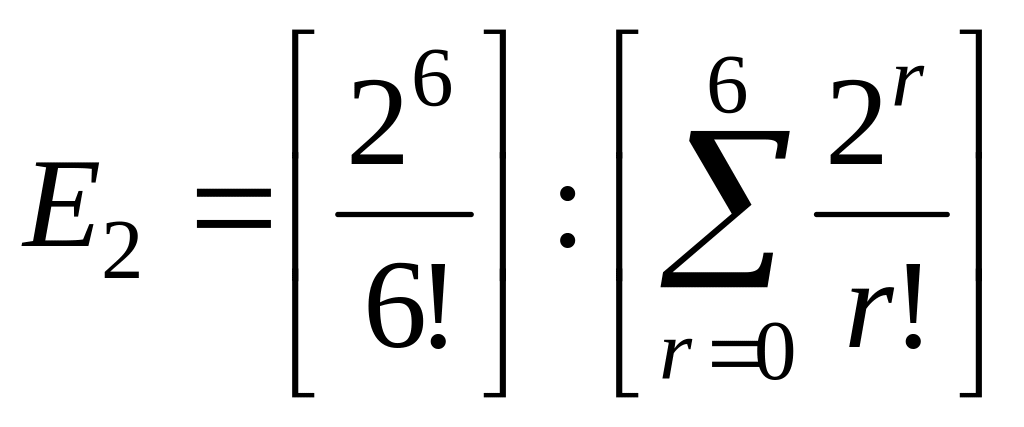; пусть

Вероятность того, что изделие, не окрашенное в основном цехе, не будет окрашено и в дополнительном. ; пусть

Тема 3. Системы с ожиданием

Пусть - количество линий в пучке.

Входящий поток - простейший с параметром ; время обслуживания распределено показательно с параметром . Множество состояний СМО – счётно.

- состояния СМО на .

а) – состояние СМО можно определить либо как количество занятых линий, либо как количество вызовов на обслуживании.

свободных линий.

б) , то есть заняты все линий пучка, вызовов в очереди.

§ 1. Пгр и стационарное решение

- состояние СМО на момент времени . Пусть - марковский ПГР.

Пусть ; ; . (1)

Доказательство: ◄

I. - марковский. Существует

II. - ПГР. Параметры его соответствуют указанным в (1).

Переходные вероятности:

1)

2)

(2)

Докажем (2):

Если

- ровно одно освобождение.

3)

- 0 вызовов для простого потока

- 0 освобождений.

Стационарное решение.

(*) если , , получаем - геометрическую прогрессию. Пусть знаменатель равен

Если , ; (3)

.

Значит, (4)

остается неизвестным.

если , то расх., с течением времени очередь только растет, поскольку СМО не справляется. Считаем, что ряд сходится.

(5) 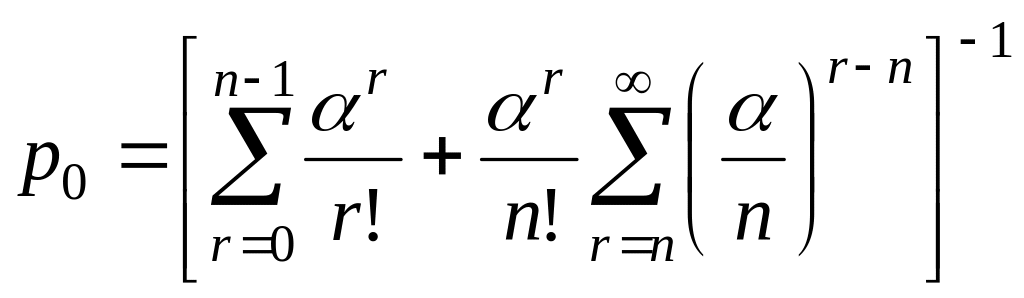; по формуле геометрической прогрессии , поэтому теперь (если )

– вероятность того, что все линии свободны.

для более общего случая получаем, подставляя в формулы (3) и (4) для .

Фиксируем и смотрим, как себя ведет при .

Свойства последовательности

1) . образуют геометрическую прогрессию со знаменателем , так как . .

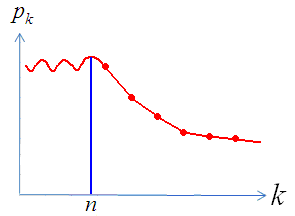
2) Чем больше номер состояния, тем меньше его вероятность. . С ростом вероятности больших размеров очереди малы.

;

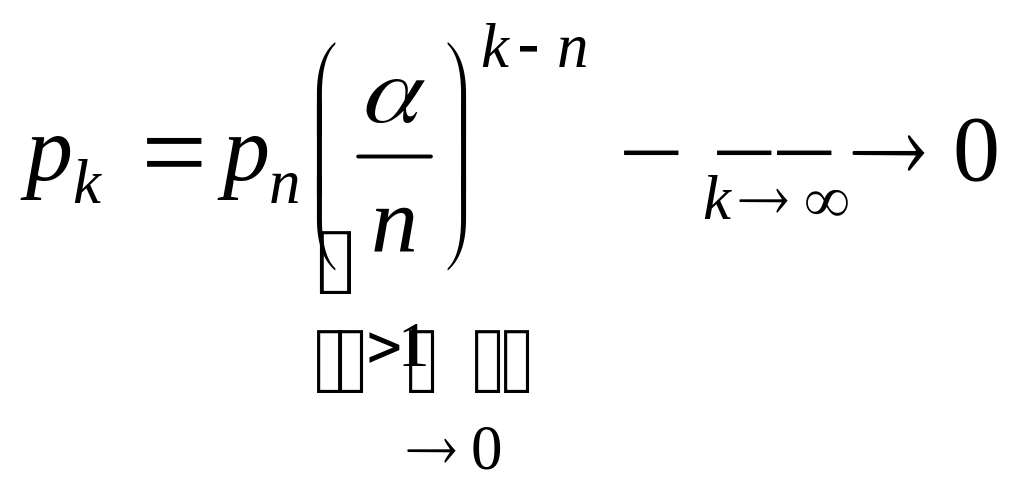Замечания:

1. Физический смысл условия

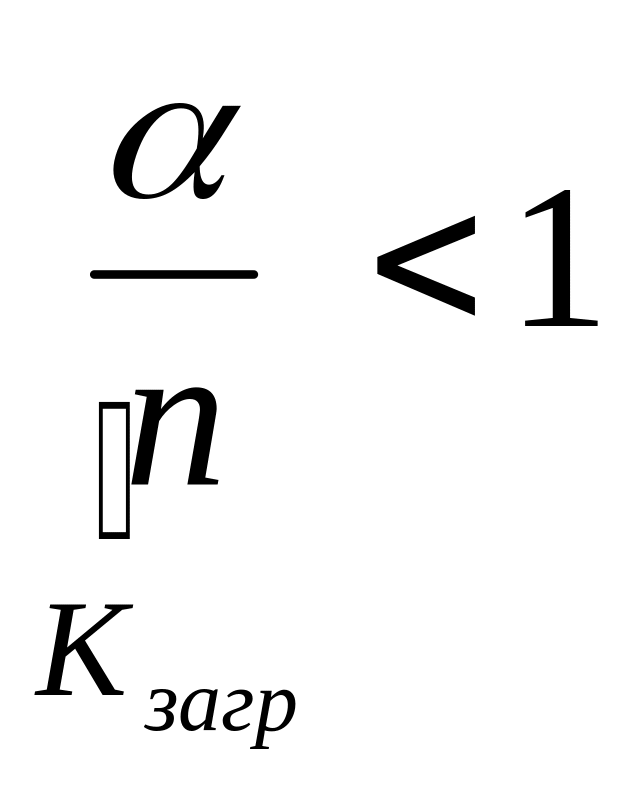
- среднее число вызовов, которое система может обслужить. В среднем поступает вызовов в единицу времени.

Очередь неограниченно растет. Тогда (а не только когда )

Пример: прием больных врачом.

Пусть (врач); заполнение карточки - в среднем 20 минут . У врача пропускная способность 3 человека в час. челов./час. На четырехчасовой рабочий день 12 человек.