§ 4. Формулы Эрланга для бесконечного пучка и практические приложения
Пучок бесконечен нет ни отказов, ни ожидания.
Входящий поток – простейший с параметром .
Время обслуживания распределено показательно с параметром .
Состояния СМО можно понимать как качество вызовов на обслуживании
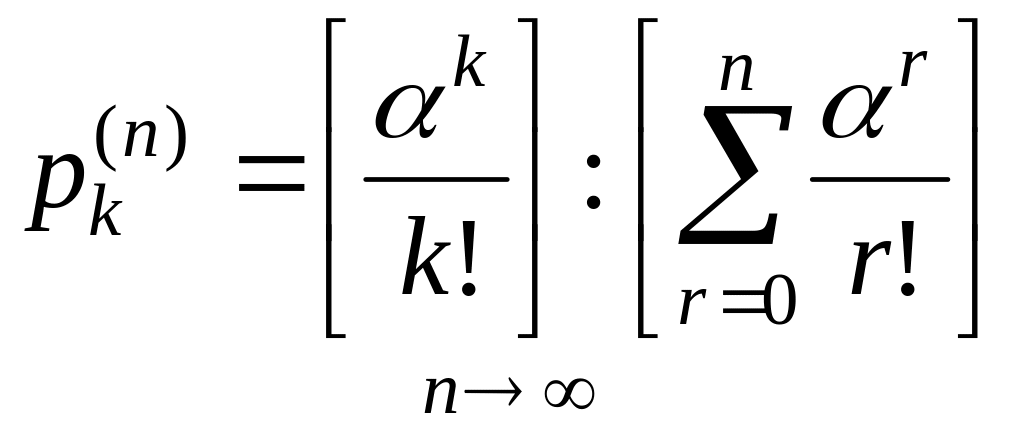
Формулы Эрланга для бесконечного пучка.
0, 1, 2, …
, …
Вероятности:
, 
, 
, …
, …
- показатель эффективности.
для конечного пучка.
,
так как
.
Для систем с отказом формулы Эрланга
остаются верными и для
распределения
.
Приложения:
Доставка телеграмм. СМО – телеграф, пучок линий – совокупность почтальонов.
Допущения:
Пусть каждый почтальон одновременно доставляет только одну телеграмму.
Считаем, что телеграмма доставляется немедленно по ее получении телеграфом должно быть достаточно много почтальонов. Поток телеграмм можно считать простейшим с параметром
за
часов поступает ровно
телеграмм с вероятностью
;
.
– время доставки телеграммы и возвращения почтальона – случайная величина. Вид распределения не имеет значения.
Какова вероятность того, что в пути находится одновременно почтальонов?
Ремонт автомашин. СМО – совокупность ремонтных мастерских.
Вызов – автомашина, требующая ремонта. Обслуживание – ремонт. Пусть ремонт начинается немедленно по выходу машины из строя. Поток поломок – простейший с параметром .
; - среднее время ремонта автомашины.
Пусть
авт./сут.;
сут.
.
а) Среднее число автомашин, находящееся в ремонте, равно .
б) Вероятность того, что все машины
исправны, равна
.
§ 5. Упорядоченный пучок линий
Пример: упаковочный цех с упаковочными автоматами.
Входящий поток – простейший с параметром .
Время обслуживания – показательно распределено с параметром .
Рассмотрим частичный пучок длины
(из первых «
»
линий).
(пучок конечный).
–
(если пучок бесконечен).
Пусть
– вероятность отказа на пучке длины
.
– событие, состоящее в том, что на
-ой
линии не осуществилось обслуживание.
– средняя доля времени, когда в системе
вызовов ≡ средняя доля вызовов,
получающих отказ в обслуживании.
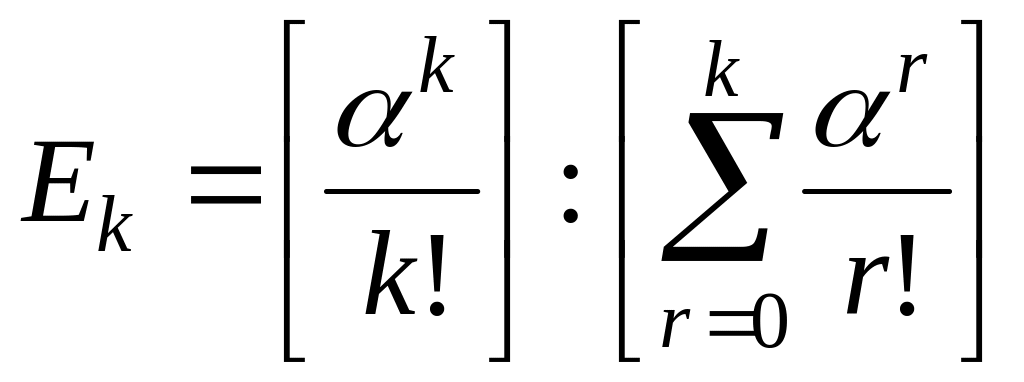
– вероятность того, что вызов
будет обслужен на какой-либо из первых
линий.
Найдем закон распределения номера линии, на которой осуществляется обслуживание вызова:
Обслуживание на
-ой
линии
1, 2, …,
,
…
Найти
- ?
Пусть
1 2 …
Наиболее интенсивным будет поток на первую линию.
Пусть
- интенсивность стационарного потока,
пущенного на
-ю
линию.
- интенсивность входящего потока.
для
- среднее число вызовов в единицу времени.
|
вероятности исходов |
интенсивности |
отказ на частичном пучке |
|
|
обслуживание |
|
|
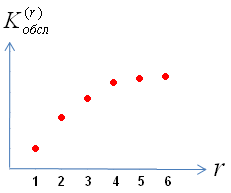
Поток все полнее обслуживается с повышением номера линии (полнота обслуживания измеряется коэффициентом обслуживания
,
).
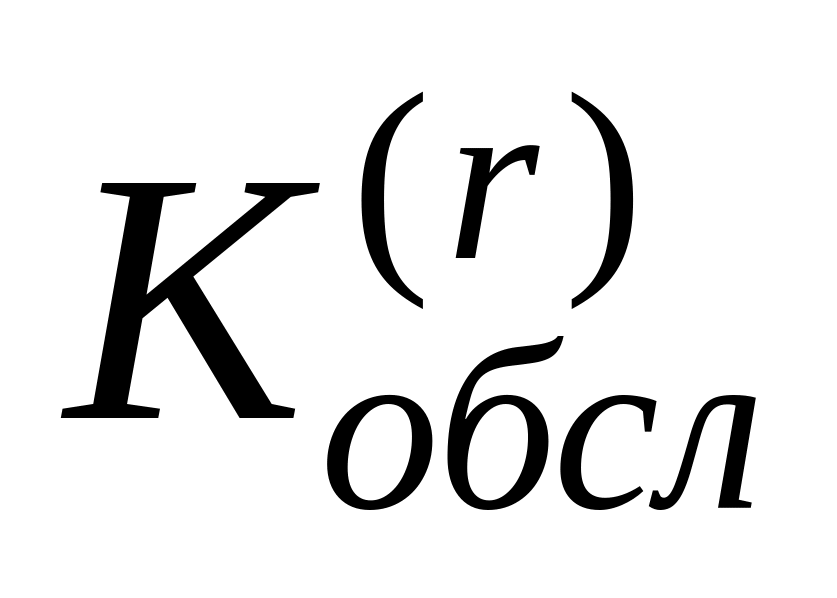а)
- вероятность отказа на линии
при условии того, что вызов поступил
на эту линию.
через
и
.
через
;
пусть
;
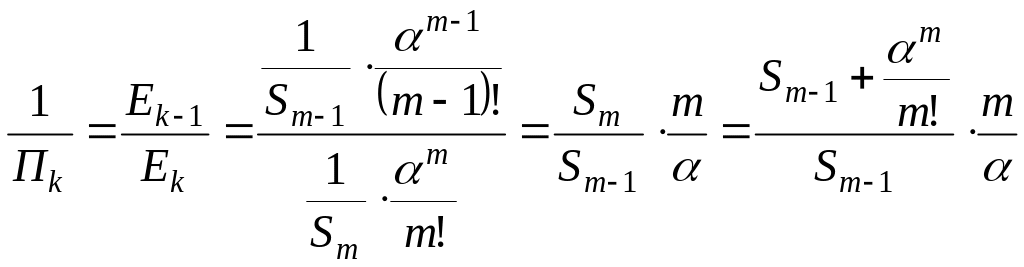
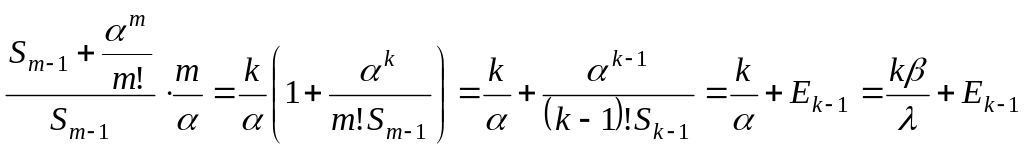б)
Обслуживается
(среднее число обслуженных вызовов за единицу времени).
- вероятность того, что вызов будем
обслужен на
-ой
линии при условии того, что вызов
поступил на
-ю
линию.