
- •Теория массового обслуживания
- •Введение в тмо
- •§ 1. О задачах тмо
- •Основные задачи тмо
- •Области применения тмо
- •§ 2. Необходимость вероятностного моделирования (на примере расчета числа причалов в порту).
- •§ 3. Основные понятия и допущения.
- •Допущения в тмо:
- •Тема 1. Основы тмо
- •§ 1. Понятие о случайном процессе и его марковости
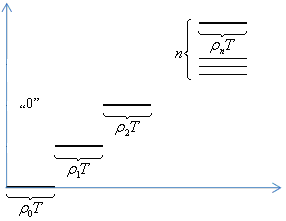
- •§ 2. Понятие о процессах гибели и размножения (пгр). Стационарное решение и его интерпретация.
- •§ 3. Задание потока вызовов
- •§ 4. Простейший поток вызовов
- •Графики
- •§ 5. Свойства показательного распределения разговора
- •§ 6. Марковость в задаче Эрланга
- •§ 7. Выходящий поток из непрерывно загруженной смо
- •Тема 2. Системы с отказом и смежные с ними
- •§ 1. Пгр и стационарное решение для системы с отказом
- •§ 2. Показатели эффективности сот
- •§ 3. Оптимальное число линий в сот
- •§ 4. Формулы Эрланга для бесконечного пучка и практические приложения
- •Приложения:
- •§ 5. Упорядоченный пучок линий
- •§ 6. Упорядоченный пучок групп линий
- •Тема 3. Системы с ожиданием
- •§ 1. Пгр и стационарное решение
- •§2. Распределение времени ожидания в сож
- •§3. Показатели эффективности сож
- •§4. Расчёт числа линий
- •§ 5. Практические приложения модели сож
- •II. Расчет объема памяти информационно-логической машины (илм).
- •Оптимальная интенсивность пополнения запаса товаров в магазине.
- •Тема 4. Системы с ограниченной очередью
- •§ 1. Модель, пгр, стационарное решение и распределение времени ожидания для систем с ограниченной очередью
- •Распределение времени ожидания.
- •§2. Показатели эффективности соч
- •Вероятность отказа
- •Среднее число занятых линий.
- •§3. Оптимальное число линий в соч (на примере расчета оптимального размера максимального запаса товара при задалживании спроса)
- •§4. Практические приложения
- •Срочная доставка грузов
- •Использование уличных телефонных кабин
- •Тема 5. Замкнутые смо (циклические, сож при ограниченном входящем потоке)
- •§1. Модель замкнутой смо
- •§2. Пгр и стационарное решение (для замкнутой смо)
- •§3. Показатели эффективности замкнутых смо
- •§4. Оптимальное число линий в замкнутых смо (на примере расчета оптимального числа линий починки станков-автоматов)
- •§5. Практические приложения модели замкнутых смо
§ 2. Показатели эффективности сот
1. Вероятность отказа
![]() застать все линии занятыми
полной загрузки СОТ.
застать все линии занятыми
полной загрузки СОТ.
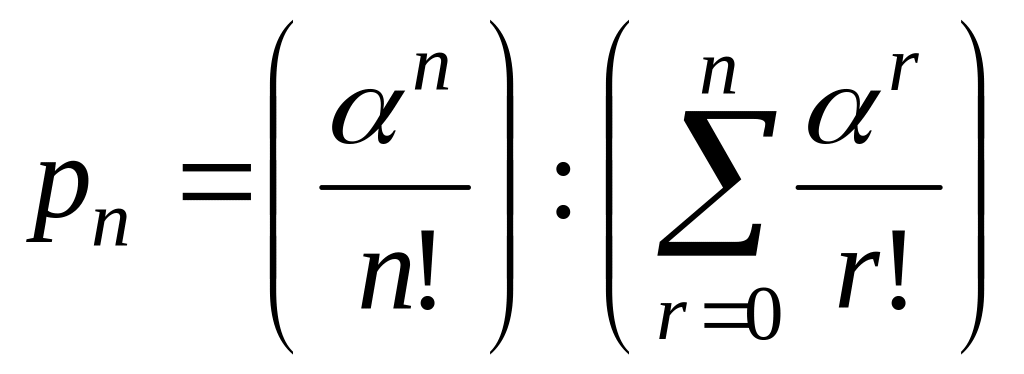
![]() Рассмотрим
Рассмотрим
![]()
С ростом
![]() уменьшается.
уменьшается.
![]() .
Кроме того,
.
Кроме того,
![]() ,
то есть если
велико,
настолько мало, что ей можно пренебречь
и считать СМО безотказной.
,
то есть если
велико,
настолько мало, что ей можно пренебречь
и считать СМО безотказной.
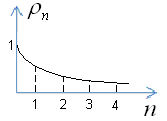
Для любого вызова возможны два исхода:
либо отказ
![]() ,
либо обслуживание
,
либо обслуживание
![]() .
.
![]() - количество отказов за
- количество отказов за
![]() ;
;
![]() - количество обслуженных вызовов за
;
- количество обслуженных вызовов за
;
![]() - простейший входящий поток с параметром
.
Тогда
- простейший входящий поток с параметром
.
Тогда
![]() .
.
![]() ,
,
![]() - простейшие с параметрами
- простейшие с параметрами
![]() и
и
![]() .
.
Следствия:
a) Новая интерпретация
и
![]() :
[средняя доля отказов] = [среднее число
отказов (за единицу времени)]:[среднее
число поступивших вызовов (за единицу
времени)] = │поскольку
- простейший поток│=
:
[средняя доля отказов] = [среднее число
отказов (за единицу времени)]:[среднее
число поступивших вызовов (за единицу
времени)] = │поскольку
- простейший поток│=
![]() .
.
Средняя доля обслуженных вызовов
аналогично равна
![]() - коэффициент обслуживания.
- коэффициент обслуживания.
Пусть поступило
вызовов. Тогда
![]() - среднее число отказов, а
- среднее число отказов, а
![]() - среднее число обслуженных вызовов.
- среднее число обслуженных вызовов.
б)
![]() {
{![]() вызовов получат отказ за период
}.
вызовов получат отказ за период
}.
![]()
![]() {
вызовов будет принято на обслуживание
за период
}.
{
вызовов будет принято на обслуживание
за период
}.
![]()
в)
![]() ;
;
![]()
2. Среднее число занятых линий.
![]()
![]()
Интерпретация:
1.
![]() [интенсивность
потока обслуженных вызовов]:[интенсивность
потока обслуживания одной линии].
[интенсивность
потока обслуженных вызовов]:[интенсивность
потока обслуживания одной линии].
![]() ,
где
- пропускная способность системы.
,
где
- пропускная способность системы.
2.
![]() - среднее число обслуженных вызовов за
- среднее число обслуженных вызовов за
![]() ;
- среднее число обслуженных вызовов за
единицу времени;
;
- среднее число обслуженных вызовов за
единицу времени;
![]() .
.
Смежные с
![]() показатели.
показатели.
1. Среднее число свободных линий.
Пусть
![]() - число свободных линий,
- число свободных линий,
![]() .
.
![]() .
.
2. Коэффициент загрузки (линии, СМО)
![]()
![]() [суммарное
время работы (за
[суммарное
время работы (за
![]() )]:[суммарный
фонд работы всех линий (за
)]
)]:[суммарный
фонд работы всех линий (за
)]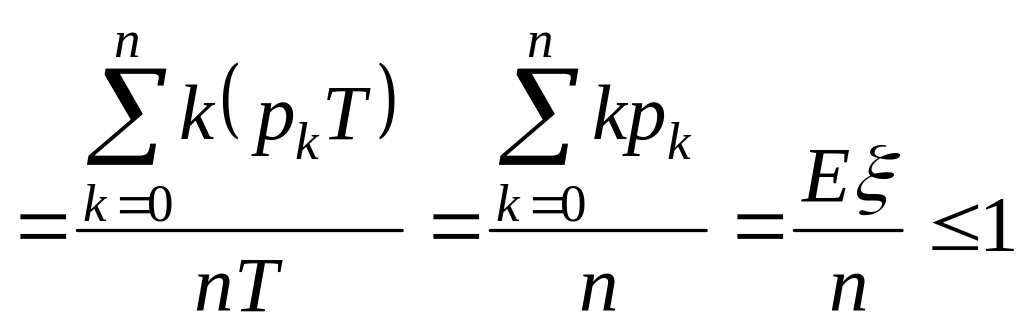 .
.
Также
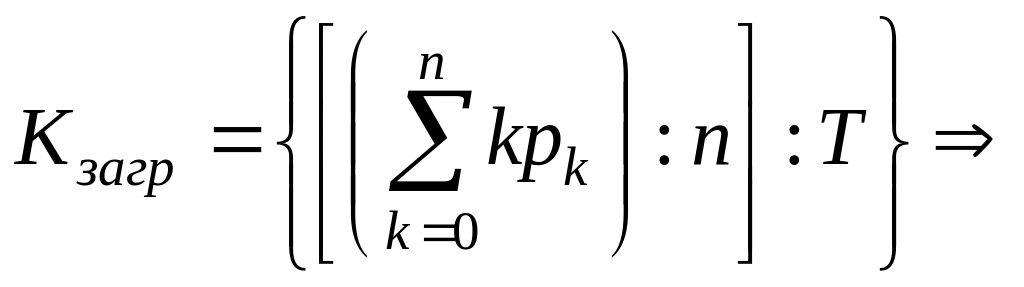 среднее время, отработанное одной
линией за
,
пропорционально длине
.
Коэффициентом пропорциональности в
данном случае является
среднее время, отработанное одной
линией за
,
пропорционально длине
.
Коэффициентом пропорциональности в
данном случае является
![]() .
.
Коэффициент простоя
![]() - средняя доля свободного времени
(линии, СМО).
- средняя доля свободного времени
(линии, СМО).
![]() .
.
§ 3. Оптимальное число линий в сот
1. Пусть задается уровень обслуживания
![]() - максимальное значение доли вызовов,
которые могут получать отказ в данной
СМО. Пусть
- максимальное значение доли вызовов,
которые могут получать отказ в данной
СМО. Пусть
![]() ,
это значит, что не больше 10% вызовов
могут получать отказ.
,
это значит, что не больше 10% вызовов
могут получать отказ.
![]()
2. Пусть
- средняя плата за обслуживание;
![]() - штраф за отказ в обслуживании;
- штраф за отказ в обслуживании;
![]() - оплата труда линии за единицу времени
ее работы. Средняя прибыль
- оплата труда линии за единицу времени
ее работы. Средняя прибыль
![]() .
Определить число линий в данной системе,
при котором
является максимальным.
.
Определить число линий в данной системе,
при котором
является максимальным.
![]()
![]()
3.
![]()
4. Оптимальный размер максимального числа товаров в магазине при отсутствии задалживания спроса.
Допущения:
Поток покупателей является простейшим с параметром (человек в неделю). ,
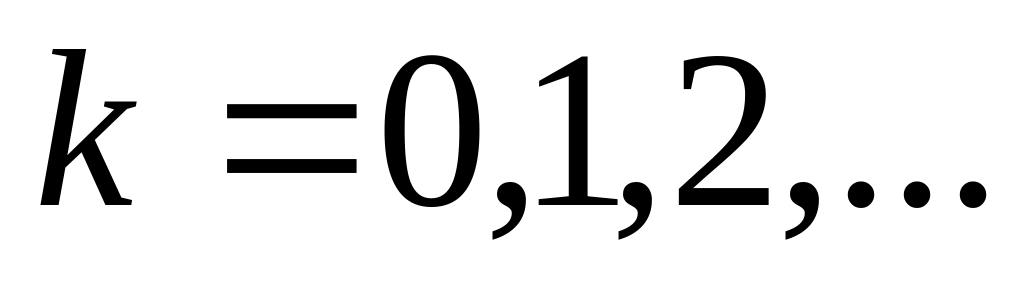
В одни руки отпускается только одна единица товаров
 - вероятность того, что спрос будет
предъявлен за
единиц времени на
единиц товара.
- вероятность того, что спрос будет
предъявлен за
единиц времени на
единиц товара.Как только происходит продажа единицы товара, сразу подается заявка на замену ее другой единицей [количество товара в магазине] + [количество заявок]
 .
можно понимать либо как максимальный
размер товара, либо как максимальное
количество заявок.
.
можно понимать либо как максимальный
размер товара, либо как максимальное
количество заявок.Время выполнения заявки - непрерывная случайная величина, распределенная по показательному закону с параметром .
Если товар в магазине отсутствует, то покупатель получает отказ и уходит.
Пусть а – доход от продажи единицы товара за вычетом издержек выполнения заказа по доставке товара в магазин.
Пусть b – издержки
хранения единицы товара в течение
промежутка времени
![]() .
.
Средняя прибыль
![]()
Линия – ячейка. Линия занята – ячейка
пуста,
![]() заявка
заявка
![]() .
Линия свободна – ячейка заполнена
.
Линия свободна – ячейка заполнена
![]() .
Всего n линий.
.
Всего n линий.
Что есть состояние СМО?
![]()
Обслуживание – выполнение заявки.
![]() – на момент
подано
заявок.
– на момент
подано
заявок.
![]() -
средняя прибыль за
.
-
средняя прибыль за
.
![]() (
– не учитывает
)
(
– не учитывает
)
![]() ;
;
![]()
![]() (b учитывает
)
(b учитывает
)
![]() (
(![]() ,
где
– себестоимость,
,
где
– себестоимость,
![]() ).
).
