
- •Теория массового обслуживания
- •Введение в тмо
- •§ 1. О задачах тмо
- •Основные задачи тмо
- •Области применения тмо
- •§ 2. Необходимость вероятностного моделирования (на примере расчета числа причалов в порту).
- •§ 3. Основные понятия и допущения.
- •Допущения в тмо:
- •Тема 1. Основы тмо
- •§ 1. Понятие о случайном процессе и его марковости
- •§ 2. Понятие о процессах гибели и размножения (пгр). Стационарное решение и его интерпретация.
- •§ 3. Задание потока вызовов
- •§ 4. Простейший поток вызовов
- •Графики
- •§ 5. Свойства показательного распределения разговора
- •§ 6. Марковость в задаче Эрланга
- •§ 7. Выходящий поток из непрерывно загруженной смо
- •Тема 2. Системы с отказом и смежные с ними
- •§ 1. Пгр и стационарное решение для системы с отказом
- •§ 2. Показатели эффективности сот
- •§ 3. Оптимальное число линий в сот
- •§ 4. Формулы Эрланга для бесконечного пучка и практические приложения
- •Приложения:
- •§ 5. Упорядоченный пучок линий
- •§ 6. Упорядоченный пучок групп линий
- •Тема 3. Системы с ожиданием
- •§ 1. Пгр и стационарное решение
- •§2. Распределение времени ожидания в сож
- •§3. Показатели эффективности сож
- •§4. Расчёт числа линий
- •§ 5. Практические приложения модели сож
- •II. Расчет объема памяти информационно-логической машины (илм).
- •Оптимальная интенсивность пополнения запаса товаров в магазине.
- •Тема 4. Системы с ограниченной очередью
- •§ 1. Модель, пгр, стационарное решение и распределение времени ожидания для систем с ограниченной очередью
- •Распределение времени ожидания.
- •§2. Показатели эффективности соч
- •Вероятность отказа
- •Среднее число занятых линий.
- •§3. Оптимальное число линий в соч (на примере расчета оптимального размера максимального запаса товара при задалживании спроса)
- •§4. Практические приложения
- •Срочная доставка грузов
- •Использование уличных телефонных кабин
- •Тема 5. Замкнутые смо (циклические, сож при ограниченном входящем потоке)
- •§1. Модель замкнутой смо
- •§2. Пгр и стационарное решение (для замкнутой смо)
- •§3. Показатели эффективности замкнутых смо
- •§4. Оптимальное число линий в замкнутых смо (на примере расчета оптимального числа линий починки станков-автоматов)
- •§5. Практические приложения модели замкнутых смо
§ 6. Марковость в задаче Эрланга
Входящий поток - простейший, время обслуживания - показательное, случайный процесс – марковский.
Доказательство:
◄
![]() ;
;
![]() ;
;
![]() ;
- последующие моменты.
;
- последующие моменты.
3 фактора, определяющих .
Моменты окончания тех разговоров, которые ведутся в момент . Имеет место независимость от прошлого. Длины разговоров распределены экспоненциально
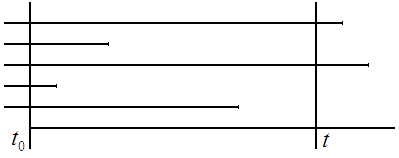
Моменты поступления новых вызовов в интервале
 .
.
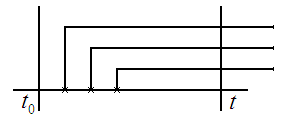
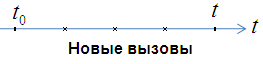
Независимость от прошлого вытекает из того, что входящий поток простейший марковский.
Моменты окончания новых разговоров. Раз вызовы поступили после разговоры заканчиваются или нет независимо от ►.
§ 7. Выходящий поток из непрерывно загруженной смо
I.
![]() .
.
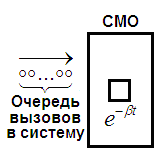
Пусть СМО загружена непрерывно. Тогда поток обслуженных вызовов является простейшим с параметром .
◄ Поток освобождений линии является
марковским, так как количество
освобождений в промежутке не зависит
от количества освобождений до этого
промежутка.
![]() для
,
длины разговоров независимы друг от
друга, все
для
,
длины разговоров независимы друг от
друга, все
![]() распределены по показательному закону
распределены по показательному закону
![]() получаем простейший поток с параметром
.
получаем простейший поток с параметром
.
![]() - вероятность
освобождений за промежуток длины
.
- вероятность
освобождений за промежуток длины
.
![]()
Пример: Пусть - время исправной работы прибора. распределено по показательному закону с параметром . После поломки прибор заменяется на новый (такой же). - вероятность, что за время произойдет ровно поломок. Линия – условное место, занимаемое прибором.
II. линий.
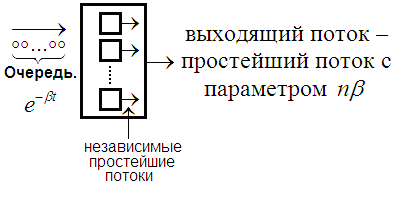
![]()
Тема 2. Системы с отказом и смежные с ними
Пусть - число линий в пучке.
Состояния СМО:
 ;
;

Всего состояний СМО
![]() .
.
Допущения и исходные данные
Входящий поток – простейший с параметром , время обслуживания имеет показательное распределение с параметром .
§ 1. Пгр и стационарное решение для системы с отказом
I. ПГР
Утверждение: В случае системы с отказом
(СОТ) состояние СМО на момент времени
есть марковский ПГР с параметрами
![]()
![]() ;
;
![]()
![]() .
.
То, что - марковский, вытекает из теоремы в § 7.
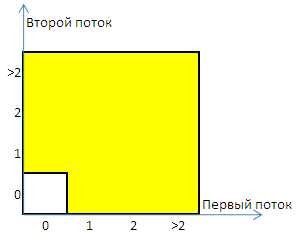
- ПГР. Рассмотрим два потока: наш входящий поток
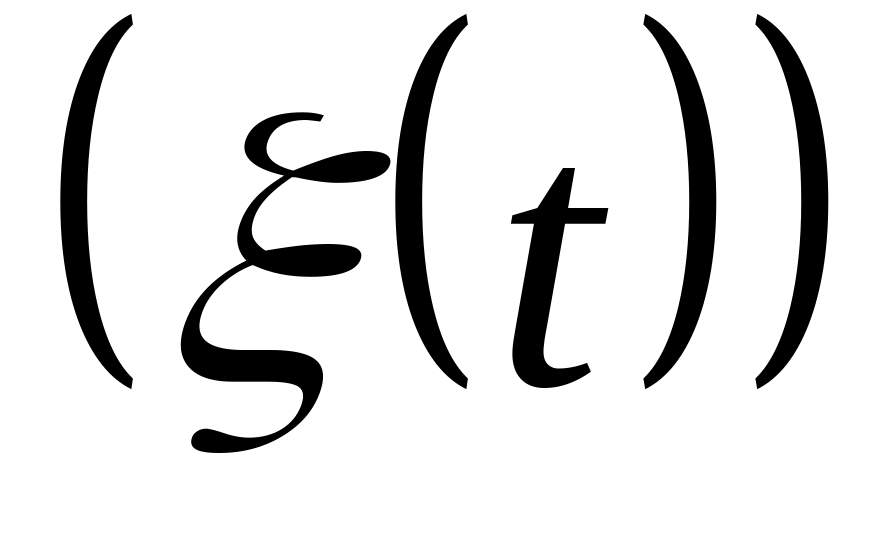 и поток освобождений линий (обслуженных
вызовов)
и поток освобождений линий (обслуженных
вызовов)
 .
.
Для потока
![]()
![]() (1)
(1)
![]() - вероятность того, что в промежутке
будет не менее одного вызова.
- вероятность того, что в промежутке
будет не менее одного вызова.
![]() (2)
(2)
![]() (3)
(3)
![]()
Замечание 1: Если
![]() - ординарный поток. Физический смысл
ординарности – вызовы поступают
поодиночке.
- ординарный поток. Физический смысл
ординарности – вызовы поступают
поодиночке.
Замечание 2: Третье определение простейшего потока:
Поток вызовов называется простейшим, если он:
Процесс без последействия (марковский).
Стационарный.
Ординарный.
Можно проверить, что это определение простейшего потока равносильно двум другим.
Для выходящего потока (вероятности
обозначим
![]() ):
):
Если в данный момент линия занята, то за промежуток она:
Не освободится с вероятностью
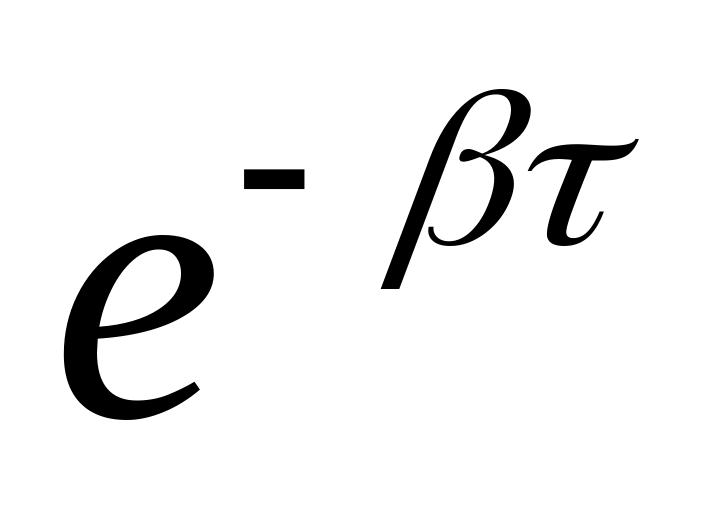 .
.Освободится с вероятностью
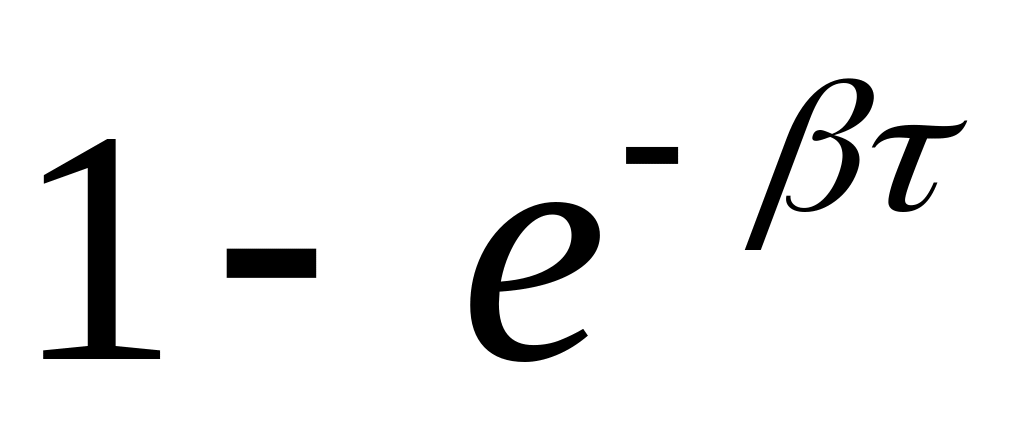 .
.
Если линий пучка в данный момент заняты, то вероятности того, что за промежуток :
Ни одна не освободится.
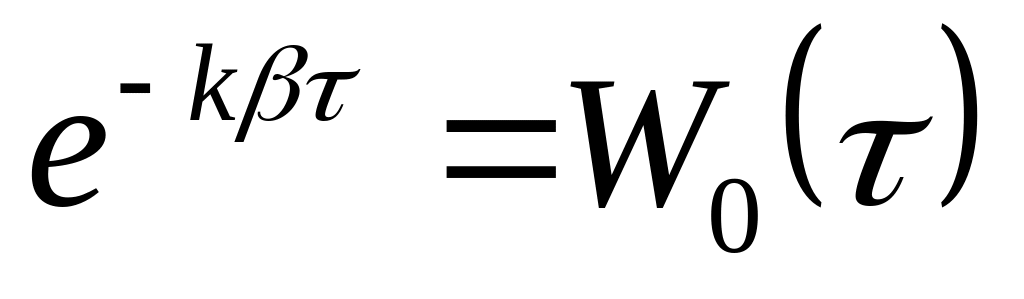 (5)
(5)Освободится по крайней мере одна из них.
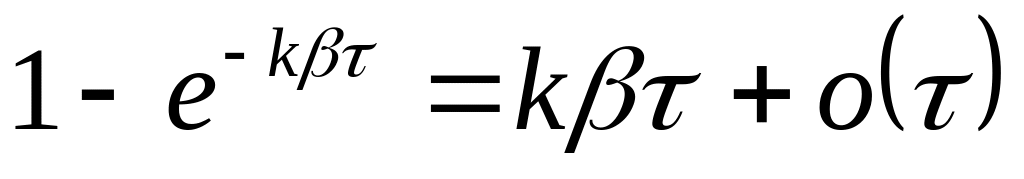 (6)
(6)Освободится только одна из них.
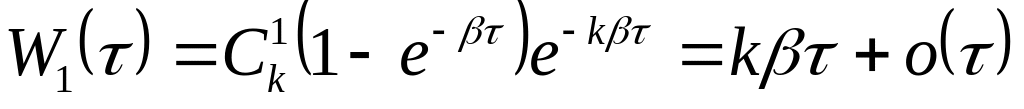 (7)
(7)Освободится больше одной из них.
 (8)
(8)
определяется поступлением вызовов и освобождением – элементарными событиями.
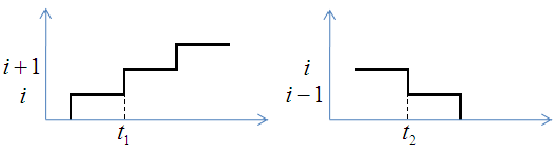
Для элементарных событий вероятность
наступления хотя бы одного из них равна
![]() ;
;
![]()
![]()
1.
![]() за
.
за
.
![]() ,
где
,
где
![]() по (3) (5).
по (3) (5).

2.
![]() за
.
за
.
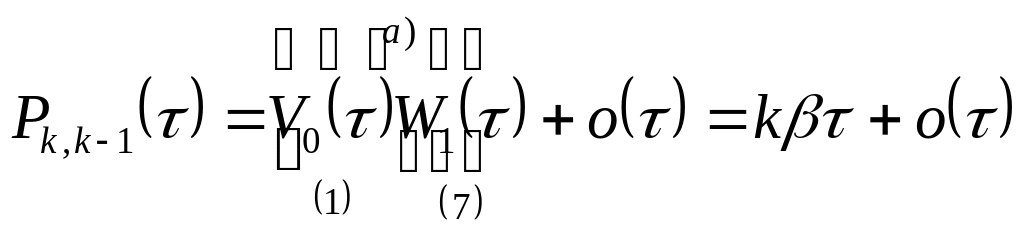 ,
где
,
где
![]() .
.

3.
![]() .
.![]() ,
что и требовалось доказать
- ПГР.
,
что и требовалось доказать
- ПГР.
Стационарные решения.
![]() .
Подставляем сюда значения параметров
и многократно используем реккурентные
соотношения.
.
Подставляем сюда значения параметров
и многократно используем реккурентные
соотношения.
![]() ;
;
![]() ;
;
![]() ;
Пусть
;
Пусть
![]() ;
;
![]() .
.
Нормировочное условие
![]()
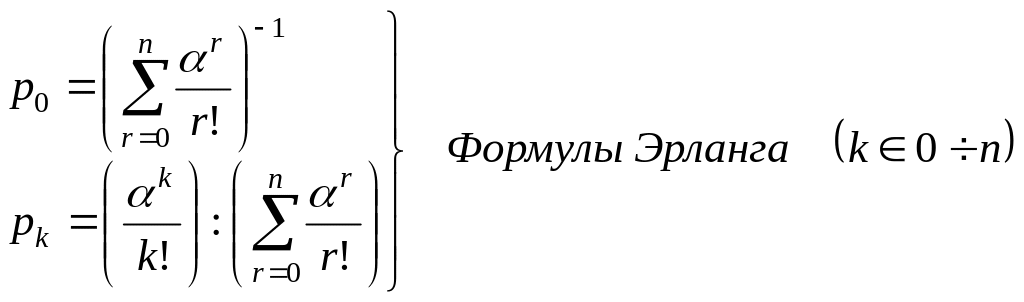
Пусть
![]() - число вызовов в системе.
- число вызовов в системе.
![]()
![]() - по формулам Эрланга.
- по формулам Эрланга.
Формулы Эрланга получены в предположении
о показательном распределении длин
разговоров. Как показал профессор
Севастьянов, они сохраняются при любом
законе распределения длин разговоров.
Но возникает вопрос: откуда взять
![]() откуда взять
откуда взять
![]() ?
?
![]()
