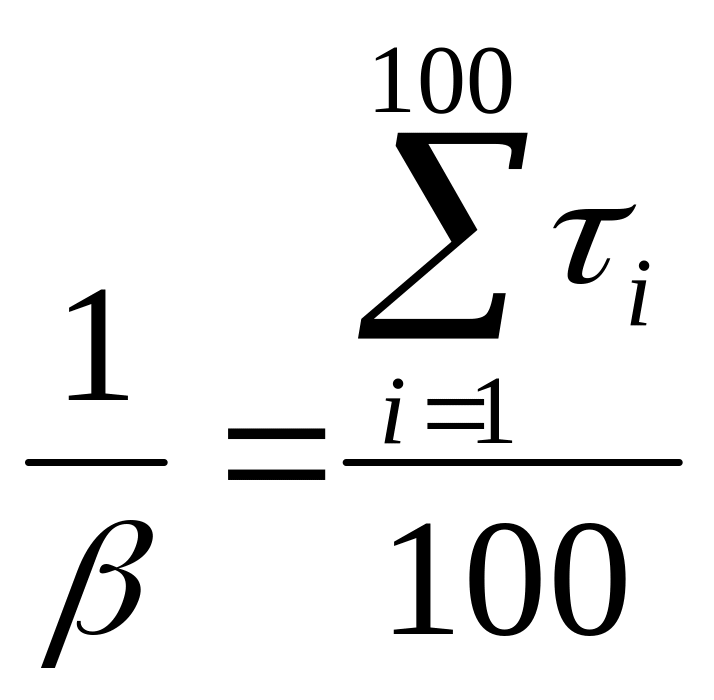- •Теория массового обслуживания
- •Введение в тмо
- •§ 1. О задачах тмо
- •Основные задачи тмо
- •Области применения тмо
- •§ 2. Необходимость вероятностного моделирования (на примере расчета числа причалов в порту).
- •§ 3. Основные понятия и допущения.
- •Допущения в тмо:
- •Тема 1. Основы тмо
- •§ 1. Понятие о случайном процессе и его марковости
- •§ 2. Понятие о процессах гибели и размножения (пгр). Стационарное решение и его интерпретация.
- •§ 3. Задание потока вызовов
- •§ 4. Простейший поток вызовов
- •Графики
- •§ 5. Свойства показательного распределения разговора
- •§ 6. Марковость в задаче Эрланга
- •§ 7. Выходящий поток из непрерывно загруженной смо
- •Тема 2. Системы с отказом и смежные с ними
- •§ 1. Пгр и стационарное решение для системы с отказом
- •§ 2. Показатели эффективности сот
- •§ 3. Оптимальное число линий в сот
- •§ 4. Формулы Эрланга для бесконечного пучка и практические приложения
- •Приложения:
- •§ 5. Упорядоченный пучок линий
- •§ 6. Упорядоченный пучок групп линий
- •Тема 3. Системы с ожиданием
- •§ 1. Пгр и стационарное решение
- •§2. Распределение времени ожидания в сож
- •§3. Показатели эффективности сож
- •§4. Расчёт числа линий
- •§ 5. Практические приложения модели сож
- •II. Расчет объема памяти информационно-логической машины (илм).
- •Оптимальная интенсивность пополнения запаса товаров в магазине.
- •Тема 4. Системы с ограниченной очередью
- •§ 1. Модель, пгр, стационарное решение и распределение времени ожидания для систем с ограниченной очередью
- •Распределение времени ожидания.
- •§2. Показатели эффективности соч
- •Вероятность отказа
- •Среднее число занятых линий.
- •§3. Оптимальное число линий в соч (на примере расчета оптимального размера максимального запаса товара при задалживании спроса)
- •§4. Практические приложения
- •Срочная доставка грузов
- •Использование уличных телефонных кабин
- •Тема 5. Замкнутые смо (циклические, сож при ограниченном входящем потоке)
- •§1. Модель замкнутой смо
- •§2. Пгр и стационарное решение (для замкнутой смо)
- •§3. Показатели эффективности замкнутых смо
- •§4. Оптимальное число линий в замкнутых смо (на примере расчета оптимального числа линий починки станков-автоматов)
- •§5. Практические приложения модели замкнутых смо
§ 3. Задание потока вызовов
Способ 1: Поток вызовов как случайный
процесс.
![]() .
.
![]() - число вызовов, поступивших в промежутке
- число вызовов, поступивших в промежутке
![]() .
.
![]()
![]()
Если меняется, то - семейство случайных величин, зависящих от - случайный процесс.
Свойства :
Дискретность:
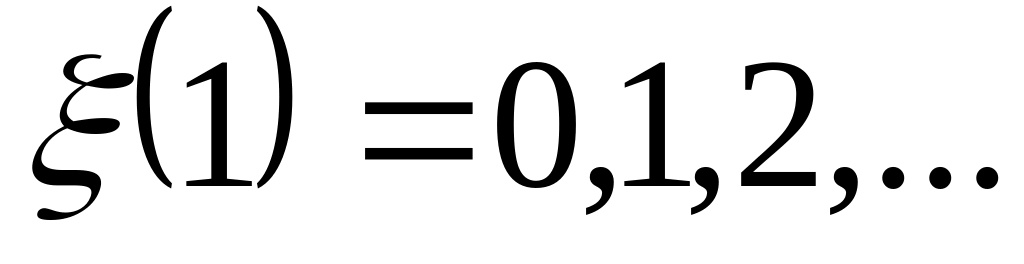
Монотонность реализации: количество вызовов не уменьшается с течением времени.
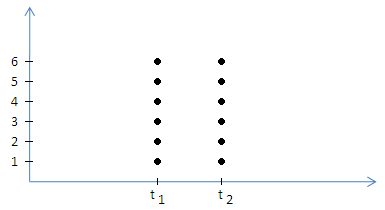
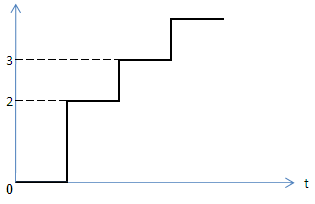
Необходимо знать функцию распределения вектора
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ,
где
,
где
![]() - произвольный набор целых неотрицательных
чисел.
- произвольный набор целых неотрицательных
чисел.
![]() ;
;
![]()

Способ 2:
![]() - начальный момент потока.
- начальный момент потока.
![]() - момент поступления
-го
вызова
- момент поступления
-го
вызова
![]()
Свойства :
- непрерывная случайная величина
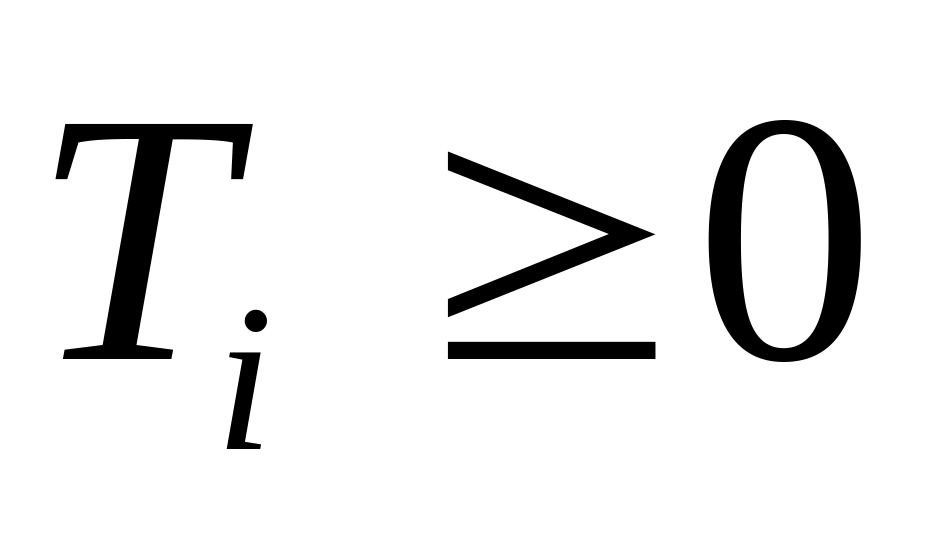
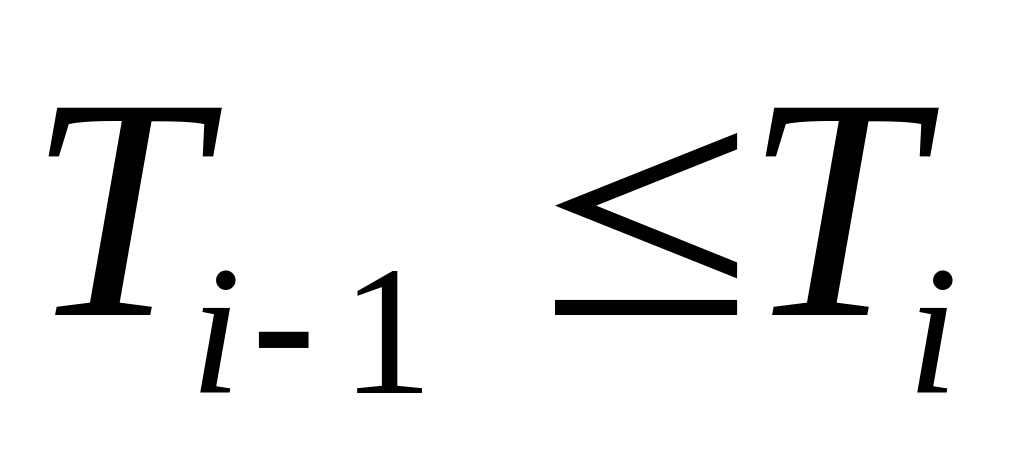 .
Возможно групповое поступление вызовов.
.
Возможно групповое поступление вызовов.
]![]() ;
.
;
.
![]() - длина промежутка времени между
- длина промежутка времени между
![]() и
.
и
.
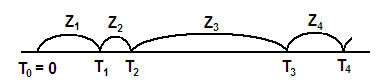
Свойства :
1. - непрерывная случайная величина.
2.
![]()
![]()
ОПР: Поток вызовов – последовательность
моментов их поступления.
![]() ,
образуется с помощью случайной величины
,
образуется с помощью случайной величины
![]()
![]() .
.
![]()
Поток задан, если известна
![]()
![]()
§ 4. Простейший поток вызовов
. Первое определение простейшего потока: поток вызовов простейший, если:
– марковский.
Вероятность поступления ровно вызовов в промежутке времени длиной не зависит от начального момента этого промежутка (условие стационарности).
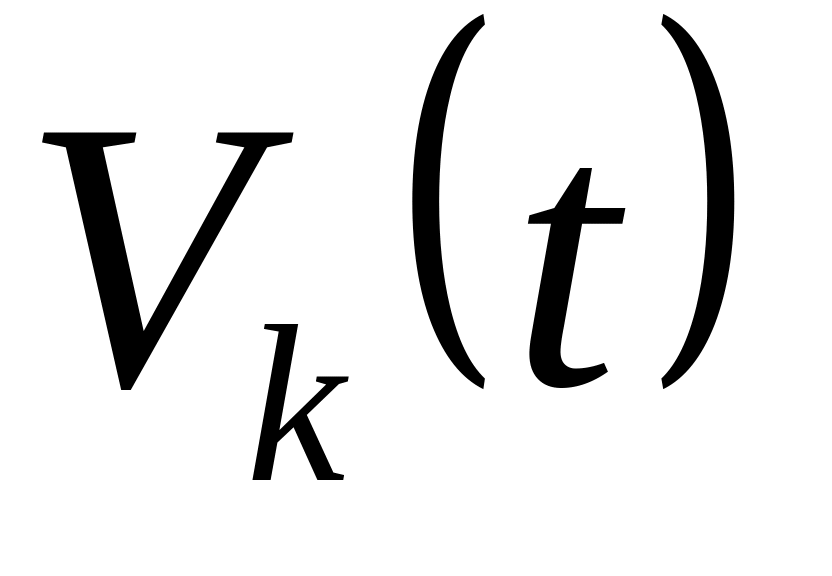
 ;
;
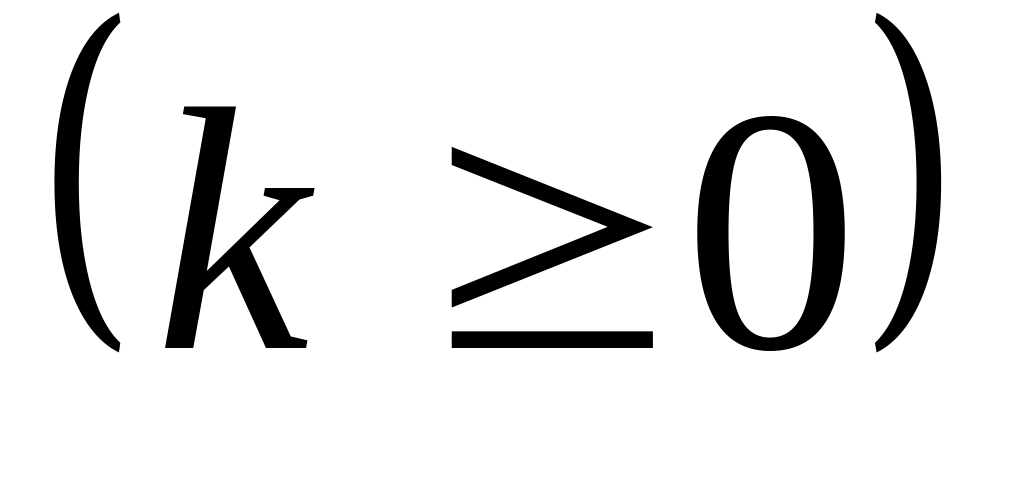 (1)
(1)
![]() ,
- параметр простейшего потока.
,
- параметр простейшего потока.
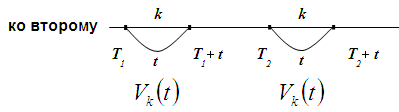
- кривая Пуассона -го порядка.
Графики
![]() ,
,
![]()
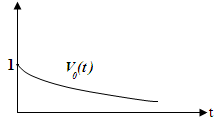
![]() ,
,
![]()
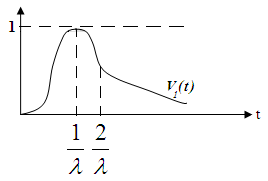
![]() ,
,
![]()
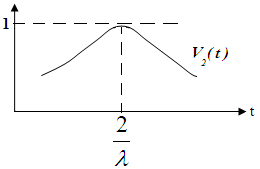
Два простейших потока могут отличаться друг от друга только значением параметра.
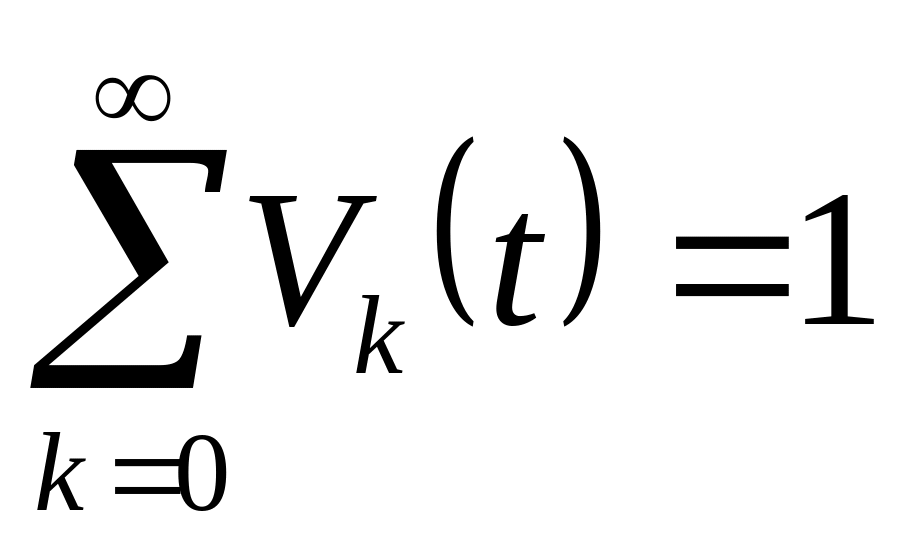
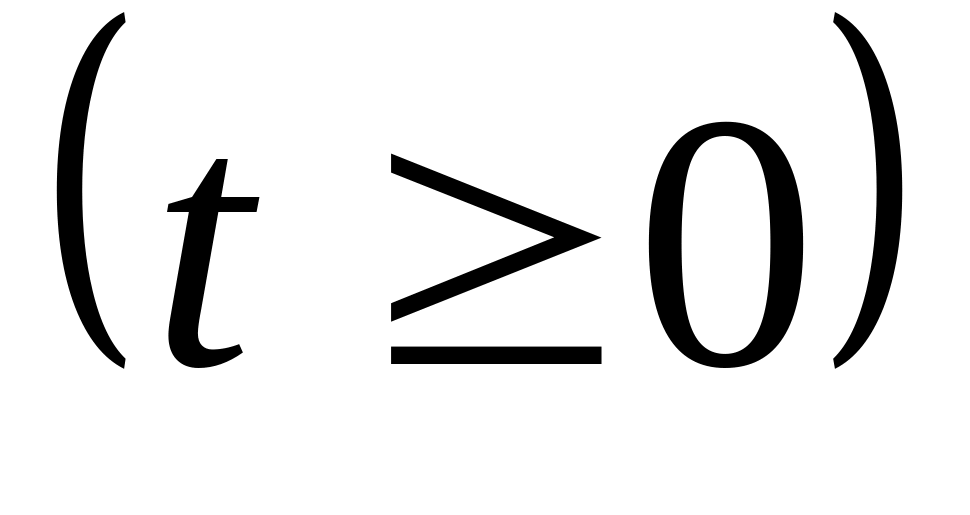
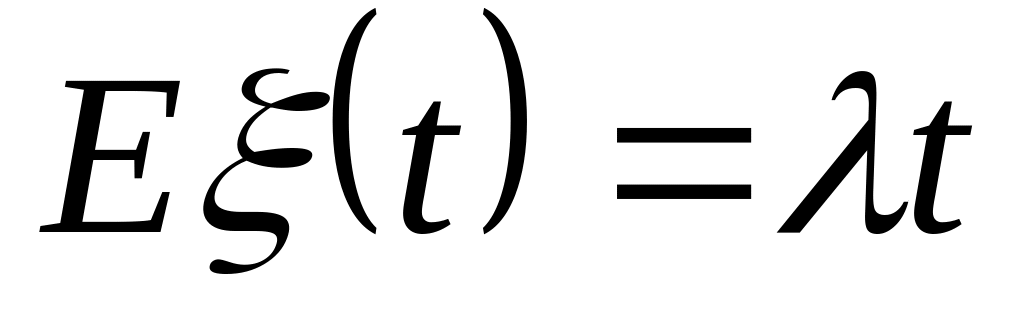
Академик Хинчин: простейшим является любой поток, который складывается из достаточно большого числа независимых источников вызовов.
Простейший поток есть ПГР:
![]() ,
,
![]() :
:
![]()
![]() ,
где
,
где
![]()
![]() с вероятностью 0.
с вероятностью 0.
![]() с вероятностью
с вероятностью
![]() ,
где
,
где
![]()
Примеры простейших потоков:
Поток вызовов на АТС.
Поток судов, прибывающих в данный порт.
Поток поломок (скажем, телевизоров).
![]() аргумент
- площадь.
аргумент
- площадь.
![]() аргумент
- объем.
аргумент
- объем.
ОПР:
![]() – интенсивность данного стационарного
потока – среднее число вызовов,
поступающих за промежуток единичной
длины
– интенсивность данного стационарного
потока – среднее число вызовов,
поступающих за промежуток единичной
длины
![]() .
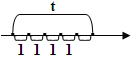
Среднее число вызовов в промежутке
пропорционально длине этого промежутка,
причем
является коэффициентом пропорциональности.
.
Среднее число вызовов в промежутке
пропорционально длине этого промежутка,
причем
является коэффициентом пропорциональности.
![]() ;
;
![]() ;
;
![]()
Для простейшего потока
![]() .
.
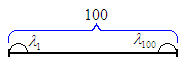
Расчёт (или ) на практике.
Пусть существует 100 промежутков единичной длины.
![]() - фактическое число вызовов.
- фактическое число вызовов.
![]()
Рассмотрим второе определение:
![]() поток вызовов называется простейшим,
если для него выполняется следующее:
поток вызовов называется простейшим,
если для него выполняется следующее:
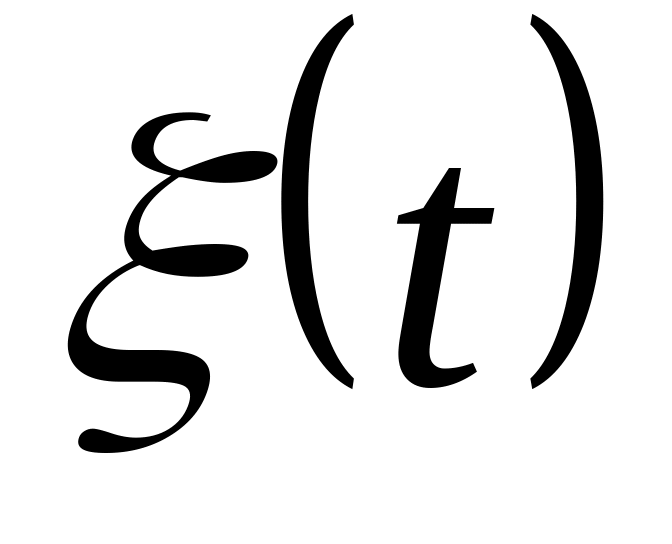 – марковский
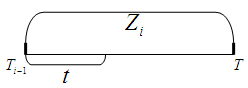
– марковский- независимые случайные величины
Все
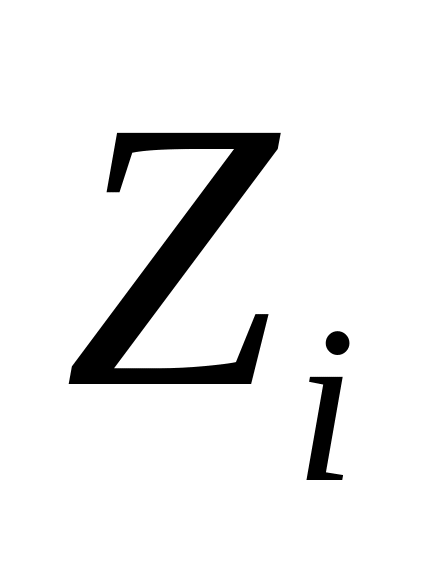 распределены по одному и тому же закону,
P
распределены по одному и тому же закону,
P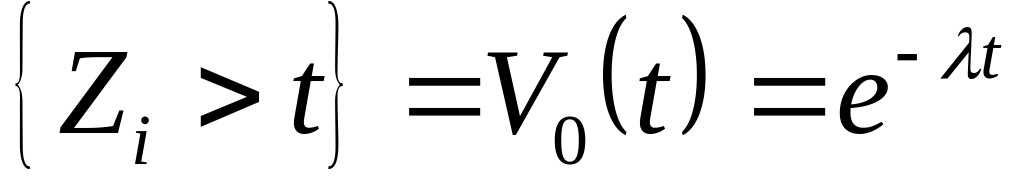 для
для
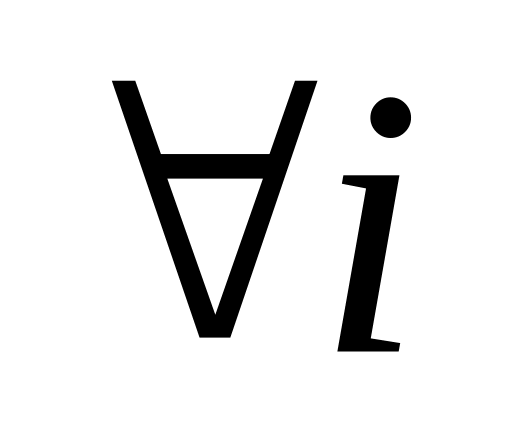 .
.
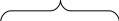 Определения эквивалентны.
Определения эквивалентны.
1
З
 амечание:
амечание:
![]() .
вызовов
.
вызовов

§ 5. Свойства показательного распределения разговора
- длина разговора.
![]()
![]() - вещественное число.
- вещественное число.
Пусть случайная величина
![]() - остаток разговора после момента
.
- остаток разговора после момента
.
![]() - функция распределения
.
- функция распределения
.
при
![]()
![]() - безусловная вероятность
- безусловная вероятность
при
![]() - условная вероятность.
- условная вероятность.
Теорема: Для того, чтобы был распределен так же, как и , необходимо и достаточно, чтобы закон распределения был показательным.
![]()
![]() (1)
(1)
Достаточность:
![]()
![]() .
.
![]() не зависит от
не зависит от
.
не зависит от
не зависит от
.
Необходимость - без доказательства.
Замечание 1: Если функции
распределения случайных величин
совпадают, то такие случайные величины
отождествляются.
![]() .
Тогда
- семейство случайных величин, зависящих
от
- случайный процесс.
.
Тогда
- семейство случайных величин, зависящих
от
- случайный процесс.
З амечание
2: Показательный закон играет
исключительную роль среди всех законов
распределения - только при показательном
законе распределения остаток ведет
себя так же, как и весь разговор.
амечание
2: Показательный закон играет
исключительную роль среди всех законов
распределения - только при показательном
законе распределения остаток ведет
себя так же, как и весь разговор.
![]()
в
вероятность закончиться у обоих
разговоров
![]()
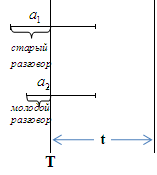
Замечание 3: Физический смысл показательного закона. Длина разговора является бесконечно малой величиной. Большинство вызовов нуждается в кратковременном (близком к 0) обслуживании. Поскольку в реальности дело обстоит не так, эта предпосылка неверна. Тем не менее, предполагаем закон распределения показательным.
Замечание 4: Со временем от
этой предпосылки удалось отказаться.
![]() - любое.
- любое.
Замечание 5: Физический смысл
параметра
:
![]() - средняя длина разговора.
- средняя длина разговора.
![]() - интенсивность обслуживания вызовов
на линии.
- интенсивность обслуживания вызовов
на линии.
Замечание 6: Расчет
.
Делаем 100 наблюдений за реальным временем
обслуживания
![]()
![]() .
.