Допущения в тмо:
линия в данный момент обслуживает не более одного вызова.
Каждый вызов обслуживается только одной линией.
начатый разговор не перебивается вплоть до его завершения.
СМО, где допускаются очереди, предполагает обслуживание порядке очереди.
Длины разговоров независимы от входящего потока и друг от друга.
Замечание: ]
- положительная непрерывная случайная
величина.
распределено по показательному закону,
если
имеет показательный вид:
(
).
- параметр показательного закона (темп
убывания функции).
.
.
- средняя длина разговора.
- интенсивность обслуживания вызовов
на линии.
- интенсивность обслуживания вызовов СМО. Групповое обслуживание – обслуживание вызова всеми линиями в пучке.
- время обслуживания вызова
-й
линией,
,
- распределение для
(или
).
Тогда
- продолжительность комплексной операции
по обслуживанию вызова. ]
все
для
.
Случай 1: Макрооперация завершена, когда закончится хотя бы одна элементарная операция.
;
;
;
;
Случай 2: Макрооперация завершена, когда закончатся все элементарные операции.
;
;
Тема 1. Основы тмо
§ 1. Понятие о случайном процессе и его марковости
]
- вещественное число:
.
]
- случайная величина при
фиксированном
.
Если
меняется, то
- случайный процесс – семейство случайных
величин, зависящих от
.
Случайный процесс считается заданным
(известным), если для
конечной группы значений
:
,
;
известен закон распределения вектора
.
В ТМО - состояние СМО.
:
0, 1, 2,…
,…
;
- дискретный случайный процесс
.
.
;
- целые, неотрицательные,
Возьмем
;
;
;
;
;
;
за
- марковский (без последействия), если
не зависит от состояний, в которых был
процесс до
.
;
§ 2. Понятие о процессах гибели и размножения (пгр). Стационарное решение и его интерпретация.
ОПР:
:
0, 1, 2,…
,…
;
- произвольный момент времени;
;
.
за
а)
с вероятностью
б)
с вероятностью
в)
с вероятностью
Если для случайного процесса выполняются эти условия, он называется ПГР.
-
параметры процесса, не зависящие от
прошлых состояний системы.
Вероятность перехода
за
равна
,
если
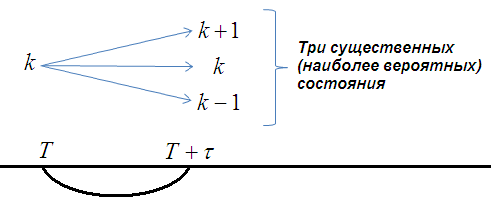
В биологии: состояние - численность популяции.
для
ПГР. Если
- это процесс размножения (ПР).
Если
,
то
.
Если
либо
(для случая
)
– это процесс гибели (ПГ).
Постановка задачи Эрланга для ПГР
Нахождение семейства функций
.
Семейства :
Неотрицательность:
(
;
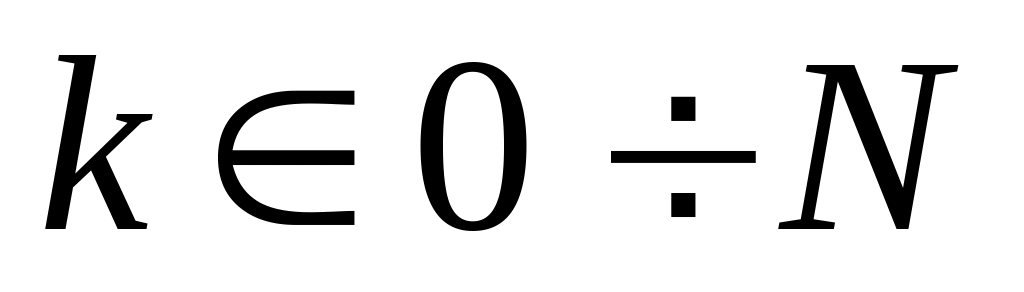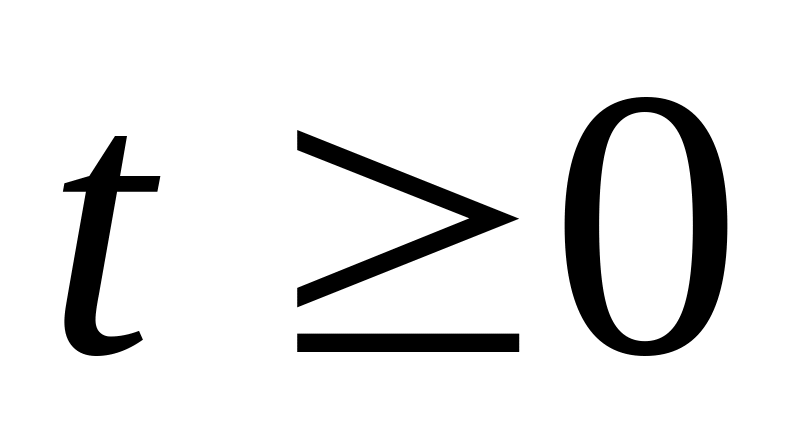)Вся совокупность этих функций удовлетворяет нормировочному условию:
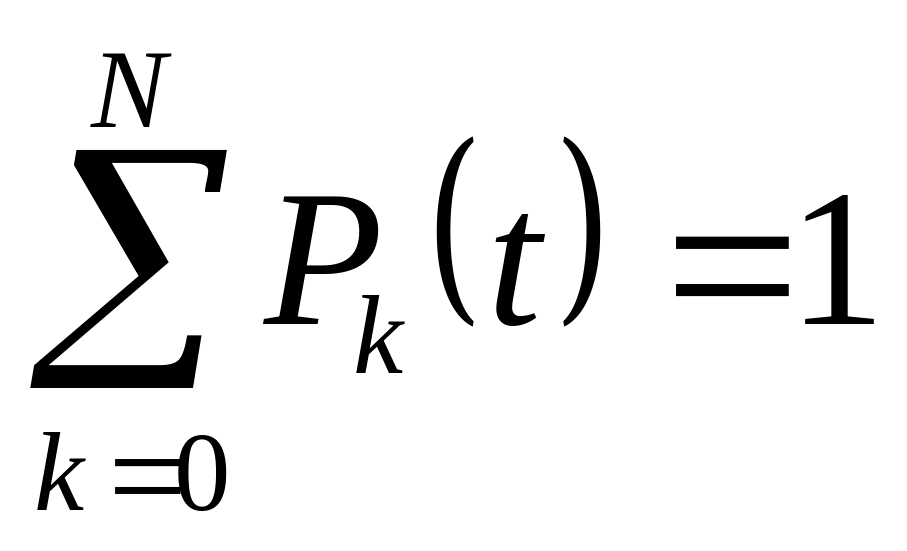
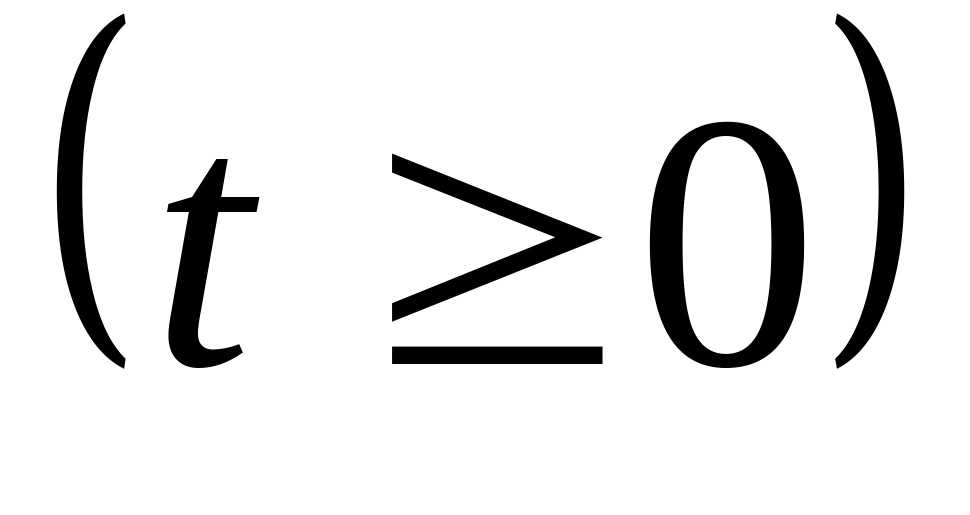
Если
,
- взрыв невозможен.
]
,
,
- начальные вероятности.
зависит от
.
;
:
,
;
при некоторых условиях.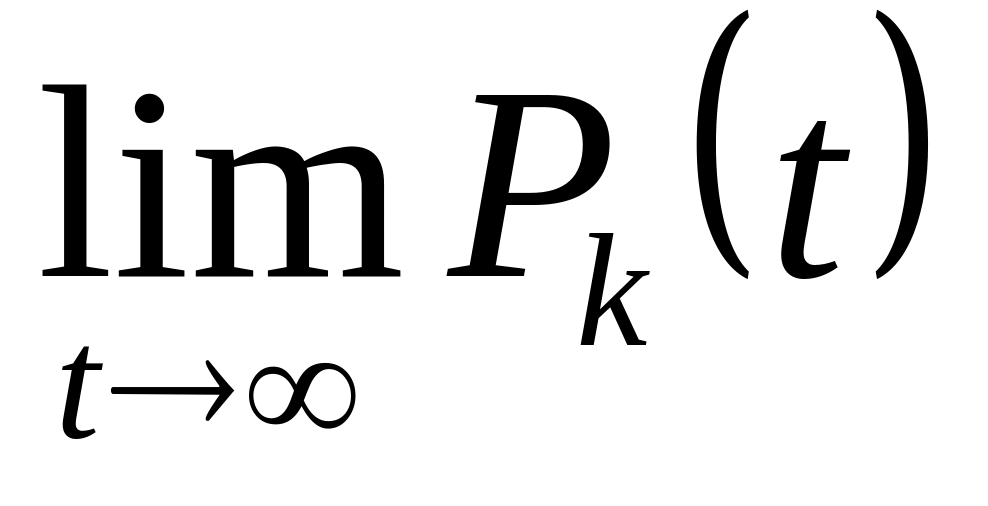
не зависят от
.
Нахождение
- задача Эрланга в предельной форме –
задача нахождения стационарного решения.
Свойства :
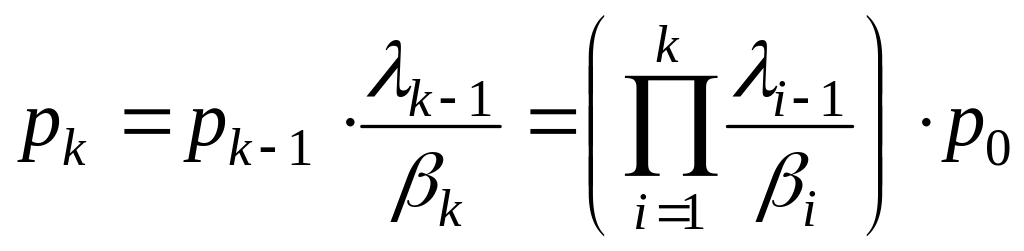
Замечание: если
,
] правое слагаемое меньше
,
если
.
.
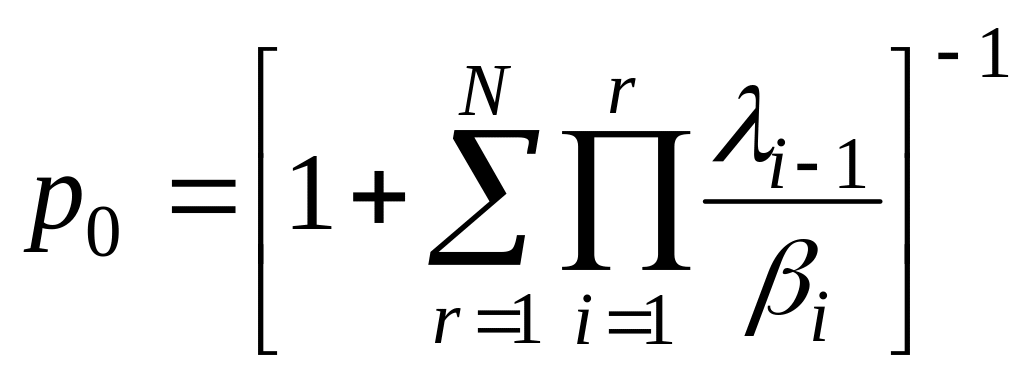Тогда
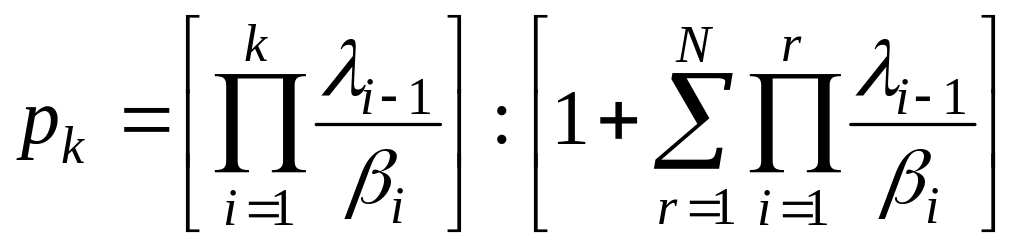
Интерпретация :
- вероятность
-го
состояния (ровно
вызовов в системе).
.
.
]
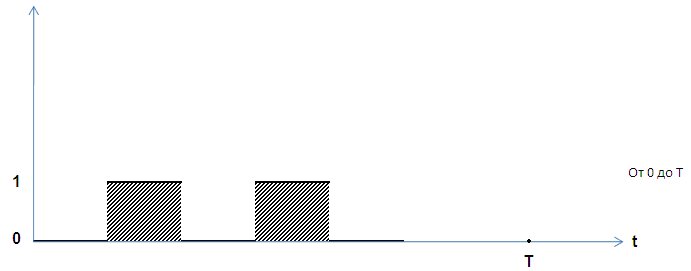
- время пребывания СМО в состоянии
-
среднее относительное время пребывания
СМО в состоянии
.
Теорема (эргодическая):
,
то есть
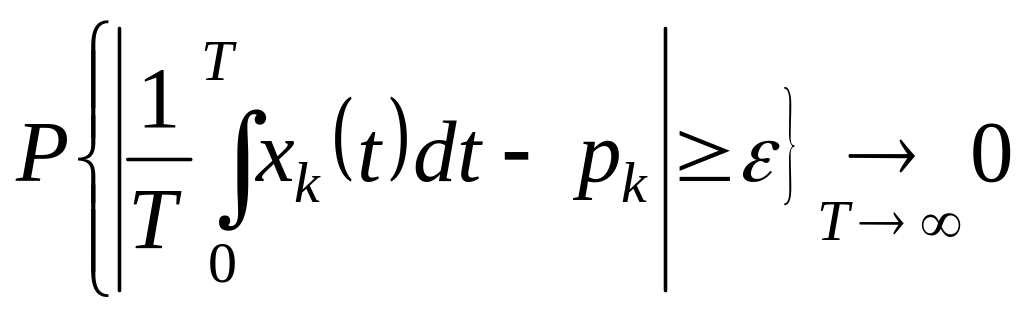
- среднее относительное время пребывания
процесса в состоянии
.
Если
– большое, то
- средняя длина промежутка времени, в
течение которого в системе было ровно
вызовов.