Области применения тмо

1. Экономика и организация производства.

2. Транспорт.

3. Техника.

4. Военное дело.

5. Естествознание (ядерная физика, биология).

§ 2. Необходимость вероятностного моделирования (на примере расчета числа причалов в порту).

Подходы:

1. Вероятностный.

2. Детерминированный – применяется при отсутствии статистики.

] – годовой план обработки грузов в порту (в тоннах).

] – средняя грузоподъемность судна (в тоннах/судно).

] – пропускная способность одного причала (интенсивность обработки вызовов на линии) (в судах в сутки).

.

] – эффективный фонд времени работы порта в течение года (в сутках).

Ежесуточно в порт должны прибывать в среднем судов. - интенсивность прибытия судов в порт. - пропускная способность порта с причалами.

; (1)

] (округление до большего натурального). Тогда .

(1) предполагает, что все причалы загружены непрерывно Либо суда прибывают в порт в моменты освобождения причалов, либо в порту всегда есть очередь судов, ожидающих обработки. Первое на практике не выполняется, поскольку:

1. в графике работы порта предусматривается не конкретная дата прибытия судна в порт, а интервал значительной длины момент прибытия судна – случайная величина.

2. время обработки судна колеблется в широком диапазоне оно тоже является случайной величиной в порту всегда есть очередь достаточной длины.

§ 3. Основные понятия и допущения.

СМО – организация, которая может выполнять работу (предоставлять услугу) одного вида.

Вызов (требование) – заявка на выполнение работы (предоставление услуги), на которую способна данная СМО.

Поток – входящий и выходящий.

Входящий поток. Примеры:

1. поток вызовов на АТС.

2. поток судов, прибывших в данный порт.

3. поток сломанных объектов (неисправных а/м, телевизоров).

Для СМО с ожиданием (СОЖ) входящий поток распадается на поток немедленно обслуживаемых вызовов и поток вызовов, попадающих в очередь.

Выходящий поток вызовов – вызовы, покидающие данную СМО. Для систем, где существуют отказы, выходящий поток распадается на поток обслуженных вызовов и поток вызовов, получивших отказ.

Состояние СМО – количество вызовов, имеющихся в СМО на тот или иной момент времени . ;

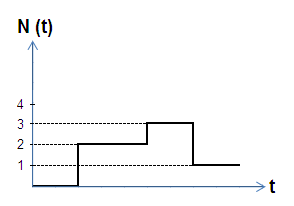
Линия – обслуживающий прибор. Иногда реальных линий может и не быть, и их можно ввести идеально.

Пучок линий – совокупность всех линий в СМО. Он конечный, если ( – количество линий в пучке), бесконечный в противном случае.

Пучок линий полнодоступен, если его линия может обслуживать поступающий вызов, и поступающий вызов согласен быть обслужен линией.

Пучок линий упорядочен, если все линии пронумерованы, и вызов занимает линию с наименьшим номером из числа свободных линий.

Разговор – – время обслуживания на линии. – непрерывная случайная величина, , её функция распределения считается известной.

] . Тогда свойства таковы:

1. не возрастает.

2. , .

3. , .

4. .

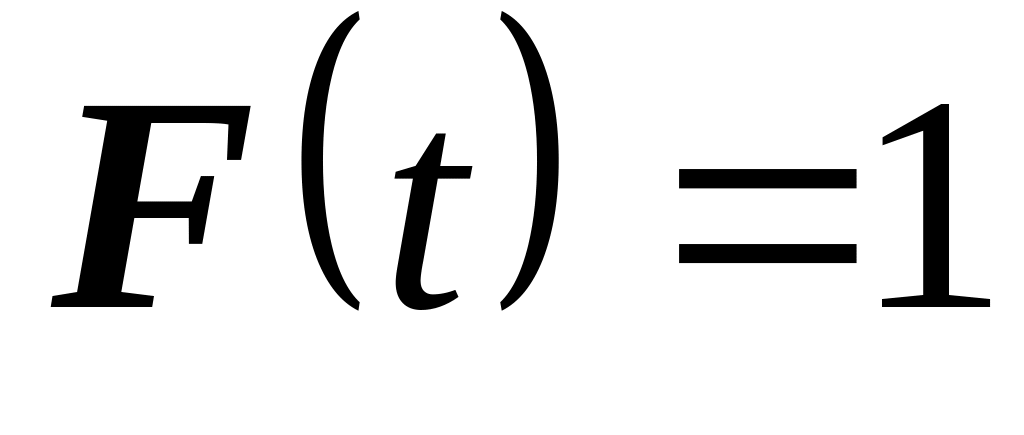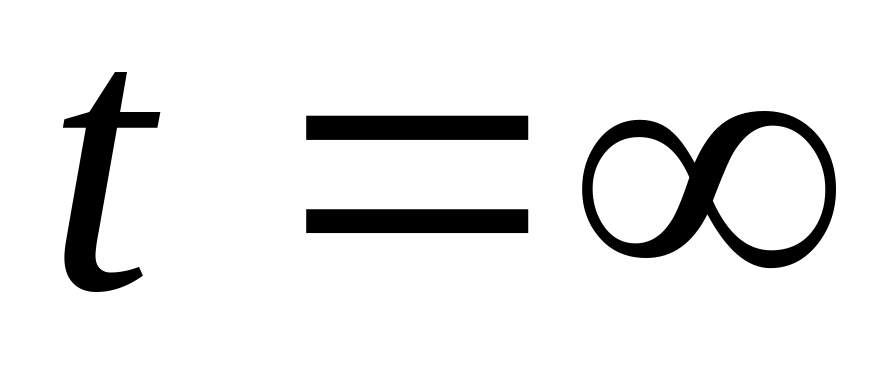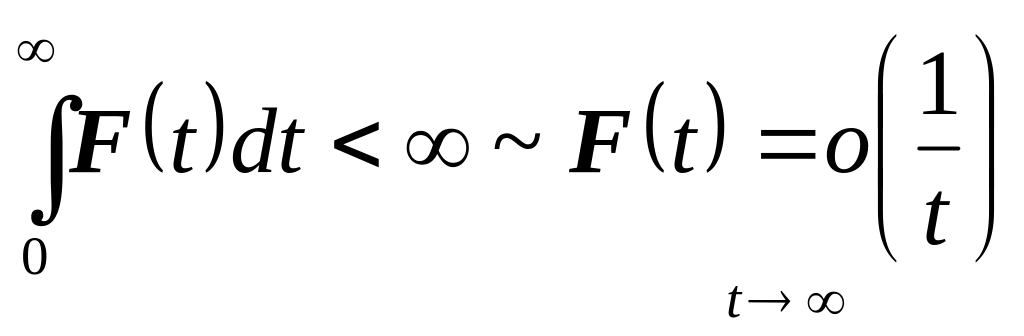, где , поскольку .