§4. Оптимальное число линий в замкнутых смо (на примере расчета оптимального числа линий починки станков-автоматов)
I. Пусть – количество линий.
Пусть – количество станков-автоматов (СА).
Пусть
– время исправной работы одного СА.
.
Обслуживание - наладка.
– время наладки
II. Пусть существует 2
наладчика и
станков. Возможны две формы организации
обслуживания.
Индивидуальная форма многостаночного обслуживания: за каждым из рабочих закрепляются свои
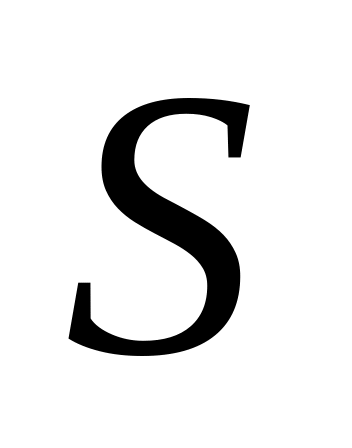СА.
,
для обеих СМО.
Агрегатная форма многостаночного обслуживания.
,
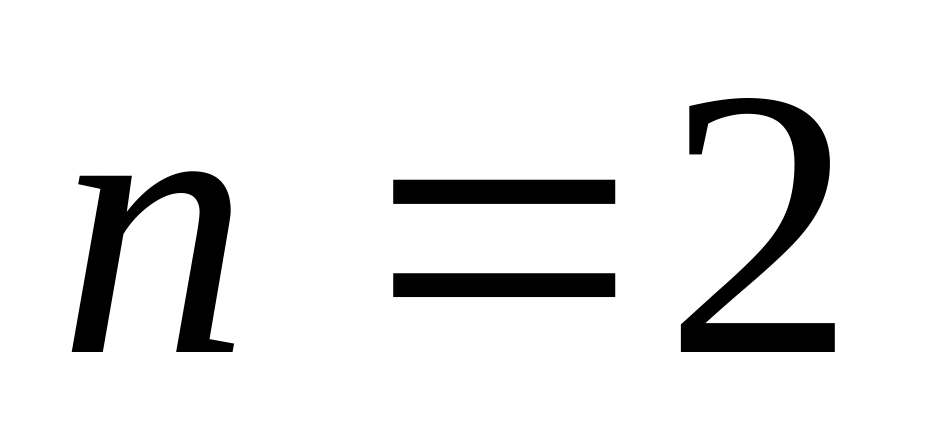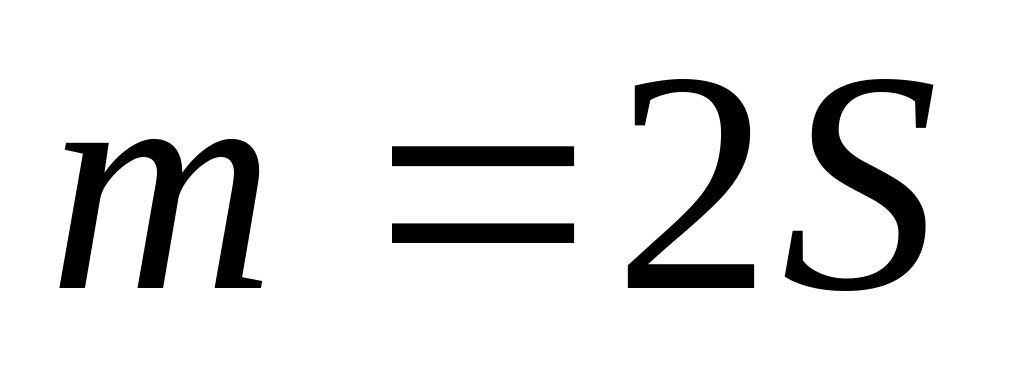
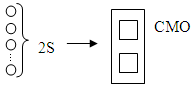
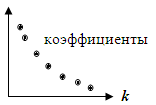
Критерии:
,
,
Агрегатная форма лучше. целесообразно создавать бригаду и поручать ей все станки.
III.
.
Постановка задачи.
– фиксировано.
.
.
|
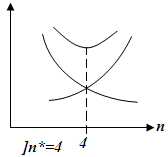
Плохо иметь слишком много – будут простои, плохо иметь слишком мало – будут простои СА. |
.
Критерий
оптимальности – суммарные средние
издержки из-за простоя обоих видов -
.
.
,
– издержки из-за простоя в единицу
времени
1 – наладчиков (зарплата наладчикам идет).
2 – станка (продукция не производится).
§5. Практические приложения модели замкнутых смо
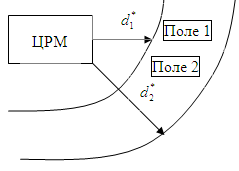
I. Выбор централизованного или местного ремонта однотипных сельскохозяйственных машин (СХМ). Центральная ремонтная мастерская – ЦРМ.
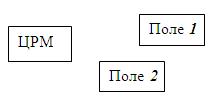
– время исправной работы всех (каждой)
СХМ,
показательно распределено,
.
ЦРМ может выслать бригаду в поле для
ремонта (местный ремонт); ремонт может
быть осуществлен в ЦРМ.
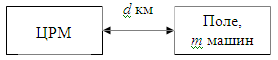
Допущения:
а) Для обоих видов ремонта:
– время ремонта, распределено .
б) Для ЦРМ
1)
- скорость доставки сломанной машины,
км/ч.
2) Мощность мастерской настолько велика, что к ремонту любой доставленной СХМ она может приступить немедленно.
в) Для МРМ
1) При ремонте СХМ возможно стояние её в очереди.
2)
;
1) при
целесообразно.
- время доставки ЦРМ
- время стояния в очереди.
,
Пусть
;
;
;
?
.
;
.
Два поля:
,
.
Для обоих полей вычисляем
,
.
II. Ремонт кораблей в доках.
кораблей;
дока. Пусть
года
месяцев.
- случайная величина.
.
Пусть - 2 месяца (средн.)
-
.
(сч. в месяцах),
.
Среднее число простаивающих кораблей.
;
Район защищён, если в строю находится не менее восьми кораблей.
Среднее количество кораблей, ожидающих ремонта.
.
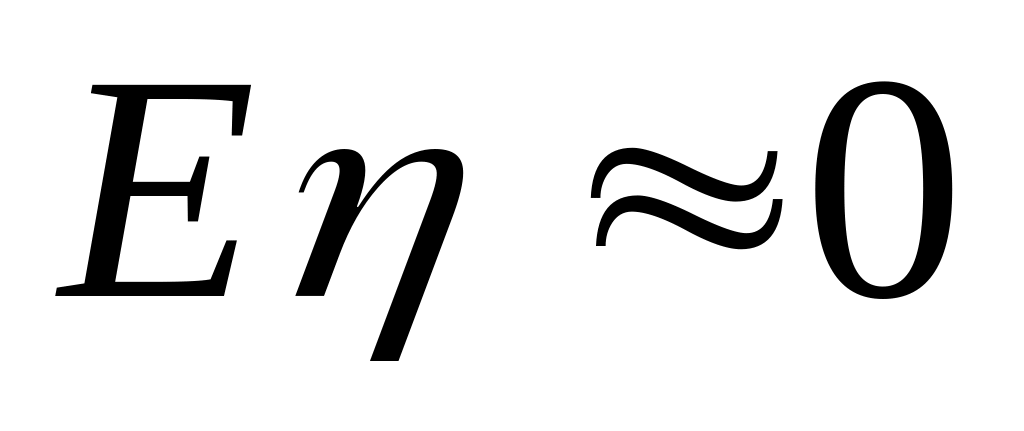