Тема 5. Замкнутые смо (циклические, сож при ограниченном входящем потоке)

§1. Модель замкнутой смо

I. Пусть – количество станков в группе станков. Станки выполняют одинаковые операции. – количество обслуживаемых объектов.

Пусть . ( – не интересный случай, так как часть станков постоянно простаивает).

- время исправной работы объекта.

- непрерывная случайная величина, распределенная по показательному закону с параметром . . В течение исправной работы объект находится вне СМО.

- среднее время исправной работы объекта (нахождения его вне СМО). В момент поломки объект поступает в СМО. Если в этот момент существует свободная линия, объект занимает ее. Если все линии оказываются заняты – объект становится в очередь и находится в ней в течение времени . – неотрицательная непрерывная случайная величина.

- время обслуживания объекта (его ремонта). - положительная непрерывная случайная величина, распределенная по показательному закону с параметром . По окончании ремонта объект покидает СМО, и в дальнейшем снова становится источником поступления вызова.

II. Названия СМО.

Замкнутые СМО: в рассматриваемой ситуации входящий поток вызовов формируется из выходящего.

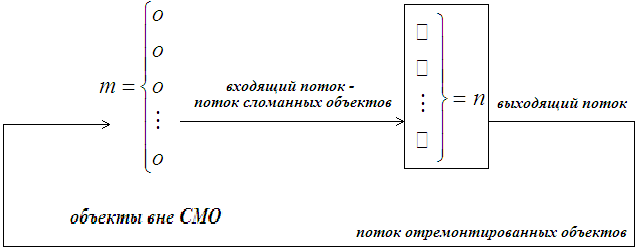
Циклические СМО: для любого объекта существует следующий цикл:

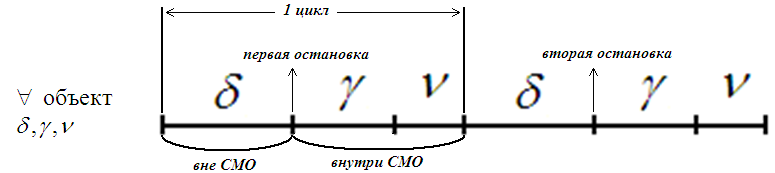СОЖ: отказов нет, однако входной поток ограничен ( « » объектов в СМО - значит, все объекты сломаны).

III. Состояния СМО.

- состояние.

означает:

а) - в СМО находятся ровно сломанных объектов (занято линий пучка).

б) - заняты все линий и объектов стоят в очереди.

Если объектов исправны и находятся вне СМО.

Поломки объектов не зависят друг от друга.

§2. Пгр и стационарное решение (для замкнутой смо)

а) ПГР

Утверждение: в случае замкнутой СМО - ПГР с параметрами ; ; ; .

! – не марковский в силу того, что входящий поток не является простейшим. Он является стационарным с последействием - примитивным потоком, следовательно, переходные вероятности не существуют. -е зависят от впервые.

Доказательство: ◄ Рассмотрим переходы:

1. Из « » в « » за : Для расчета вероятностей перехода будем пользоваться биномиальной вероятностью.

.

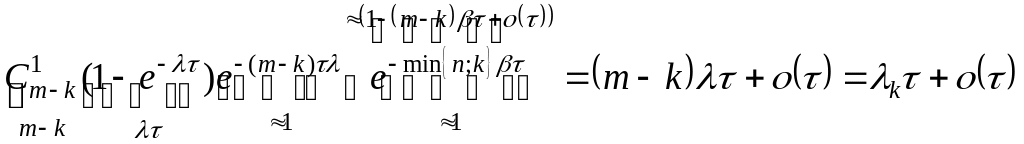
Линейная часть

2. за :

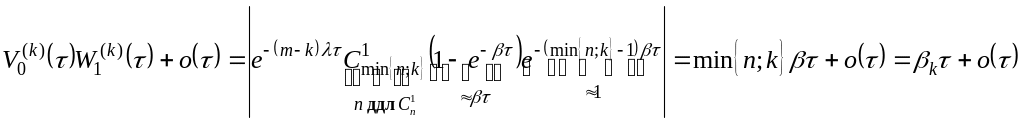
3.

б) Стационарное решение

(*)

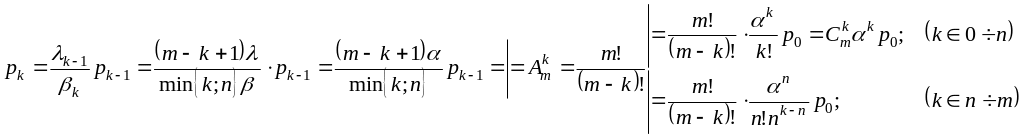
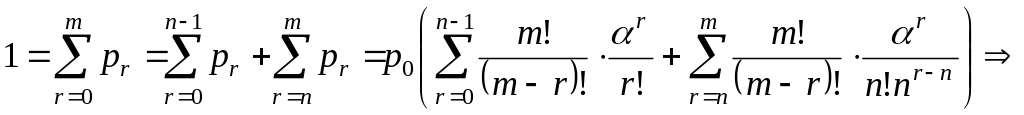
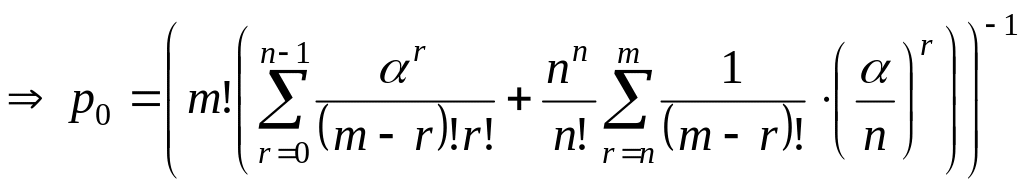
§3. Показатели эффективности замкнутых смо

1. Вероятность того, что вызову придется стоять в очереди.

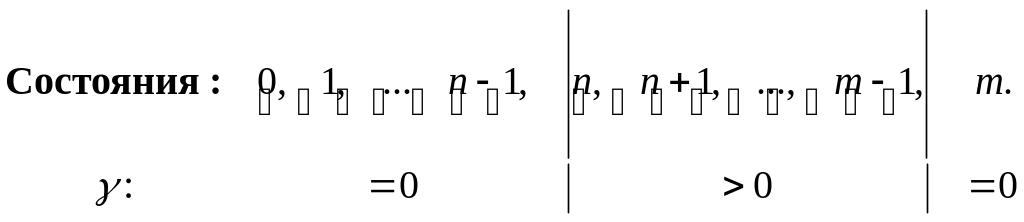
2. Вероятность полной загрузки

3. , , , - выбираем в качестве базового - среднее число вызовов в СМО.

.

а) Среднее число объектов вне (обслуживания в) СМО

б) Коэффициент простоя объекта в СМО

= [суммарное время простоя объектов в СМО за ]:[суммарный фонд времени объектов за ] =

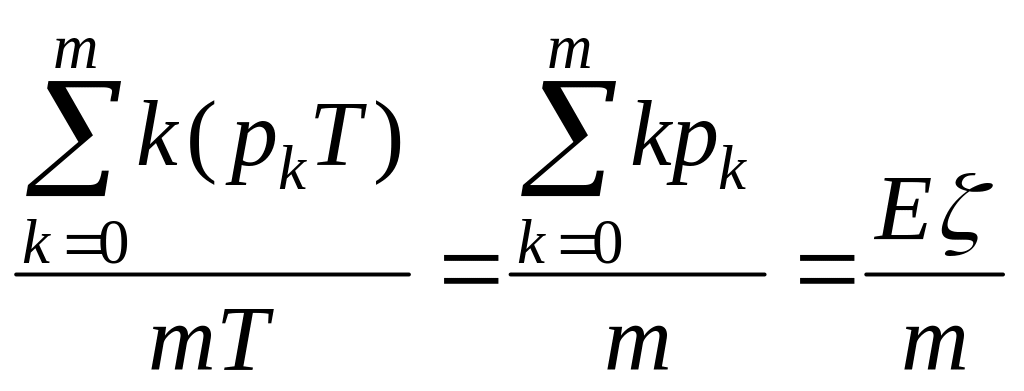
4. Среднее число занятых линий.

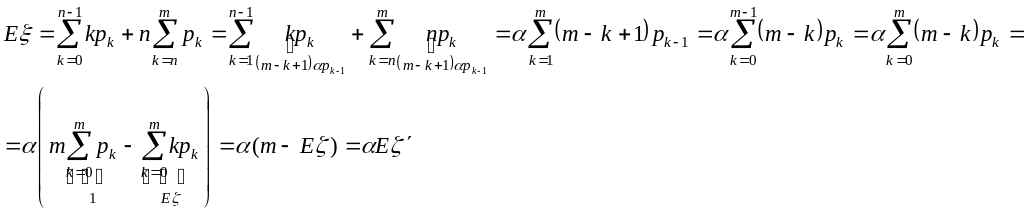Смежные показатели.

а) Среднее число свободных линий.

б) Коэффициент простоя линий

[Коэффициент загрузки] =

5. Средняя длина очереди. . Смежный показатель - коэффициент простоя объекта в очереди. = [суммарное время простоя объектов в очереди за ] : [Суммарный фонд времени объектов за ] =

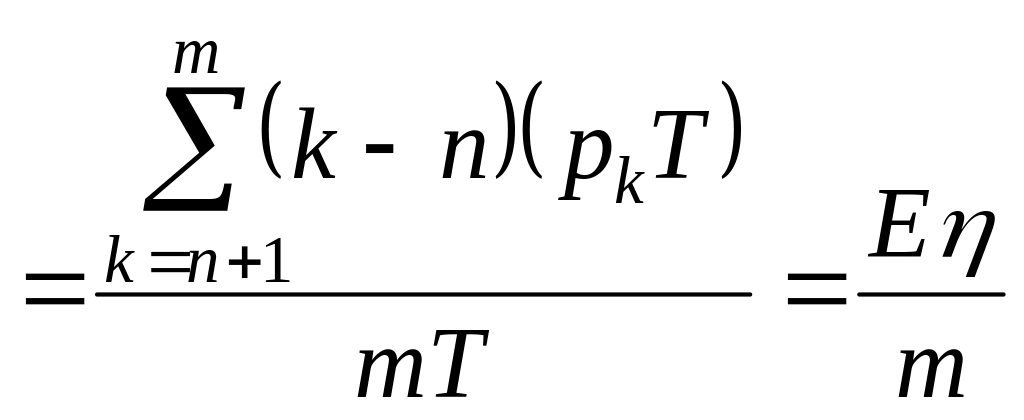
	Через какой показатель
Какой показатель