§3. Оптимальное число линий в соч (на примере расчета оптимального размера максимального запаса товара при задалживании спроса)
СМО – магазин.
Входящий поток – поток покупателей.
Допущения и исходные данные:
Поток покупателей – простейший с параметром :
;
;
.
В одни руки отпускается только одна единица товара (спрос Пуассоновский).
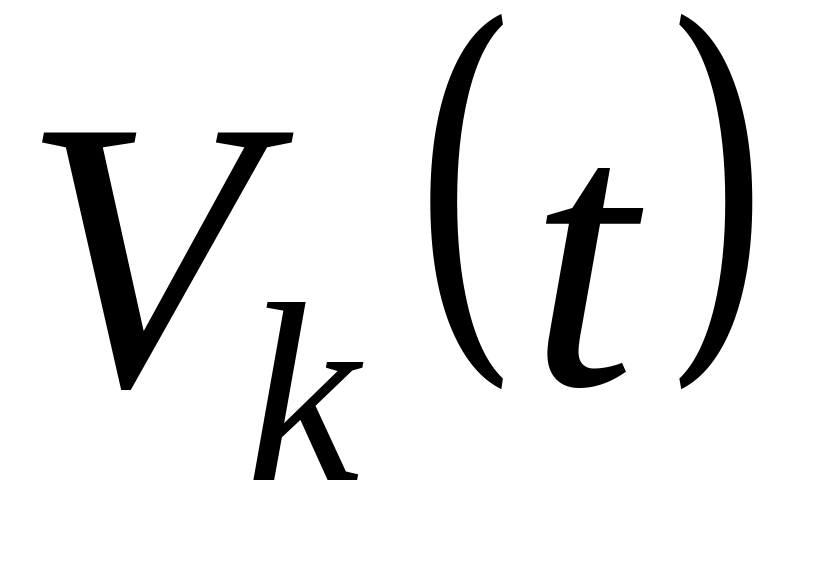.Как только происходит продажа товара, сразу же происходит заказ на ее замену другой единицей. Следовательно, число, равное сумме размера запаса товара и количества поданных заявок, является константой на любой момент времени.
- время выполнения заказа на пополнение запаса. Распределено по показательному закону - .
При отсутствии товара в магазине спрос задалживается, но не более чем для покупателей.
Пусть - доход от продажи единицы товара за вычетом издержек выполнения заказа на его доставку.
- среднее время выполнения заказа. Пусть - издержки хранения единицы товара за времени. Пусть - средняя прибыль магазина за .
.
- либо максимальный размер запаса
товара в магазине, либо максимальное
число поданных заявок.
Для решения можно воспользоваться моделью СОЧ.
Линия – ячейка. - количество линий.
Линия занята/свободна ~ ячейка пуста/заполнена. Обслуживание – выполнение заказа на заполнение пустой ячейки. Время обслуживания распределено показательно.
Состояние СО -
- количество поданных заказов.
Если , то:
а)
при
- подано «
»
заявок. Следовательно, размер запаса
товара равен
.
б)
при
- подано «
»
заявок и имеется очередь из
покупателей.
- средняя прибыль за
;
- средний доход за
;
- средние издержки за
.
,
где
- доходы;
- издержки.
а) Доходы приносят реализованные единицы
товара. Среднее число реализованных
единиц товара за
-
.
б) Издержки
.
Тогда
§4. Практические приложения
Срочная доставка грузов
СМО – АТК, принимающая заказы на доставку грузов.
Обслуживание – доставка груза. Так как доставка должна быть срочной, объем заявок ограничен величиной .
- количество автомашин в гараже.
Поток заявок – простейший с параметром .
- показательно распределенная случайная величина с параметром .
Числовые данные:
а/м;
.
Пусть
.
1.
Найти вероятность того, что все машины
находятся в гараже.
.
.
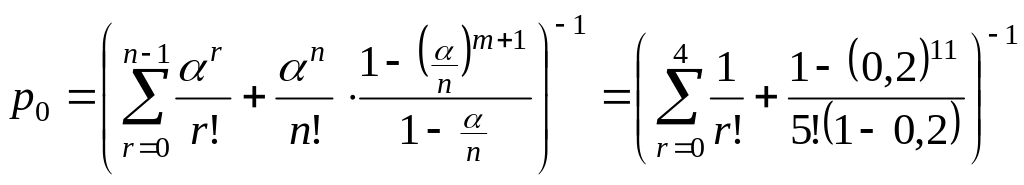Пусть
.
2. Найти вероятность того, что в СМО
подано ровно
заявок.
3. Вероятность того, что все линии заняты.
.
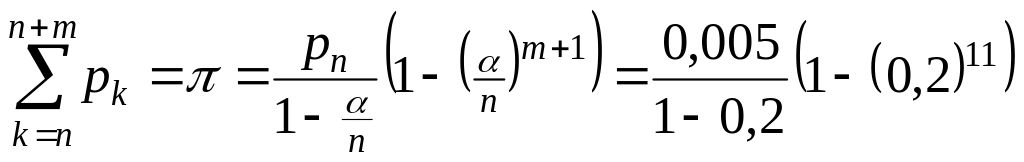Пусть
.
4. Средняя длина очереди заявок
.
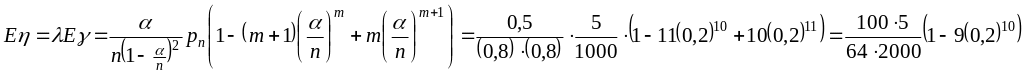Пусть
.
Использование уличных телефонных кабин
Пусть существует
соседних телефонных кабин. Пусть
.
Пусть
.
Поток желающих позвонить – простейший.
.
Время в кабине – случайная величина,
распределенная по показательному
закону с параметром
.
.
.
Найти среднюю долю времени, в течение которого:
а) пустовали обе кабины.
б) пустовала только одна кабина.
Вероятность того, что желающему позвонить придется искать другую кабину.
Найти среднее время ожидания разговора.
