Тема 4. Системы с ограниченной очередью
§ 1. Модель, пгр, стационарное решение и распределение времени ожидания для систем с ограниченной очередью
Модель. Исходные данные те же самые
Входящий поток – простейший с параметром . - количество линий, - максимально допустимый размер очереди.
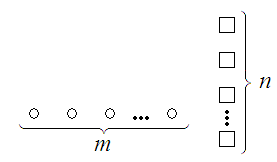
Если в момент поступления вызова существует свободная линия – вызов приступает к разговору. Если все линии заняты, то
а) вызов остается в СМО, если длина
очереди
;
б) вызов получает отказ, если длина
очереди
.
Пример – система с ограниченным числом мест ожидания (зал ожидания).
Система с ограниченной очередью (СОЧ) относится к классу смешанных СМО (есть и время обслуживания, и время ожидания)
Состояние СМО.
Всего
состояний.
означает, что:
а)
-
линий заняты (
вызовов на обслуживании),
свободны.
б)
- заняты все
линий (
вызовов на обслуживании) и имеется
очередь
.
ПГР.
Утверждение: в случае СОЧ случайный
процесс
является марковским ПГР с параметрами
;
Доказательство: ◄ То же, что и для СОЖ.
– марковский по Теореме (входящий поток простейший, а время обслуживания распределено по показательному закону).
– ПГР
а)
б)
в)
Стационарное решение:
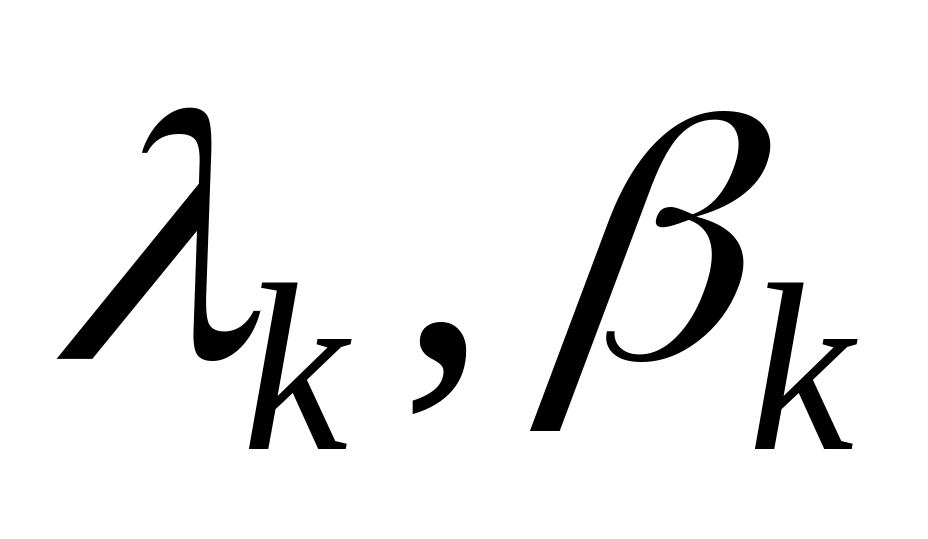- такие же, что и для СОЖ
выражение
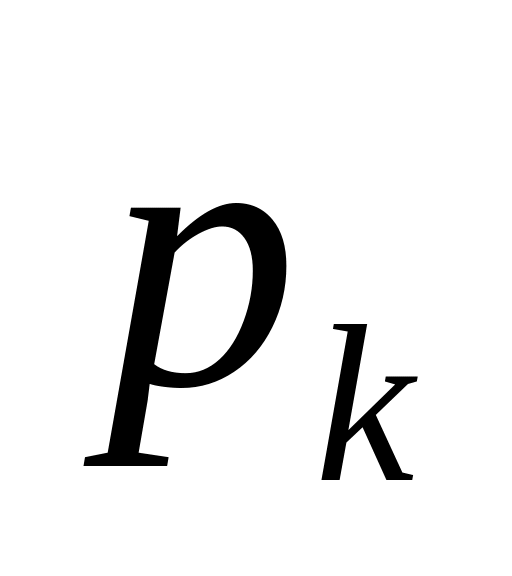через
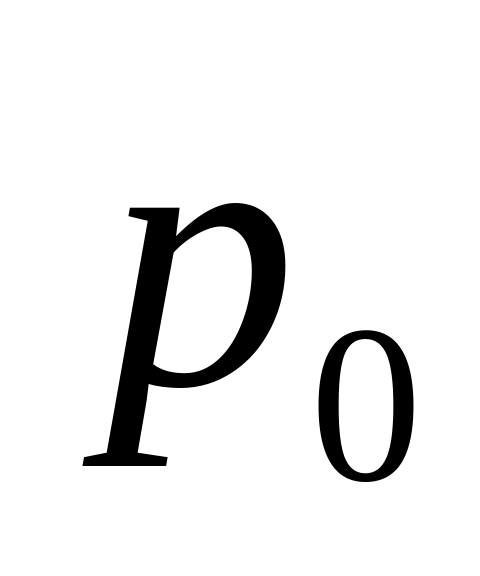таково:
(**)
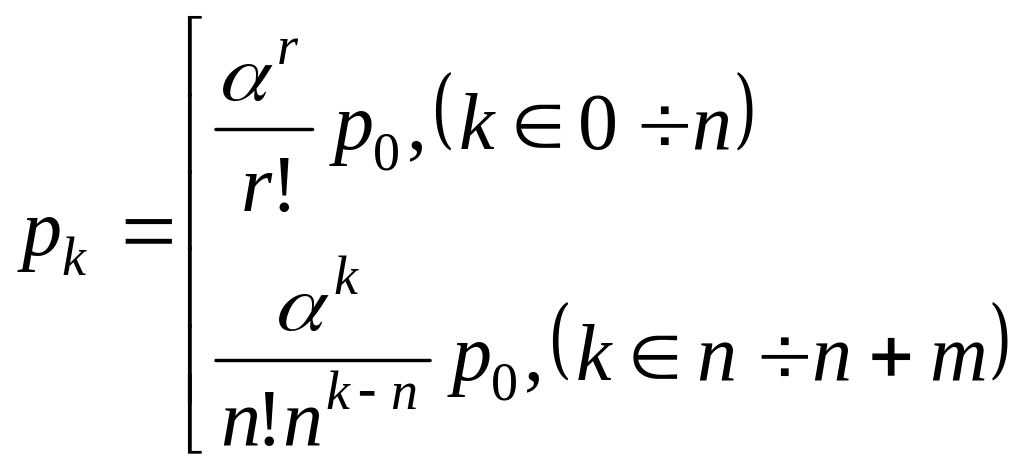- другое. - ?
Ряд конечен и нет проблем со сходимостью
{
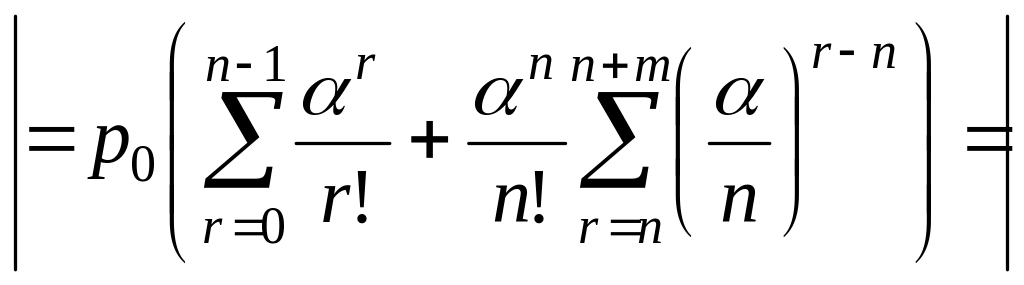- первый член прогрессии,
- знаменатель.
}
Конечная геометрическая прогрессия,
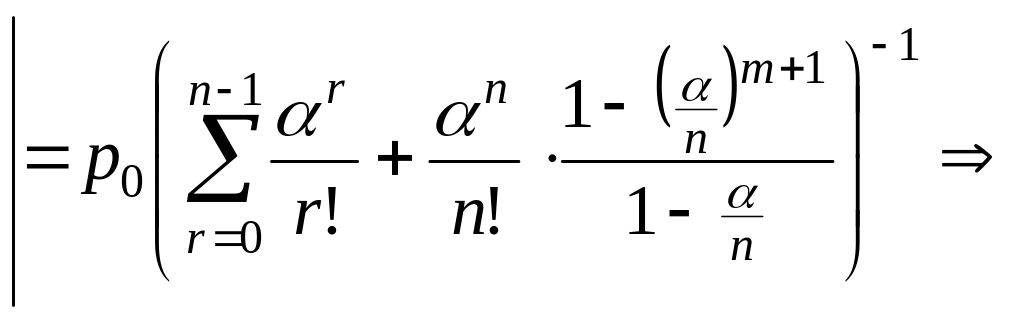подставляя
в (**), получаем
.
(
– число слагаемых).
Распределение времени ожидания.
Сохраняем обозначения и рассуждаем в
случае СОЖ
получим:
;
для
есть свободная линия и для
причем
- поток освобождений (простейший).
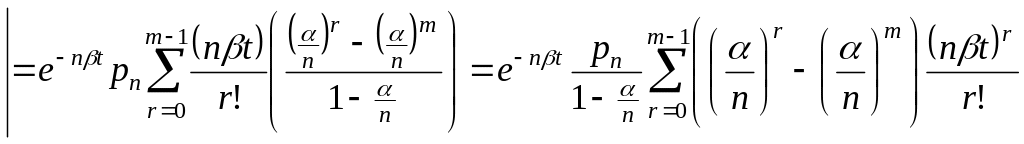
так как
– сумма геометрической прогрессии.
При этом
- длина очереди освобождений линий.
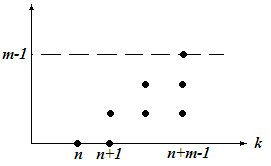
§2. Показатели эффективности соч
Вероятность отказа
.
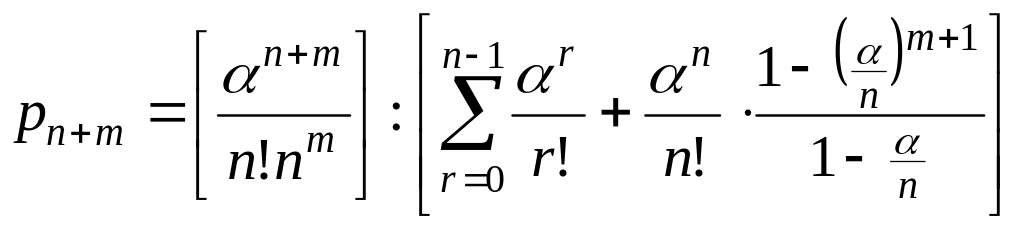Вероятность того, что вызов будет
обслужен
- коэффициент обслуживания (средняя
доля обслуженных).
2 исхода
Потоки отказов и обслуженных вызовов
являются простейшими с параметрами
и
соответственно (из свойства расщепления
простейшего потока).
Среднее число занятых линий.
- число занятых линий.
Состояния СО: 0, 1, … 
: 0, 1, …
Вероятности:
,
,
… 
,
.
При
- СОТ
;
;
Замечание:
.
а)
= [интенсивность обслуженных вызовов
]:[интенсивность
обслуживания на любой линии
].
б)
= [среднее число обслуженных за единицу
времени]
= [среднее число обслуженных вызовов
за
]
Способ 1: (используя стационарное решение - )
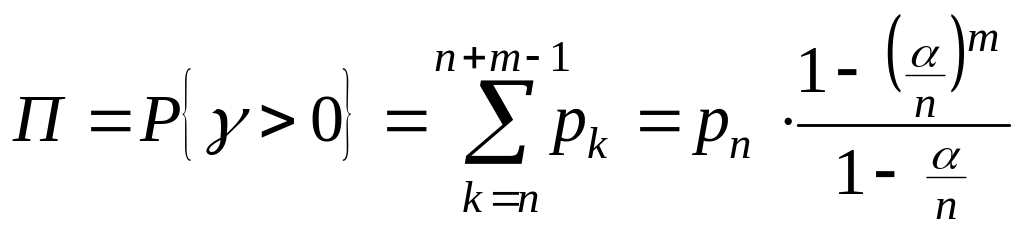
Способ 2: (используя функцию распределения)
;
.
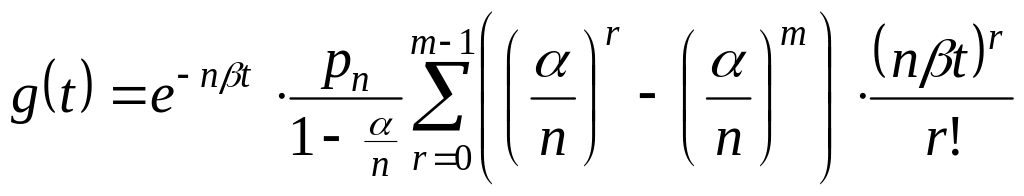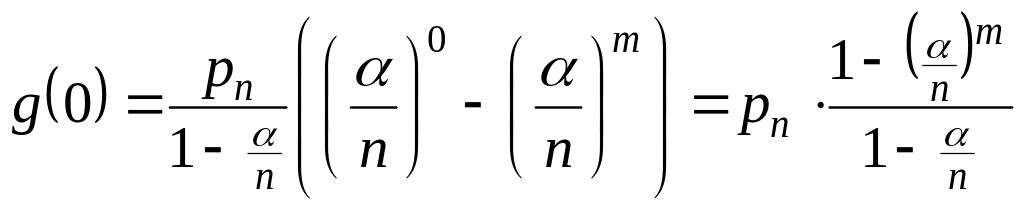Замечания:
а)
- СОТ.
б)
;
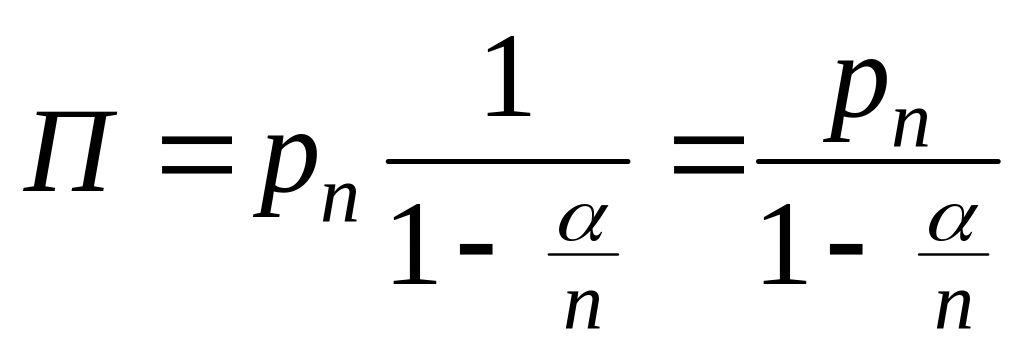для СОЖ.
Вероятность полной загрузки (вероятность того, что заняты все линии).
Пусть
- полная загрузка.
геометрическая прогрессия
.
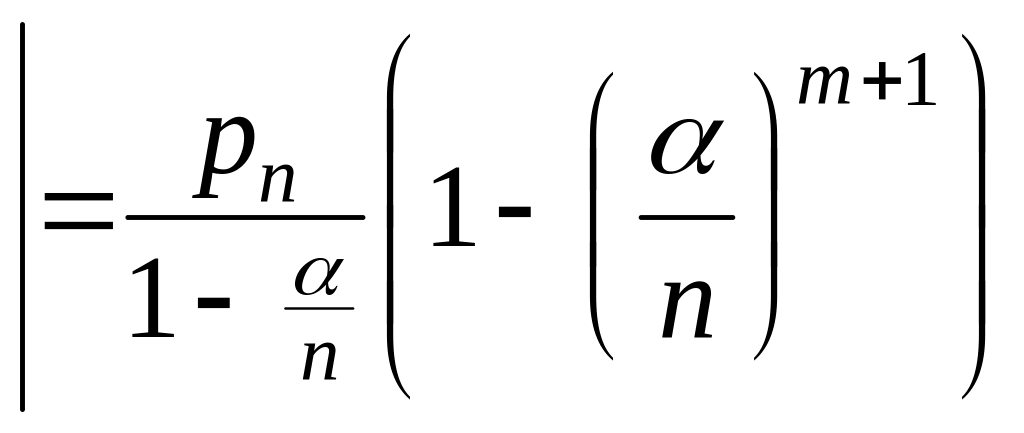Смежный показатель – вероятность того, что существует свободная линия (вероятность немедленного обслуживания).
Среднее время ожидания обслуживания.
- не надо
в соответствии с площадью под кривой
Пуассона
Среднее время пребывания вызова в СМО
Средняя длина очереди:
,
поскольку
Среднее число вызовов в СО
