Оптимальная интенсивность пополнения запаса товаров в магазине.
Входящий поток – поток покупателей. Кроме того, существует и поток товаров.
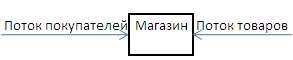
Обслуживание – обеспечение покупателя
товаром. В такой СОЖ за любой конечный
промежуток
может поступить любое количество
покупателей.
- вероятность того, что за время
поступит
вызовов. В СОЖ каждый вызов обязательно
должен быть обслужен.
Задача некорректна, поскольку поток товаров конечен, а покупателей – бесконечен.
каждый вызов обязательно будет обслужен. Здесь все корректно, поскольку каждая единица товара будет продана и каждый покупатель обслужен.
Допущения:
Поток товаров данного наименования для данного магазина – простейший с параметром ( - интенсивность).
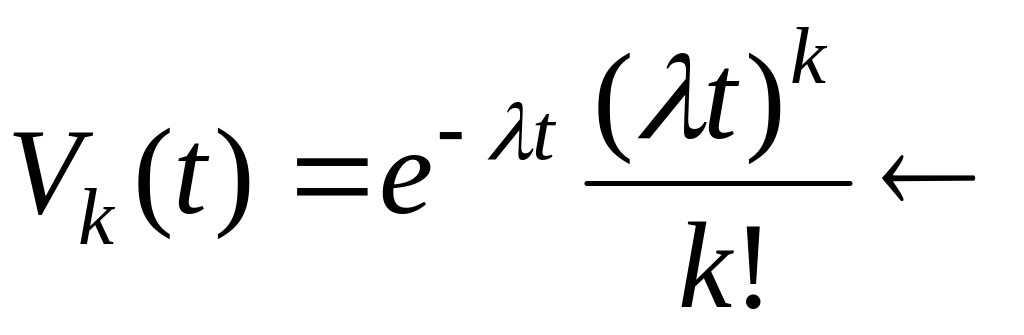пуассоновский
.Поток покупателей - простейший с параметром .
- вероятность того, что за время
будет ровно
покупателей.
;
.
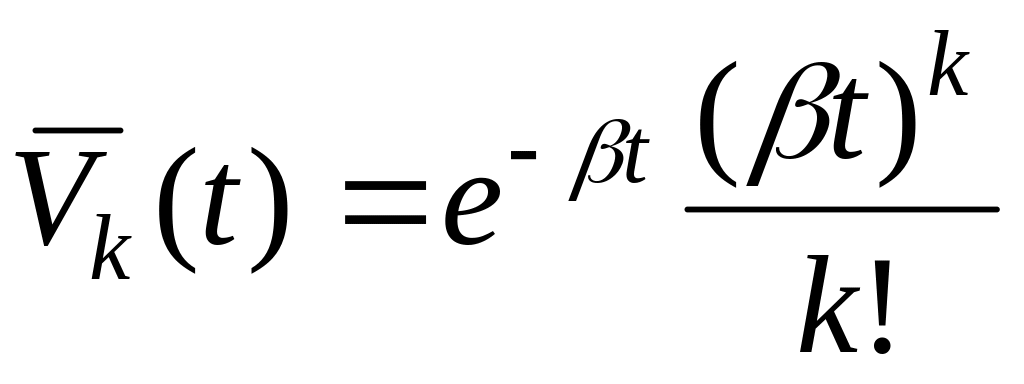- длина промежутка между моментами
прихода двух последовательных
покупателей.
распределена показательно с параметром
.
(
- интенсивность потока покупателей).
В одни руки – одна единица товара.
- вероятность того, что спрос будет предъявлен на единиц товара, то есть и спрос имеет пуассоновский вид.
Вводим понятие линии; отвечаем, сколько их.
Что значит - линия занята?
Что такое обслуживание?
Какой у обслуживания закон?
Состояние СМО.
Условная линия – спрос.
есть спрос,
- нет спроса. Спрос есть – линия свободна
(есть люди, готовые унести товар), спроса
нет – линия занята (некому обслуживать
единицы товара).
- время обслуживания.
За время :
линия не освободится.
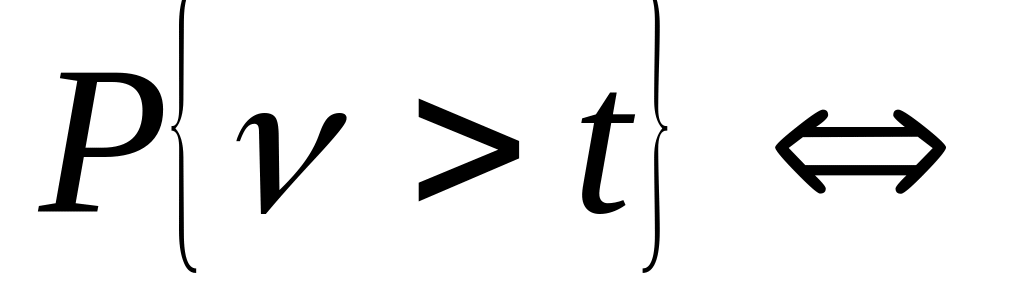«0 покупателей в промежутке
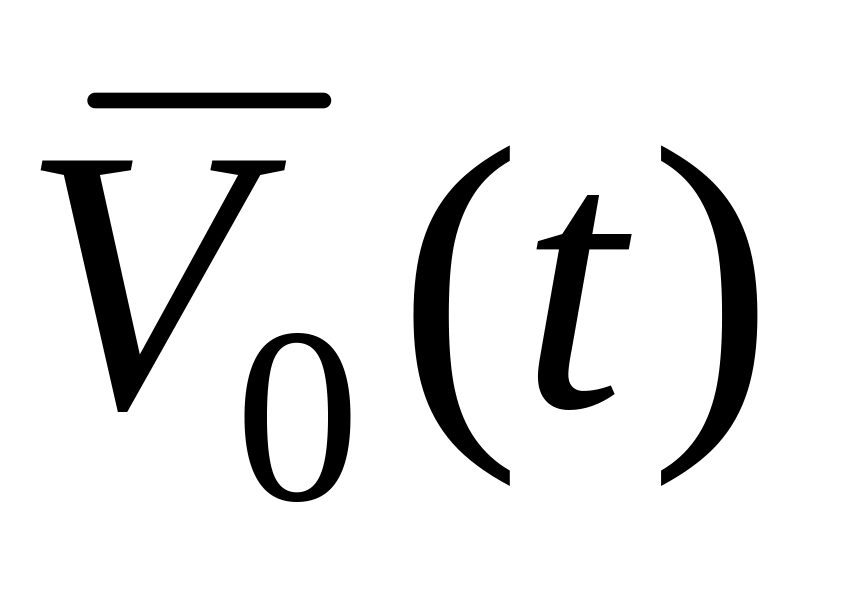
предыстория не играет роли.
Линия освободится в промежутке .
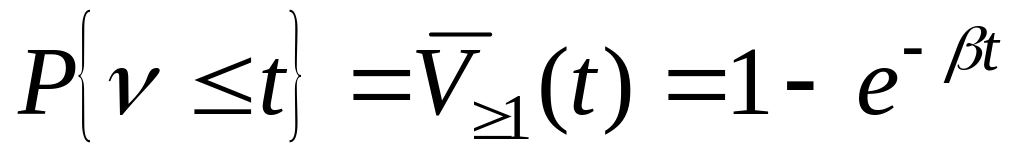
Состояние СМО? = размер запаса товаров.
- размер запаса.
└────┘
(6, 7, 8)
Поскольку нет физической линии, нет и
вызова на обслуживании.
- количество вызовов в системе.
.
- количество вызовов в очереди.
- количество вызовов на обслуживании.
количество занятых линий не равно
в этой СМО.
Состояние
на условной линии
Состояние на реальной линии
Обе очереди не могут быть одновременно положительными. Если существует одна очередь, то отсутствует другая.
Если товара нет, то не известно, свободна
линия, или нет (спрос может быть, а может
не быть).
означает, что товар в магазине отсутствует.
- доля времени нулевого состояния (товар
отсутствует).
- доля времени, когда товар присутствует.
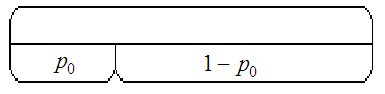
Поставим экстремальную задачу.
Пусть издержки управления запасами товаров в магазине состоят из:
а) Издержек хранения запасов товара в магазине.
б) Издержек вследствие дефицита.
Пусть
- издержки хранения единицы товара в
промежутке времени единичной длины.
Пусть
- издержки вследствие дефицита в единицу
времени.
- общее количество вызовов.
- издержки хранения,
- издержки дефицита,
- доля дефицита.
- коэффициент пропорциональности.
- среднее число вызовов в СМО.
; .
;
. (**)
Так как
(должно быть, чтобы сходилаь сумма
геометрической прогрессии)
выбираем при знаке «-» в (**)
,
.
Замечание: Функционирование стоянки такси. Поток: 1. Пассажиров. 2. Автомашин. Входящий поток – поток автомашин. - оптимальная интенсивность прибытия автомашин.