§ 5. Практические приложения модели сож

1. Ремонт телевизоров. СМО – ателье по ремонту, вызов – сломанный телевизор. Поток сломанных телевизоров неограничен,

. - время ремонта – случайная величина, распределенная показательно с параметром .

Данная СМО – СОЖ. - зависит от характера поломки.

Линия – мастер. Пусть - 5 мастеров; пусть .

- пропускная способность мастера, .

- Время обслуживания вызова = рабочего дня = 4 часа.

1 вопрос: справляется ли мастерская (СМО)?

Для этого сравниваем и 1. Если , то справляется, - не справляется.

очередь не растет бесконечно.

Коэффициент загрузки - доля времени, когда линия занята.

2 вопрос: среднее число занятых работой мастеров.

в среднем занято 4 мастера.

3 вопрос: Какова вероятность того, что в момент поступления очередного вызова все мастера окажутся:

а) свободными:

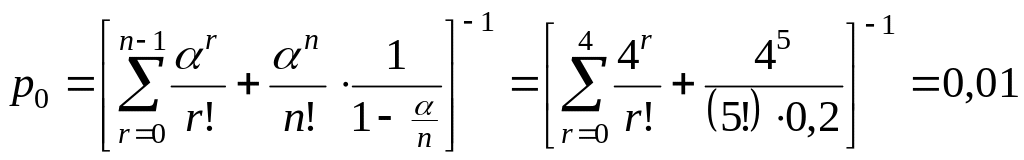
б) занятыми:

4 вопрос: Вероятность того, что телевизоры, сданные в течение рабочего дня, не начнут ремонтировать в течение этого же рабочего дня.

5 вопрос: Каково среднее время ожидаемого ремонта? рабочего дня.

6 вопрос: Вероятность того, что время ожидания превзойдет среднее время ожидаемого ремонта.

7 вопрос: Через какое время в среднем заказчик получает исправный телевизор.

рабочего дня часов.

8 вопрос: Среднее число телевизоров, ожидающих ремонта?

II. Расчет объема памяти информационно-логической машины (илм).

Вызов – сообщение на обработку. Входящий поток – поток сообщений. Его можно считать простейшим и неограниченным с параметром (сообщений в минуту).

Конструкция машины позволяет обрабатывать одновременно только одно сообщение, то есть . Обслуживание – обработка. - время обработки сообщений – распределено по показательному закону с параметром (сообщений в минуту). зависит от характера обработки.

Если в момент получения очередного сообщения ИЛМ оказывается занята, то это новое сообщение записывается в буферную память. Пусть - длина промежутка времени: если в течение этого промежутка сообщение в обработку не поступит, то оно отбрасывается. Требуется выбрать объем памяти . В этой модели допускаются любые размеры очереди. Аргументы к использованию СОЖ – так как заранее не известно, где «рвать» очередь, допускаются любые размеры очереди. Несмотря на это, большие размеры очереди маловероятны. Это означает, что очередь конечна.

Выберем условие, из которого может быть найден исходный размер памяти. Для этого заметим, что сообщение может теряться по двум причинам:

1. Оно устаревает (обесценивается). .

2. Буферная память заполнена. Длина очереди .

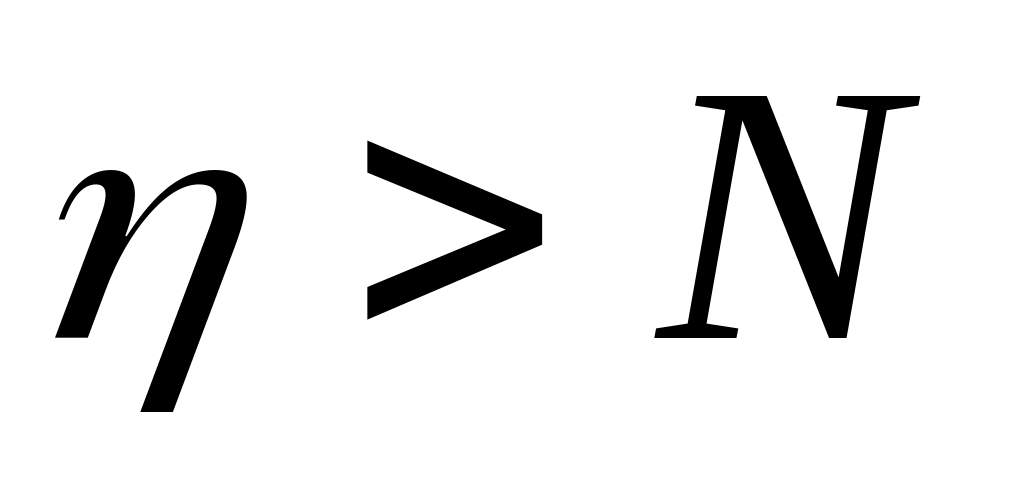Целесообразно считать, что если сообщение теряется, то это - следствие обеих вышеуказанных причин. Для этого необходимо, чтобы вероятности этих причин совпадали.

будем искать .

1. Ищем левую часть. 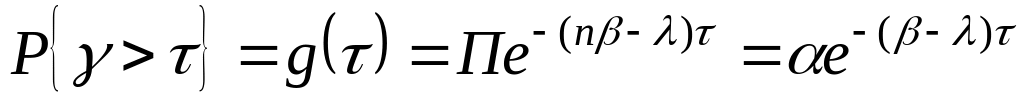, (2)

так как , .

геометрическая прогрессия

Поскольку система однолинейная, . (3)

Теперь приравниваем и ((2) и (3)).

. Хотим найти : логарифмируем: ;

, , так как , так как