Теория массового обслуживания

1. Гнеденко, Коваленко «Введение в теорию массового обслуживания», М., Наука, 1987 г.

2. Саульев «Математические модели ТМО», М., Статистика, 1979 г.

3. Розенберг, Прохоров «Что такое ТМО?», Советское радио, 1965 г.

4. «Научное управление запасами». Глава 21. Наука, 1967 г.

Введение в тмо

§ 1. О задачах тмо

ТМО – приложение (раздел) теории вероятностей (название дал академик Хинчин А. Я.). На Западе аналог – теория очередей. Основоположник теории – Эрланг. Затем свой вклад в становление ТМО сделали шведский математик Пальм, Александров, Хинчин, Марков.

Первоначально в качестве системы массового обслуживания (СМО) рассматривалась АТС. Количество линий связи конечно. Количество вызовов и длины разговоров – случайные величины.

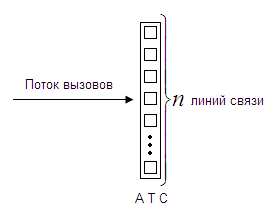
Если существует свободная линия, то поступивший вызов её занимает. Если в момент поступления вызова все линии заняты, то его дальнейшая «участь» зависит от типа СМО. Различают 3 типа СМО:

1. СМО с отказом (потерей) – если все линии заняты, то вызов получает отказ в обслуживании.

2. СМО с ожиданием – вызов становится в очередь; для системы не теряется и будет обслужен, когда подойдет его очередь.

3. Смешанные СМО (комбинация СМО с отказом и СМО с ожиданием) – в данной системе допускаются отказы (в случае, если длина очереди ограничена и в момент поступления вызова в ней заняты все линии) и ожидания. Пример: системы с ограниченной очередью (числом мест ожидания).

Основные задачи тмо

1. Нахождение стационарного состояния – вероятностей отдельных состояний СМО в установившемся режиме независимо от времени.

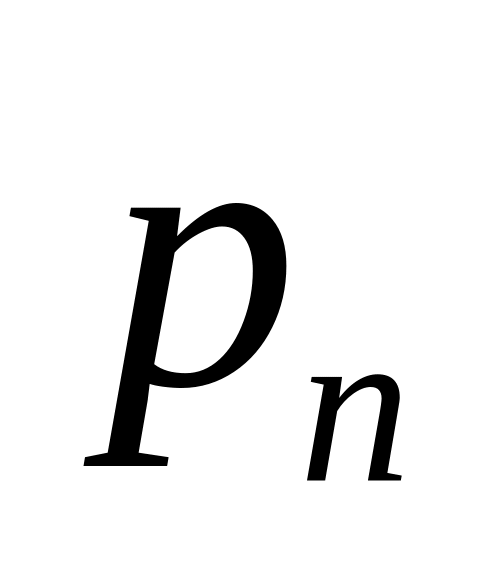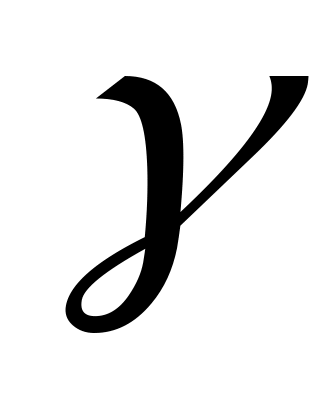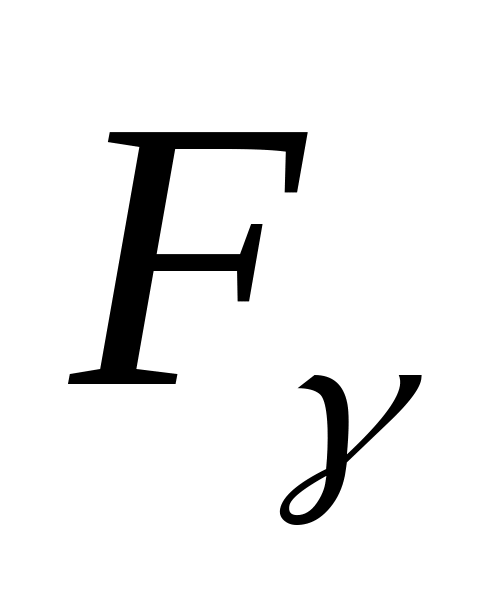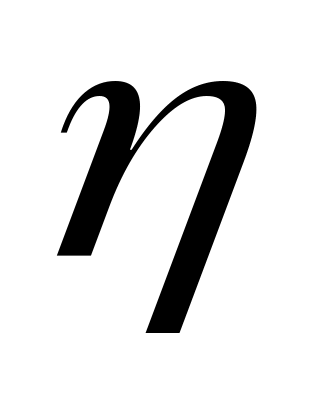2. Нахождение показателей эффективности функционирования данной СМО. Для СМО с отказом основным показателем является (вероятность отказа в обслуживании), для СМО с ожиданием изучается (время ожидания обслуживания вызова в очереди) (ищем функцию распределения ) и (длина очереди - дискретная случайная величина). Тогда показателями эффективности являются 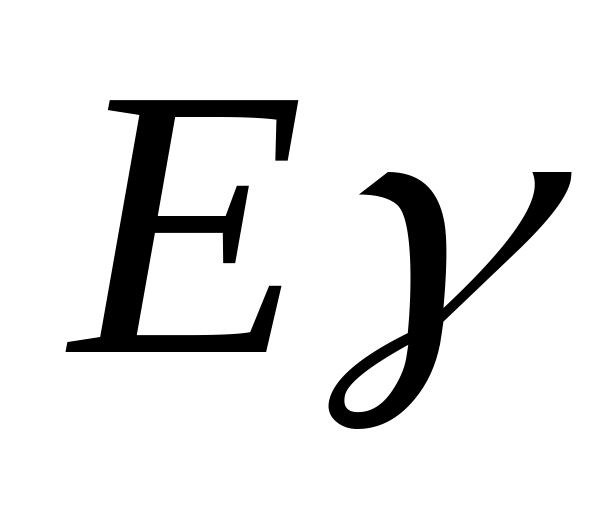- среднее время ожидания обслуживания в очереди, 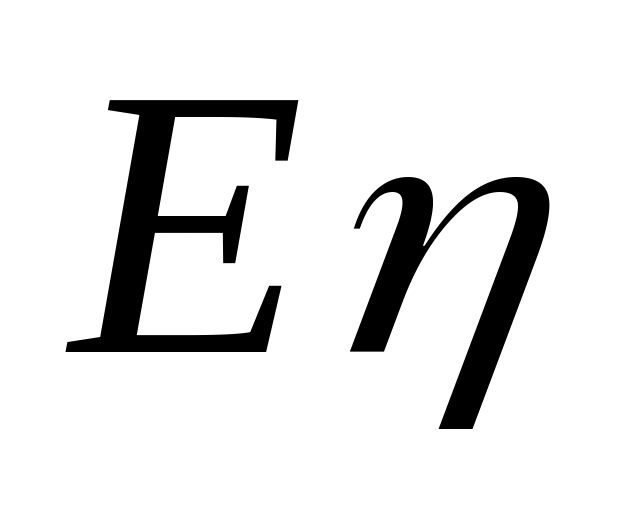- средняя длина очереди. Для смешанных СМО применяются показатели СМО с отказом и СМО с ожиданием, поскольку существуют , , .

3. Изучение закономерностей образования очередей (в СМО с ожиданием и в смешанных СМО, то есть там, где допускаются очереди). Необходимо найти условия, при которых очередь ведет себя естественным образом; нахождение условия, при котором очередь растет, то есть СМО не справляется с обслуживанием, и, соответственно, условия, при котором СМО справляется с обслуживанием (очередь то уменьшается, то растет).

4. Расчет рационального числа линий ( 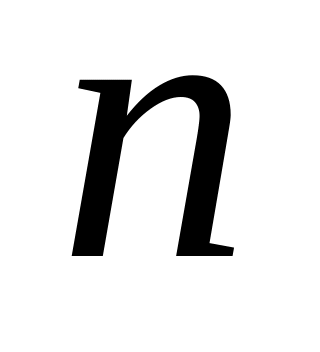) в пучке в данной СМО. На практике число линий должно быть некоторым конечным числом. Встает вопрос о том, как выбрать n. Следует учитывать то, что интересы клиентов и интересы СМО отличаются.

   1. С точки зрения вызовов – желательно, чтобы было большим, так как это приводит к улучшению качества обслуживания входящего потока: .

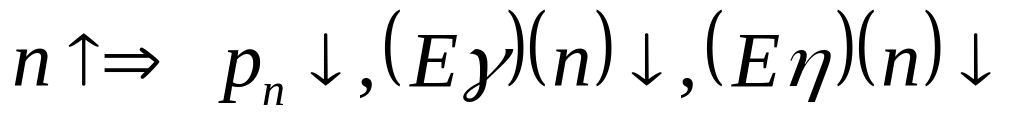• В СМО с отказом: если вероятность отказа уменьшается, то входящий поток полнее обслуживается.

• В СМО с ожиданием: чем больше в пучке, тем меньше времени затрачивается на стояние в очереди и уменьшается сама очередь.

2. С точки зрения самой СМО – число не должно быть слишком большим. Чрезмерно большое число линий повлечет уменьшение их загрузки, то есть увеличится простой линий необходим поиск «золотой середины».

Примеры:

1. Выбор числа продавцов или касс.

2. Расчет числа причалов в порту, посадочных полос на аэродроме.

3. Расчет количества оборонительных средств для определенного объекта.

4. Расчет запаса товара в магазине.