
- •Учебное пособие
- •Предисловие
- •Список основных обозначений
- •Выдающиеся ученые, создатели основ механики
- •ВВЕДЕНИЕ
- •1. МАТЕМАТИЧЕСКИЕ СВЕДЕНИЯ
- •1.1. Матрицы и векторы
- •1.2. Конкатенация матриц и линейных функций
- •1.3. Перепроецирование векторов и тензоров второго ранга
- •1.4. Решение системы алгебраических линейных уравнений MATLAB
- •2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- •2.1. Инерциальные системы отсчета
- •2.2. Поступательные (невращающиеся) система отсчета
- •2.4. Пример
- •2.5. Второй закон динамики в кинетостатической форме Даламбера
- •2.6. Закон динамики относительного движения
- •2.7. Уравнения относительного движения в форме Даламбера
- •2.8. Основной закон динамики относительного движения
- •2.9. Случай поступательного движения системы отсчета
- •2.10. Случай поступательной системы отсчета с началом на поверхности Земли
- •2.11. Прямолинейное движение материальной точки во вращающейся системе отсчета
- •3. ДИНАМИКА ТВЕРДОГО ТЕЛА
- •3.1. Геометрия масс твердого тела
- •3.2. Статические моменты массы и координаты центра масс тела
- •3.3. Осевые моменты инерции и радиусы инерции тела
- •3.4. Осевые моменты инерции площади поперечного сечения тела
- •3.5. Центробежные моменты инерции твердого тела
- •3.6. Перепроецирование вектора с применением матрицы поворота
- •3.7. Тензор инерции в точке твердого тела
- •3.8. Угловая скорость сферического движения тела
- •3.9. Кинетический момент сферического движения тела
- •3.10. Динамические уравнения Эйлера
- •3.11. Элементарная теория гироскопа
- •3.12. Динамика произвольного движения твердого тела
- •4.1. Сведения из статики
- •4.2. Момент силы и пары сил, расположенных в плоскости
- •4.3 Бивектор плоской системы сил
- •4.4. Уравнения равновесия плоской системы сил
- •4.5 Бивектор и M-функции пространственной системы сил
- •4.6. Матричное уравнение равновесия пространственной системы сил
- •4.7. Бивекторы реакций опор
- •4.8. Пример конкатенации матриц в матричном уравнении равновесия
- •4.9. Кинетостатическое матричное уравнение произвольного движения тела
- •5. ДИНАМИКА ГОЛОНОМНЫХ МЕХАНИЧЕСКИХ СИСТЕМ
- •5.1. Фазовый вектор системы (вектор состояния системы)
- •5.2. Кинетическая энергия твердого тела и голономной стационарной одностепенной системы
- •5.3. Мощность силы
- •5.4. Работа и потенциальная энергия
- •5.5. Обобщенная сила одностепенной голономной стационарной системы
- •5.6. Обобщенная сила нестационарной одностепенной системы
- •5.7. Работа обобщенной силы одностепенной стационарной системы
- •5.8. Идеальные связи и реакции связей
- •5.9. Уравнение Лагранжа для одностепенной стационарной голономной системы
- •5.10. Уравнение Лагранжа для голономной нестационарной одностепенной системы
- •6. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- •6.1. Уравнения Лагранжа для голономной стационарной системы
- •6.2.Уравнения равновесия стационарной системы в обобщенных координатах
- •6.3. Матричная форма уравнений Лагранжа
- •6.4. Матричное уравнение Гамильтона
- •6.5. Теорема о движении центра масс механической системы
- •6.6. Теорема об изменении количества движения механической системы
- •6.7. Теорема импульсов
- •6.8. Теорема об изменении кинетической энергии
- •6.9. Теорема об изменении кинетического момента механической системы
- •Приложение
- •Равновесие плоской системы сил
- •Равновесие пространственной системы сил
- •Динамика относительного движения материальной точки
- •Литература

Q(x) x=0 = 0 −cf + 23 mg = 0 f = 2c3 mg
Подставляя выражение статической деформации f в обобщенную силу получаем окончательно: Q = −cx . Динамическое уравнение колебаний имеет вид:
&&x + k |
2 |
|
|
& |
|
|
|
|
x = 0 , с начальным состоянием x(0) = l − f , x(0) = v0 . |
|
|||||
Решение полученной начальной задачи Коши имеет вид: |
|
||||||
|
|
x = x(0)cos(kt) + |
v0 |
sin(kt) = (l − f )cos(kt) + |
v0 |
|
sin(kt). |
|
|
k |
k |
||||
|
|
|
|
|
|||
Пример 2. Решить предыдущую задачу при дополнительном условии, что наклонная поверхность вибрирует в вертикальном направлении с ускорением aO = Acos pt j1 , где орт j1 направлен вертикально.
Решение. В этом случае следует приложить в центре масс каждого звена переносную силу инерции Sek = −mk aO (наряду с силой Gk = mk g ), после этого систему отсчета Oxy можно условно считать неподвижной (инерциальной). Приложив в центре масс системы корпус-колеса силу GO = m(g −aO )
(вместо силы G |
= mg ), находим Q = P / x = −cx + 3 / 2 m(g −aO ). В результа- |
|||
|
|
|
& |
|
те получаем динамическое уравнение колебаний вида |
|
|||
&& |
2 |
x −h −a1 cos pt = 0 при a1 = mA |
3 2mпр , |
|
x + k |
|
|||
имеющее дополнительное гармоническое слагаемое.
5.10. Уравнение Лагранжа для голономной нестационарной одностепенной системы
Геометрическая связь в механической системе называется нестационарной, если она записывается в виде функционального уравнения, содержащего параметр t , т.е. если она изменяется с течением времени. Примеры нестационарных связей: математический маятник на нити переменной длины l=5t , прибор на платформе, совершающей заданное во времени программное движение, механизм с заданными кинематическими уравнениями движения одних звеньев относительно других. Голономная система называется одностепенной нестационарной, , если она подчинена хотя бы одной нестационарной связи наряду со стационарными связями, но при этом сохраняет одну степень свободы. Положение одностепенной механической системы определяется одной выбираемой обобщенной координатой q в каждое конкретное мгновение t .
В стационарной голономной системе радиус-вектор ri любой i-ой точки
системы можно найти на основании геометрического изображения объекта (желательно изображать положение q > 0) , как функцию обобщенной коор-
динаты ri = ri (q) . Скорость точки определяется функцией vi = ∂ri ∂q q& .
88

Для нестационарных систем приходим к более сложным выражениям
ri = ri (q,t) , в связи с чем скорость v |
|
содержит дополнительное слагаемое, не |
|||||||
|
|
|
i |
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
содержащее q : |
|
|
|
|
|
|
|
|
(5.47) |
& |
|
+∂ri |
∂t |
, где |
|
= ∂ri |
& |
||
vi = ∂ri ∂q q +∂ri |
∂t = vi |
vi |
∂q q . |
|
|||||
Составляющую vi скорости vi , вычисляемую при фиксированных значениях
параметра t в нестационарной связи, получаемую за счет изменения только обобщенной координаты q , назовем виртуальной скоростью.
Из выражений (5.47) следует, что кинетическая энергия системы имеет трехчленную структуру и является квадратным полиномом относительно обобщенной скорости с переменными или постоянными коэффициентами, которые обозначим символами ak :
|
1 |
&2 |
& |
|
ak = ak (q,t),k = 0,1,2 . |
(5.48) |
T = |
2 a2q |
+ a1q + a0 |
при |
|
||
Мощность системы приложенных к механической системе сил будем вычислять на виртуальных скоростях точек приложения сил, т.е. при условии, что в нестационарных связях параметр t закреплен в своем положительном значении. При этом не будем принимать во внимание не имеющие мощности идеальные реакции нестационарных и стационарных связей при закрепленном параметре t в связях. Имеем выражение виртуальной мощности системы сил:
P* = ∑Fi |
vi* +∑M |
j ω |
*j |
(5.49) |
Здесь силы Fi и моменты пар M j в общем случае могут зависеть от реальных скоростей vi и угловых скоростей ωj , а также - от координат и от времени.
Выразив в выражении (5.49) виртуальные скорости vi* , ω*j , а также действительные скорости и координаты через фазовые переменные q& и q , полу-
чим мощность P* (q&, q,t) ,в которой обязательно имеется общий множитель q&.
Обобщенной силой нестационарной голономной одностепенной меха-
нической системы называется отношение виртуальной мощности системы сил (мощности системы сил на виртуальных скоростях) к обобщенной скорости:
Q = P |
* |
& |
* |
|
|
|
|
* |
(5.50) |
|
|||||||||
|
|
|
|||||||
|
/ q, при P = ∑Fi |
(vi , ri ,t) vi |
+ ∑M j ω j |
|
|||||
В общем случае Q есть функция трех параметров: Q =Q(q&, q,t). В (5.50) силы зависят от действительных (не виртуальных) скоростей.
Уравнение Лагранжа для нестационарной (и стационарной) одностепенной системы имеет вид:
d |
∂T |
|
|
∂T |
(5.51) |
|
|
|
& |
|
− |
∂q |
= Q , |
|
||||||
dt |
∂q |
|
|
|||
|
|
|
|
|
|
89 |

т.е. полная производная по времени от обобщенного импульса ∂T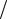 ∂q&, уменьшенная на величину ∂T
∂q&, уменьшенная на величину ∂T ∂q равна обобщенной силе системы приложенных
∂q равна обобщенной силе системы приложенных
сил, определяемой по формуле (5.50) через мощность реальных сил на виртуальных скоростях.
Выполнив процедуры дифференцирования трехчленного выражения кинетической энергии (5.48), указанные в уравнении (5.51). Получим окончательно динамическое уравнение в форме ОДУ второго порядка:
|
|
1 |
|
2 |
∂a2 |
|
∂a2 |
q +b |
|
q |
|
|
+ q |
|
|
&& |
|
2 |
& |
|
∂q |
& |
∂t |
|
|
|
|
||||
|
при ak |
= ak (q,t), |
|||||
|
∂a1 |
|
∂a0 |
−Q |
(5.52) |
+ |
− |
= 0, |
|||
|
∂t |
|
∂q |
|
|
k = 0,1,2, b = a2−1
К закону динамики нестационарной механической системы вида (5.52) присоединим начальные условия, т.е. начальный фазовый вектор, дающий
информацию о предистории движения |
|
|
|
|
(5.53) |
||||||||||||
|
|
q(0) = q0 , |
q(0) = q0 |
или [q(0), q(0)] =[q0 , q0 ] |
|
|
|||||||||||
|
|
& |
|
|
& |
|
|
|
|
|
|
& |
& |
|
|
|
|
|
Математическую модель движения рассматриваемой механической сис- |
||||||||||||||||
темы (5.52)-(5.53), можно записать в нормальной форме Коши: |
(5.54) |
||||||||||||||||
& |
|
∂a0 |
|
∂a1 |
|
∂a2 |
|
1 |
|
2 ∂a2 |
|
& |
|
* |
|
−1 |
|
u = b Q + |
∂q |
− |
∂t |
−u |
∂t |
− |
|
u |
∂q |
|
, q = u, |
при Q = P |
|
/ u, |
b = a2 |
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
u(0) =u0 , |
q(0) = q0 |
|
|
|
|
(5.55) |
||||
Вместо начальных условий (5.53), (5.55) могут быть заданы граничные
условия, или условия периодичности искомого решения. Пример
Рис. 18 Вибрация электродвигателя
90

Электродвигатель массой m1 , установлен на пружинах общей жесткости с2 , с массой пружины m2 . Радиусы инерции каждого из четырех направляющих колес i3 , радиусы колес r3 . На оси О двигателя установлен неуравновешанный маховик массой m4 с расстоянием до центра масс r4 , радиус инер-
ции маховика относительно оси О равен i4 , маховик равномерно вращается согласно кинематическому уравнению φ= ω4 t , при ω4=2. Задан момент вязкого трения на осях каждого из четырех колес M3= b3 ω3 . Составить динамическое уравнение устройства.
Решение
Уравнением ϕ= ω4t =2t задана нестационарная связь. Пружины не соз-
дают связей, они лишь создают силы и имеют инерционность, которую со-
гласно методу Рэлея учтем, прибавив к массе m1 двигателя третью часть массы пружин m2 [12]. Имеем нестационарную механическую систему с одной
степенью свободы, в которой за обобщенную координату примем направлен-
ное вверх смещение от положения оси О, соответствующего недеформиро-
ванному состоянию пружины.
|
|
|
Фазовый вектор ситемы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
На рис.18 показано поло- |
|||||||||||||||||||||||||||
|
|
|
|
V=[v,y] при v = y . |
|
||||||||||||||||||||||||||||||||||||||||||||
жительное кинематическое состояние системы, |
когда v>0 , |
y>0 . Получим |
|||||||||||||||||||||||||||||||||||||||||||||||
динамическое уравнение. Выразим силы и скорости |
через фазовые коорди- |
||||||||||||||||||||||||||||||||||||||||||||||||
наты v , y . Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ω |
|
= |
v |
, |
|
v = v |
+v |
|
|
при v |
|
=ω r |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
3 |
|
|
|
, v = vj |
, v |
|
OC, |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
r3 |
|
|
|
C |
|
CO |
|
|
|
|
|
|
CO |
|
|
4 |
4 |
|
|
|
|
|
|
|
|
CO |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.56) |
|||
ω |
3 =ω3k , F2 = −c2 y j , M3 = −b3ω3 k = −(b3v / r3 )k , |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
1 = −m1g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
G |
j |
, G |
4 = −m4 g |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Двойная кинетическая энергия устройства: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
2T |
|
|
1 |
m2 |
|
|
2 |
|
|
|
|
2 |
|
2 |
|
2 |
+ m4 (v |
2 |
|
|
|
|
|
|
|
|
|
2 |
2 |
) |
|
||||||||||||||
|
|
|
|
= m1 + |
3 |
v |
|
|
+ m3i3 v |
|
/ r3 |
|
|
+ 2v vCO +i4ω4 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
где v vCO = −vω4r4 sin(ω4t) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
Отсюда получаем кинетическую энергию в форме квадратного полино- |
||||||||||||||||||||||||||||||||||||||||||||||
ма относительно v : |
|
|
|
|
|
|
|
|
|
|
1 a v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.57) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T = |
+ a v + a |
, |
|
|
|
|
|
|
|
|
||||||||||||||
при обозначениях |
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.58) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 = m1 + m2 /3 + J3 / r32 + m4 , |
|
|
|
h4 = m4r4ω4 , |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = −h sin(ω |
t), |
|
a |
= m i2ω2 |
/ 2, |
|
ω |
4 |
= const |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
0 |
4 4 |
4 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Частные производные от коэффициентов, входящие в (5.52) |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂a2 = 0, |
|
|
|
∂a1 |
= −h ω |
4 |
cos(ω |
t), |
∂a2 |
= 0, |
∂a0 = 0 |
(5.59) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
∂t |
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
∂t |
|
|
|
|
∂y |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Обобщенная сила Q |
по обобщенной скорости |
|
& |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
v = y находится через |
||||||||||||||||||||||||||||||||||||||||||||||
вычисление виртуальной мощности системы всех приложенных сил на вир91

туальных скоростях точек приложения сил. При этом в выражениях сил зависящих от скоростей не следует заменять действительные скорости на виртуальные. Не принимаем во внимание крутящий момент электродвигателя вме-
сте с моментом трения в подшипнике O , осуществляющих нестационарную
связь – программное движение кривошипа, поскольку их мощность на виртуальном движении при фиксированном t (т.е. при ϕ = const ) равна нулю.
|
|
|
|
|
|
|
|
|
|
подсчитываем на виртуальной скорости v * = v . Центр |
||||||||||||||||||||||||||
Мощность силы G |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
масс пружин амортизатора имеет скорость v / 2 . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P* = G |
V |
+G V / 2 +G V + F V +4M |
3 |
ω |
3 |
= −(G +G / 2 +G + F + 4M |
3 |
/ r )V |
||||||||||||||||||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
1 |
2 |
|
4 |
2 |
4 |
|
|
|||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.60) |
||||||||
|
|
|
|
|
|
|
|
|
Q = P |
* |
|
|
|
& |
|
|
|
+G1 |
+G2 / 2 +G4 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
/ v = − |
y +c2 y |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Подставляя в уравненние Лагранжа (5.52) выражения (5.59),(5.60) по- |
|||||||||||||||||||||||||||||||||||
лучаем динамическое уравнение устройства: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
&& |
|
|
|
b3 |
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
+G2 / 2 +G4 −h4ω4 cos(2t) |
= 0, |
b = a2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
y |
+b |
y + c2 y +G1 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
r3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Окончательно имеем линейное неоднородное ОДУ второго порядка с
постоянно действующими периодическими возмущениями следующей структуры:
&& |
& |
2 |
y +h0 |
−h cos( pt) = 0, |
0 ≤ n < k |
(5.61) |
y |
+2ny + k |
|
|
при обозначениях
n =b /(2r3a2 ), k = c2 / a2 , h0 = (G1 +G2 / 2 +G4 ) / a2 , h = h4ω4 / a2
Общее решение уравнения (5.61) состоит из частного периодического решения, имеющего гармоническую и постоянную составляющие, и общего решения однородного уравнения с двумя константами С и β :
y = H cos( pt −α) −h0 / k |
2 |
+Ce |
−nt |
cos(k1t |
− β), k1 = |
k |
2 |
−n |
2 |
(5.62) |
||
|
|
|
|
|
||||||||
H = |
|
h |
, |
α = arccos(h−1H (k2 − p2 )) |
|
|
|
|
||||
(k2 |
− p2 )2 +4n2 p2 |
|
|
|
(5.63) |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Константы |
С и β |
определяются |
через |
начальные |
условия |
|||||||
y(0) = y0 , y&(0) = v0 y посредством подстановки их в общее решение (5.62) и в
производную от него.
Согласно уравнению (5.62) система совершает двухчастотные колеба-
ния около положения y = −h / k2 с собственной циклической частотой k1 и
вынужденной частотой p . При этом амплитуда собственных колебаний
уменьшактся по показательному закону e−nt с коэффициентом затухания n , обусловленным вязким трением. В результате любое движение системы
92
асимптотически приближается к одночастотному колебанию, не зависящему от начальных условий, подчиненному уравнению:
y = H cos( pt −α) + yСТ при yСТ = −h0 / k2 |
(5.64) |
Иными словами, система совершает гармонические колебания согласно формуле (5.64), асимптотически устойчивые относительно начальных возмущений в том смысле, что любой переходный процесс, начинающийся с состояния y(0) = y0 , y&(0) = v0 , асимптотически переходит в периодические колеба-
ния относительно статического положения y = yСТ с постоянной амплитудой
H , с частотой, равной частоте возмущающей силы и с фазой, смещенной на величину α от фазы кинематического возмущения.
Примечание В случае нестационарной одностепенной механической системы уравнение Лагранжа и уравнение энергии T& = P приводят к различ-
ным дифференциальным уравнениям. В данном примере из уравнения T& = P
получается дифференциальное уравнение, содержащее мощность крутящего момента. Такое уравнение можно использовать для вычисления крутящего момента, обеспечивающего выполнение нестационарной связи, но прежде следует применить уравнение Лагранжа и получить решение (5.64).
93
