4.9.Кинетостатическое матричное уравнение произвольного движения тела

Определение движения абсолютно твердого тела по заданной приложенной системе сил и заданному начальному кинематическому состоянию принято называть второй задачей динамики. Определение неизвестных приложенных сил по известным кинематическим уравнениям движения называется первой задачей динамики. Имеются также смешанные задачи и более сложные задачи оптимального управления.

В двух динамических матричных уравнениях (3.51) и (3.56) изменим все знаки на противоположные. Получим при очивидных обозначениях два матричных уравнения равновесия:

Mc + Mcин =O3 , R + Rин =O3 при Mcин = −ωJcω% −ω&Jc , Rин = −mac

Здесь считаем, что все вектор-строки даны в проекциях на оси системы Oxyz , жестко связанной с телом.

Разобьем систему приложенных сил на систему неизвестных реакций связей и систему известных нагрузок, Mc = Mreact + Mdet , R = Rreact + Rdet и обозначим бивекторы этих сил через Wreact и Wdet .

Объединив два матричных уравнения в одно, получим следующее утверждение.

Теорема о кинетостатическом равновесии сил. В системе координат Cxyz , жестко связанной с твердым телом, все приложенные к телу силы и силы инерции удовлетворяют матричному кинетостатическому уравнению равновесия

т.е. равна нуль-строке сумма бивекторов реактивных, известных нагрузочных и известных инерционных сил. Здесь все вектор-строки записаны в проекциях на оси подвижной системы Cxyz.

Из уравнений (4.40) следует, что движение и состояние покоя тела вполне определяются, если известен бивектор системы приложенных сил, тензор инерции тела, радиус-вектор центра масс и масса тела.

Замечание. В случае сферического либо вращательного движения тела можно начало O сцепленной с телом системы Oxyz взять в неподвижной точке тела

где Jo - постоянный тензор инерции в сцепленной системе Oxyz.

Покажем составление кинетостатического матричного уравнения абсолютно твердого тела на следующей задаче.

66

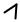F1

Рис. 16 Вращательное движение неуравновешанного тела

Задача. Тело массой m произвольной формы (неуравновешенный маховик) (Рис. 16) вращается в инерциальной системе O1x1y1z1 равноускоренно вокруг горизонтальной оси O1z1 согласно заданному уравнению φ = ω0t + εt2/2. Ось Ox системы Oxyz, сцепленной с телом, направлена на центр масс C, известен радиус-вектор центра масс rC = [b 0 0] и тензор инерции тела в точке O

J0 = [Jx Jxy Jxz ; Jyx Jy Jyz ; Jzx Jzy Jz]

Определить вращающий момент M обеспечивающий заданное движение и реакции F1, F2 опор в сцепленной системе Oxyz.

Решение. Угол φ отсчитываем от отвесной линии. Считаем известными векторы ω = ϕ&k , ε = ϕ&&k , силу G = mg расстояние OC = b до центра масс,

расстояния OO1=b1, OO2=b2. Неизвестны векторы: M = Mk — вращающий момент, F2 O1z1 и F1 - реакции цилиндрического и сферического шарниров.

Величины в виде векторов-строк в системе Oxyz:

ω = [0 0 ωz], ε = [0 0 εz], G = [G cosφ, – G sinφ, 0], F1 = [X1 Y1 Z1], F2 = [X2 Y2 0], M = [0 0 M], r1 = [0 0 –b1], r2 = [0 0 b2], rC = [b 0 0].

Здесь пару сил с подлежащим определению моментом относим к неизвестным реакциям связей. Применим матричное кинетостатическое уравнение:

Wreact + Wdet + Winert = zeros(1, 6).

Здесь Wreact - сумма бивекторов реакций связей, включая бивектор вращающей пары, обеспечивающей нестационарную связь – кинематические уравнения вращения, Wdet - сумма бивекторов известных приложенных сил, которые находятся по правилам , показанным в разделе "уравнения равновесия тела". Winert — бивектор сил инерции тела, образованный горизонтальным сцеплением главного момента – строки и главного вектора - строки инерционных сил.

Имеем бивектор сил инерции в системе Oxyz с неподвижным полюсом O:

Winert =[−ωJCω% −εJO , −mrCω%2 −mrCε%],

или с применением M-функций, и переобозначением ω -> w, ε -> e:

Winert = [-w*JO*s33(w)–e*JO, –m*rC*ss331(w, e)].

MATLAB возвращает это выражение в форме шестиэлементной вектор-

строки:

Winert = [-wz2Jzy – eJzx , –wz2Jzx – εzJzy , – εzJz , mbwz2, –mbez , 0].

67

Бивектор единственной известной приложенной силы Wdet = G*s36(rC). В бивекторе неизвестных сил

Wreact = F1*s36(r1) + [X2 Y2]*sz26(r2)+Mz*[0 0 1 0 0 0].

выполним горизонтальную конкатенацию первых сомножителей в векторстроку искомых величин и вертикальную конкатинацию вторых сомножителей в блочную квадратную матрицу шестого порядка. Получим:

Wreact = V*K при V = [X1 Y1 Z1 X2 Y2 Mz], K = [s36(r1); sz26(r2); [0 0 1 0 0 0]].

Бивектор известных сил и моментов: L = G*s36(rC) + Winert.

Получаем кинетостатическое уравнение равновесия V*K+L=0. Отсюда, искомая вектор-строка неизвестных реакций возвращается функцией V = – L/K.

Таким образом, задача кинетостатики об определении динамических реакций связей может быть подменена статической задачей равновесия (покоя) тела в сцепленной системе Oxyz , но с дополнительными силами. После

того как вычеслен бивектор Winert , можно выполнить новый чертеж для эквивалентной задачи, на которой ось Ox остается отвестной, оси Oy и Oz гори-

зонтальны, сила G вращается по часовой стрелке по закону ψ = −ϕ , бивектор

Winert подразумеваем, но наносить его на чертеж нет необходимости, поскольку он уже вычеслен аналитически и вносится в уравнение без комментариев. На основании такого нового рисунка решается обычная задача статики о равновесии пространственной системы приложенных сил.

Напомним, что физический смысл кинетостатического уравнения (4.40) – равенство сил давления тела на систему связей (массовых сил инерции и сил тяжести) и противодействия связей такому давлению.

68