МІНІСТЕРСТВО ОСВІТИ І ТАУКИ УКРАЇНИ

ЧЕРКАСЬКИЙ ДЕРЖАВНИЙ БІЗНЕС-КОЛЕДЖ

(назва навчального закладу)

Пакет документів

для проведення комплексних контрольних робіт

з предмета

„Теорія ймовірностей та математична статистика”

Галузь 0501 „Інформатика та обчислювальна техніка”

Спеціальність 5.05010301 „Розробка програмного забезпечення”

Укладач: Ходаковська О.О.

Викладач ІІ категорії

Розглянуто та затверджено на засіданні

ЦК фундаментальних дисциплін

Протокол № 5 від 03.12.2012 р.

2012

1. Перелік питань

1. Висловлення. Логічні операції

2. Закони логіки висловлювань

3. Спеціальні форми подання булевих функцій

4. Мінімізація булевих функцій. Карти Карно

5. Предикати. Квантори. Формули логіки предикатів

6. Булеві функції: основні поняття та означення

7. Реалізація булевих функцій формулами

8. Алгебри булевих функцій

9. Аналіз і синтез релейно-контактних схем

10. Множини: основні поняття та означення

11. Операції над множинами.

12. Комп'ютерне подання множин

13. Відношення та їх властивості

14. Відношення еквівалентності. Відношення часткового порядку

15. Операції над відношеннями

16. Алгебраїчні операції та їх властивості. Поняття алгебраїчної структури

17. Найпростіші алгебраїчні структури. Кільця і поля

18. Означення та основні властивості подільності. Ділення з остачею

19. Найбільший спільний дільник двох чисел і алгоритм Евкліда

20. Найменше спільне кратне

21. Властивості конгруенцій за даним модулем

22. Властивості конгруенцій за різними модулями

23. Класи чисел за даним модулем

24. Повна і зведена система лишків. Функція Ейлера

25. Основні правила комбінаторного аналізу. Перестановки. Розміщення та сполучення

26. Біном Ньютона. Трикутник Паскаля. Метод математичної індукції

27. Основні означення та властивості графів

28. Деякі спеціальні класи простих графів

29. Способи подання графів (матриця інцидентності, матриця суміжності)

30. Шляхи та цикли. Зв'язність. Ізоморфізм графів

31. Ейлерів цикл у графі

32. Гамільтонів цикл у графі

33. Планарні графи

34. Розфарбовування графів

35. Основні означення та властивості дерев

36. Рекурсія. Обхід дерев. Бінарне дерево пошуку. Дерево прийняття рішень.

37. Бектрекінг (пошук із поверненнями). Каркаси (з'єднувальні дерева)

38. Мова та грамматики

39. Алгоритми

40. Автомати

2. Перелік практичних завдань

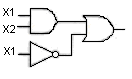
Практичне завдання № 1.

Провести аналіз логічного ланцюга:

Практичне завдання № 2.

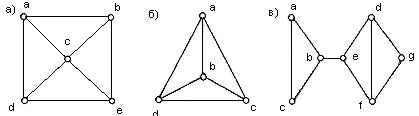
Визначити кількість вершин та дуг і знайти напівстепені входу й виходу для кожної вершини орієнтованого графа:

Практичне завдання № 3.

Методом математичної індукції довести подільність:

Практичне завдання № 4.

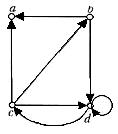
Знайдіть матриці інцидентності та матриці суміжності графа:

Практичне завдання № 5.

Провести аналіз логічного ланцюга:

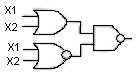
Практичне завдання № 6

Знайдіть матриці інцидентності та матриці суміжності графа:

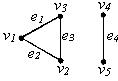
Практичне завдання № 7.

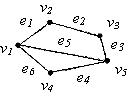
Знайти кількість вершин, ребер і степені кожної вершини неорієнтованих графів:

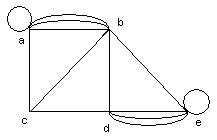
Практичне завдання № 8.

Знайти найбільший спільний дільник чисел: 2091 і 1681.

Практичне завдання № 9.

Для заданої матриці інцидентності знайдіть відповідний граф:

Практичне завдання № 10.

Знайти найбільший спільний дільник чисел: 588, 2058, 2849.

Практичне завдання № 11.

Знайдіть вершини й орієнтовані ребра для орієнтованого графа. Для кожної вершини визначте степінь входу й степінь виходу.

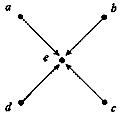
Практичне завдання № 12.

Знайти найменше спільне кратне чисел: 279 і 372.

Практичне завдання № 13.

Для заданої матриці суміжності знайдіть відповідний граф:

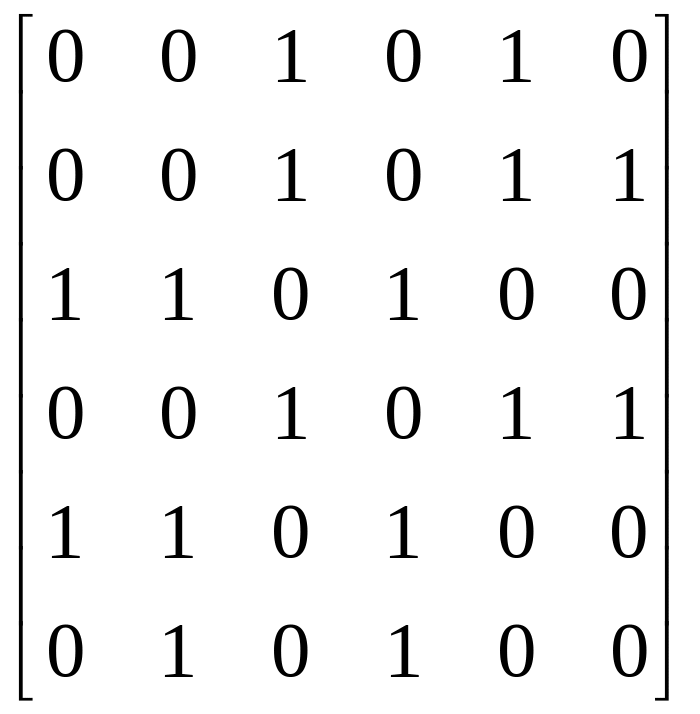
Практичне завдання № 14.

Знайти найменше спільне кратне чисел: 356, 1068, 1424.

Практичне завдання № 15.

Здійснити синтез логічної схеми для булевої функції: .

Практичне завдання № 16.

Знайдіть вершини й орієнтовані ребра для орграфів. Для кожної вершини визначте степінь входу й степінь виходу.

Практичне завдання № 17.

Знайдіть гамільтоновий цикл, якщо він існує, для даного графа.

Практичне завдання № 18.

Нехай дано відношення: , .

Визначити .

Практичне завдання № 19.

Перевірити наведений граф на планарність.

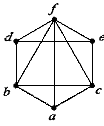
Практичне завдання № 20.

Побудуйте таблицю істинності для висловлення: .

Практичне завдання № 21.

Знайдіть вершини й орієнтовані ребра для орієнованого графа. Для кожної вершини визначте степінь входу й степінь виходу.

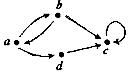
Практичне завдання № 22.

Побудуйте таблицю істинності для висловлення: .

Практичне завдання № 23.

Використайте карти Карно для спрощення висловлення: .

Практичне завдання № 24.

Задати простий граф за допомогою матриць інцидентності та суміжності.

Практичне завдання № 25.

Знайти диз’юнктивний розклад функції: .

Практичне завдання № 26.

Визначити, чи має граф ейлерів цикл. Якщо так, то зобразити його.

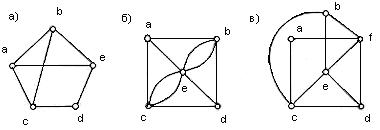
Практичне завдання № 27.

Довести рівносильність формул і , використовуючи тотожні перетворення і таблиці істинності: .

Практичне завдання № 28.

Зобразити орієнтований граф за матрицею інцидентності:

Практичне завдання № 29.

Побудуйте таблицю істинності для висловлення: .

Практичне завдання № 30.

Задати орієнтований граф за допомогою матриць інцидентності та суміжності.

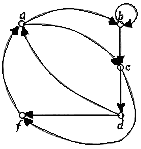
Практичне завдання № 31.

Довести рівносильність формул і , використовуючи тотожні перетворення і таблиці істинності: .

Практичне завдання № 32.

Чи має граф ейлеровий цикл?

Практичне завдання № 33.

Спростіть висловлення, яке представлене за допомогою карт Карно:

	1	0	0	1
	0	1	1	1
	0	0	0	0
	1	0	0	1

Практичне завдання № 34.

Зобразити неорієнтований граф за матрицею суміжності:

Практичне завдання № 35.

Знайдіть булевий вираз, який відповідає релейно-контактній схемі:

Практичне завдання № 36.

Нехай , , , .

Знайти наступні множини: ; ; .

Практичне завдання № 37.

Чи має орієнтований граф ейлеровий цикл?

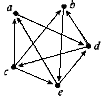
Практичне завдання № 38.

Перейти від заданої ДНФ до ДДНФ: .

Практичне завдання № 39.

Побудувати релейно-контактну схему, яка відповідає булевому виразу: .

Практичне завдання № 40.

Чи має даний граф гамільтоновий цикл?