4.2. Определение места судна по крюйс-расстоянию

При определении расстояния с помощью вертикального угла и отсутствии возможности пеленгования ориентиров, использования судовой радиолокационной станции при больших ошибках радиолокационного пеленга, место судна можно получить способом крюйс-расстояния.

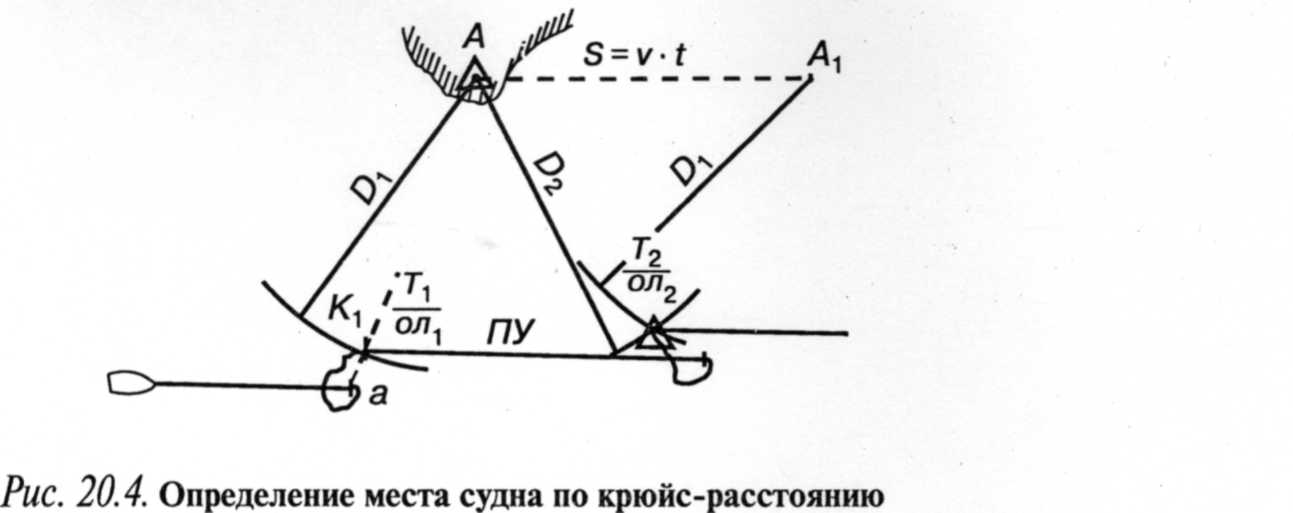
Практическое выполнение способа. Наблюдения, вычисления и прокладку при определении места судна по крюйс-расстоянию выполняют в следующем порядке. Измеряют расстояние D₁ до ориентира, фиксируя время Т₁ и отсчет лага ол₁. Рассчитывают истинное расстояние D₁ =D₁ + D и из ориентира проводят дугу радиусом D₁ (рис. 4.4). Рассчитывают счислимое место на момент Т₁ (точка а) и уточняют его по результату измерения первого расстояния. Для этого точку а соединяют с ориентиром, а в точке К₁ пересечения этой линии с дугой радиуса D1, принимают откорректи­рованное место судна (этот перенос целесообразен только при плавании вблизи навигационных опасностей, когда линия курса после переноса оказывается смещенной в сторону опасности). По результатам прокладки рассчитывают требуемый интервал времени t между измерениями расстояний до ориентира, обеспечивающий угол пересечения навигационных изолиний болем 30. На линии пути наносят счислимую точку, соотвествующую расчетному времени измерения вторго ориентира. В момент времени , близкий к T₂ = T₁ + t, измеряют второе растояние до ориентира (D₂), фиксируя время T₂ и отсчет лага ол₂. Рассчитывают истинное расстояние D₂ = D₂+ D и из ориентира проводят дугу радиусом D₂.

По направлению пути от ориентира откладывают величину S= V(T₂— Т₁) смещения ориентира и из конца отрезка S проводят дугу радиусом D₁ до пересечения с дугой радиусом D₂. В точке пересечения дуг находится счислимо-обсервованное место судна на момент вторых наблюдений.

В судовом журнале делается следующая запись:

19.50. ол = 23,2, М_кА D₁ = 84 кбт (AD = 0,2 кбт), 20.10. ол = 26,7, М_кА D2 = 104 кбт (AD = 0,3 кбт), С= 300° - 2,3 мили.

Точность способа зависит от погрешностей в измерении расстояний, погрешностей счисления за время плавания между наблюдениями и угла между линиями положения.

4.3. Кратчайшее расстояние до ориентира по двум разновременным пеленгам на него.

Кратчайшее расстояние D_кр до ориентира рассчитывается по следующей формуле:

D_кр = К_S (4.5)

В МТ-2000 включена таблица 2.34, из которой по аргументам q и П можно выбрать величину К_.

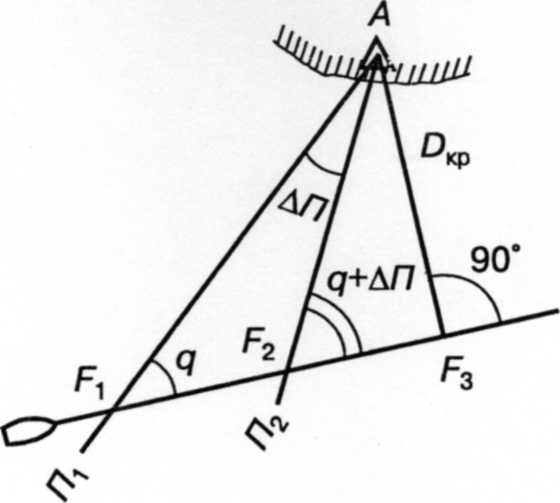
Рис. 4.5. Определение кратчайшего расстояния до ориентира.

4.4. Исправленный крюйс-пеленг

Если судно имело надежное определение по двум углам или по трем пеленгам, а затем через некоторый промежуток времени е виду его остался один предмет, пригодный для пеленгования, то для получения более точного места по крюйс-пеленгу может быть применен следующий прием, предложенный гидрографом Н.Н. Струйским и названный им «исправленный крюйс-пеленг».

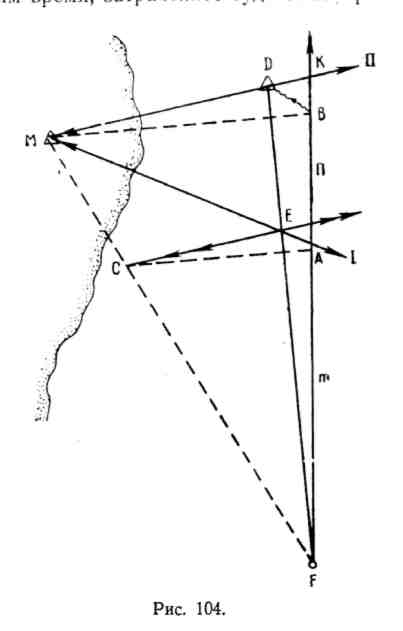
Положим, что в точке F (рис. 104) судно имело хорошее определение места по пеленгам двух или трех маяков или же по углам и, следуя дальше курсом FK, определялось по крюйс-пеленгу, имея в пределах видимости предмет М. Пусть в счислимой точке А судно взяло первый пеленг предмета М, а в счислимой точке В— второй. Обозначим время, затраченное судном на прохождение пути от обсервованной точки F до первого пеленга, через t₁, а плавание его по линии курса FA — через т; соответственно промежуток времени между пеленгами обозначим через t₂, а плавание — через п.

За промежуток времени между моментом первой обсервации судна и моментом, когда взят второй пеленг для крюйс-пеленга, равный t₁ + t₂, на судно действовало течение и ветер, вызывавшие снос судна, а погрешность лага и ошибки в поправке компаса вносили свою ошибку в счисление его пути. Если предположить, что за промежуток времени ход судна был постоянным и также принять постоянным действие различных причин, уклоняющих судно с линии его курса в течение того же промежутка времени, то перемещение судна будет прямолинейным и равномерным. При этих условиях возможно определить величину и направление сноса судна за промежуток времени t₁ + t₂, понимая под сносом суммарное действие на судно всех причин, уклоняющих его с линии курса.

Так как в момент взятия пеленгов судно должно было находиться соответственно на линии пеленгов MI и МII, то направление истинного перемещения судна при данных условиях найдется, если из точки F проведем линию пути судна FD так, чтобы отрезки ее, заключенные между точкой F и линией первого пеленга и линиями первого и второго пеленгов, относились между собой как промежутки времени t₁  t₂, затраченные на прохождение этих отрезков пути или как расстояния т: п, пройденные по счислению. Тогда будет соблюдено условие равномерности и прямолинейности перемещения судна, а также условие, что судно в заданные моменты должно находиться на линиях пеленгов, взя­тых для крюйс-пеленга.

Для графического нахождения линии пути судна соединим точку F с точкой М и разделим эту линию в отношении т: п. Это проще всего сделать, соединив точку В с точкой М и проведя прямую АС через точку А параллельно линии ВМ. Тогда

=

Проведем через полученную точку С линию второго пеленга, перенесенную параллельно, а затем соединим точку Е — пересечения линии первого пеленга с перенесенной линией второго пеленга — с точкой F и продолжим ее до пересечения с линией второго пеленга в точке D.

Полученная прямая FD и будет представлять путь судна, так как из построения видно, что эта прямая делится в точке Е в заданном отношении. Действительно

= =

Так как при построении взято отношение т: п, то если т и п получены как разности отсчетов лага, то ошибка в поправке лага не окажет влияния на конечный результат.

Определив место судна по исправленному крюйс-пеленгу в точке D и имея счислимое место в точке В, получим с прокладки отрезок BD — величину сноса за промежуток времени t₁ + t₂. Если в дальнейшем предполагается постоянство всех причин, вызывающих снос судна, то направление и скорость сноса, определенные таким путем, могут быть приняты во внимание при дальнейшей прокладке.

Чтобы сократить графическое построение в способе исправленного крюйс-пеленга, можно поступить следующим образом: от обсервованной точки F (рис. 105) прокладываем линию курса или произвольную линию FN и от точки L — пересечения этой линии с линией первого пеленга — откладываем отрезок LP = FL = FL . В полученную точку Р переносим линию первого пеленга и в точке D получаем счислимо-обсервованное место.

Прямая FD — путь судна, а его истинная скорость:

V =

В целях определения величины и направления сноса судна исправленный крюйс-пеленг может быть применен и в тех случаях, если надежное определение места судна получено через некоторый промежуток времени после определения по крюйс-пеленгу, а также в случае определения по двум разновременным пеленгам двух различных предметов.

Исследование точности этого способа, произведенное Н. Н. Струйским, и сравнение его с общим случаем крюйс-пеленга показывает, что при постоянстве направления и величины сноса исправленный крюйс-пеленг дает белее точное место, чем общий случай.

При изменении величины сноса вследствие изменения силы ветра и возбуждаемого ветром дрейфового течения исправленный крюйс-пеленг имеет преимущество во всех случаях усиливающегося течения; при значительном же ослаблении силы течения общий случай крюйс-пеленга может оказаться точнее, чем исправленный крюйс-пеленг.

При изменении направления сноса, например, в случае, если течение следует вдоль берега, изменяющего свое направление, общий случай крюйс-пеленга дает лучший результат при значительном изменении направления течения, особенно, если это изменение происходит в сторону первого пеленга. При медленном же изменении направления течения, а также если оно меняется в сторону от первого пеленга, исправленный крюйс-пеленг должен дать лучшие результаты.

В общем случае при изменении скорости и направления сноса исправленный крюйс-пеленг имеет преимущество при увеличении скорости сноса и изменении направления течения к перпендикуляру к первому пеленгу. При резком же уменьшении величины сноса и при изменении направления его в сторону первого пеленга общий случай крюйс-пеленга дает более точное определение.