4. Фактор поверхностного упрочнения

Усталостная прочность деталей во многом зависит от состояния и механических свойств поверхностных слоев металла. Для повышения прочности поверхностного слоя используются следующие технологические приемы:

- механическое упрочнение (обдув дробью; обкатка роликами);

- термическая обработка (закалка с нагревом ТВЧ; пламенная закалка);

- химико-термическая обработка [цементация; азотирование; цианирование (нитроцементация)];

C феноменологических позиций повышение предела выносливости деталей за счет поверхностного упрочнения объясняется возникновением значительных остаточных сжимающих напряжений в поверхностном слое. Повышение предела прочности деталей в этом случае происходит на 30-40%, а при наличии концентраторов напряжений – на 100%.

Влияние упрочняющей технологии на предел выносливости учитывается коэффициентом влияния поверхностного упрочнения:

; где σ_-1упр – предел выносливости упрочненных образцов; σ_-1 – предел выносливости неупрочненных образцов;

В общем случае величина К _F > 1;

5 . Фактор анизотропии

В теории сопротивления материалов принимается гипотеза об изотропности материала (т.е. однородности свойств материала в любом направлении). В действительности, например, в стальном прокате свойства материала несколько различаются в продольном и поперечном направлениям волокнам прокатки. Фактор неоднородности свойств материала в различных направлениях учитывается коэффициентом анизотропии:

; где - предел выносливости образца, вырезанного из массива проката, ориентированного в направлении проката; - предел выносливости образца, вырезанного из массива материала, в произвольном направлении;

В общем случае величина К _А < 1;

При кручении фактор анизотропии не учитывается.

О НЕКОТОРОМ РАЗЛИЧИЕ В ПОДХОДАХ К РАСЧЕТУ НА ПРОЧНОСТЬ В СОПРОМАТЕ И ДЕТАЛЯХ МАШИН

Рассмотрим диаграмму Веллера, на которой изображены две кривые: для образцов с пределом выносливости σ_-1 и для детали с пределом выносливости σ_-1Д = ; (при R = -1)

Т огда запас прочности детали можно определить из выражения: ; (*)

В СОПРОМАТЕ:

Вводится понятие эквивалентной амплитуды (материала в форме детали): и запас прочности определяется (формально) из того же выражения (*) , в котором в качестве предельного напряжения рассматривается - предел выносливости (образца);

Т.е. при данном подходе комплексный коэффициент разупрочнения К увеличивает действующие напряжения в детали.

В ДЕТАЛЯХ МАШИН:

Вводится понятие предельного напряжения детали (материала в форме детали):

и коэффициент прочности рассчитывается также по формуле (*);

Т.е. при данном подходе комплексный коэффициент разупрочнения К уменьшает предел выносливости (детали по сравнению с образцом).

РЕЗЮМЕ: указанное различие в подходах к расчету носит НЕПРИНЦИПИАЛЬНЫЙ ХАРАКТЕР и основано на исторических традициях этих двух дисциплин.

Определение предельных напряжений при произвольном коэффициенте асимметрии r

Зависимость предела выносливости образца от коэффициента асимметрии цикла R представляется графически. С этой целью по результатам усталостных испытаний строится диаграмма предельных амплитуд в координатах σ_а и σ_m, при этом средние напряжения цикла σ_m могут изменяться от отрицательных значений (сжатие) до положительных (растяжение). Любая точка поля с указанными координатами характеризует определенный цикл напряжений.

По оси абсцисс (влево от т. 0) отложены величины пределов прочности σ_вс и текучести σ_тс при сжатии и соответственно (вправо от т.0) σ_в и σ_т при растяжении. Все точки прямой А₁К, проведенной под углом 45⁰ к оси абсцисс, соответствуют циклам с максимальными напряжениями σ_мах = σ_в, а точки прямой В₁а – с напряжениями σ_мах = σ_т. Точки прямой А₂К соответствуют циклам с минимальными напряжениями σ_мin = σ_вc, а прямая В₂в – с напряжением σ_мin = σ_тc. Диаграмма предельных амплитуд обозначена А₁СА₂ и соответствует пределам выносливости при различных значениях коэффициентов асимметрии. Точка С соответствует пределу выносливости σ_-1 при R = -1, точка А₁ – пределу прочности σ_в при R = 1.

Экспериментальная диаграмма предельных амплитуд

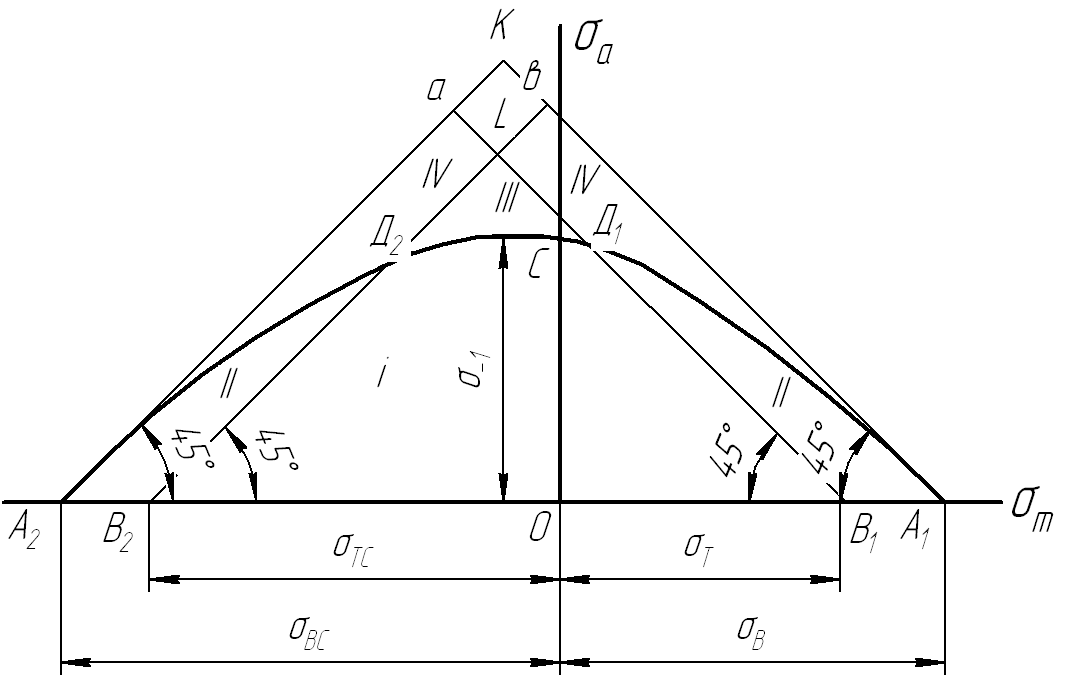
В обозначенных зонах:

Зона I – отсутствуют пластические деформации и усталостное разрушение;

Зона II - нет усталостного разрушения, но возможны пластические деформации;

Зона III – нет пластических деформаций, но возможно усталостное разрушение;

Зона IV – возможны пластические деформации и усталостное разрушение;

Усталостная прочность материалов наиболее полно изучена при цикле со средним напряжением растяжения (σ_m > 0). Поэтому за неимением достаточного объема опытных материалов в дальнейших расчетах обычно используется только правый координатный угол диаграммы. Для циклов со средним напряжением сжатия (σ_m < 0) можно воспользоваться той же диаграммой, а коэффициент асимметрии определять по формуле: , где .

Построение опытной кривой А₁С связано с известными трудностями из-за сложности экспериментального оборудования, большой длительностью испытаний и т.п. Поэтому в расчетной практике обычно используются схематизированные диаграммы, на которых отдельные участки этой кривой заменяются (аппроксимируются) прямыми линиями. При этом погрешности использования таких диаграмм идут в запас прочности.

1. Однолинейная аппроксимация.

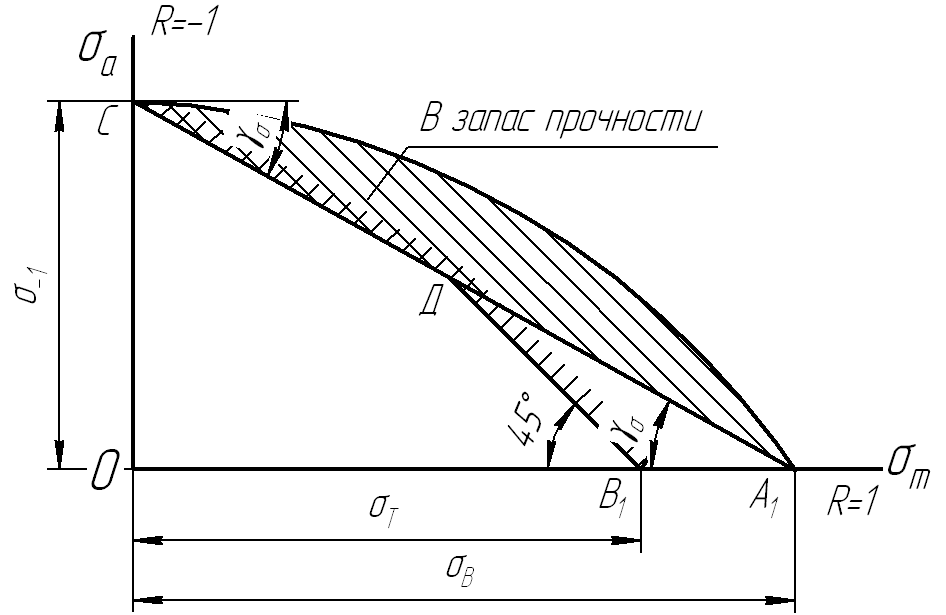
Точки на прямой СА₁ соответствуют пределам выносливости σ_R при различной асимметрии цикла . Угол ;

где - коэффициент чувствительности образца материала к асимметрии цикла;

Использование для расчетов диаграммы с однолинейной аппроксимацией сопряжено с избыточными запасами прочности. Рекомендуется использовать в интервале

2. Двухлинейная аппроксимация

Д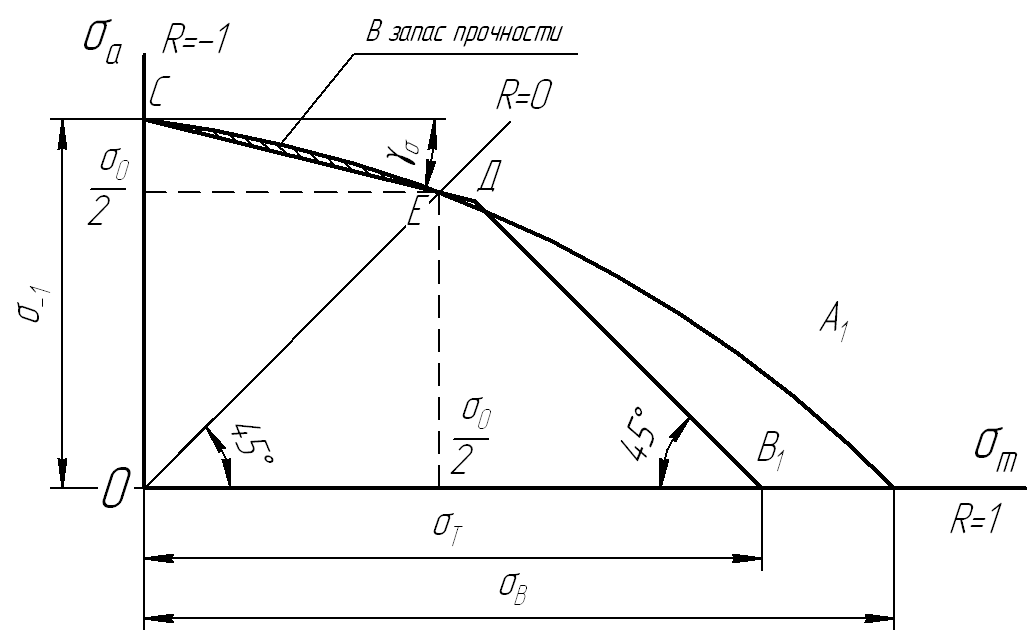 ля построения прямой СД двухлинейной диаграммы предельных напряжений используются две усталостных характеристики материала: σ_-1 и σ₀, где σ₀ – предел выносливости при отнулевом (пульсирующем) цикле при R = 0 (в этом случае - запас – уменьшается). [Ориентировочные значения пределов выносливости при R = 0 можно определить из выражений: - при изгибе; и - при сдвиге];

Численное значение коэффициента чувствительности (для образца) определяется в этом случае по эмпирической формуле: ; ;

Величина этого коэффициента зависит от материала и вида деформации.

Точки на отрезке СЕ соответствуют пределам выносливости σ_R при различной асимметрии цикла на интервале , в котором и рекомендуется использовать.

Прямые ВД на обеих диаграммах, проведенные из точки σ_m = σ_Т под углом 45⁰ к оси, ограничивают область возможных циклов условием σ_mах < σ_T (ограничивая, тем, самым, появление пластических деформаций).

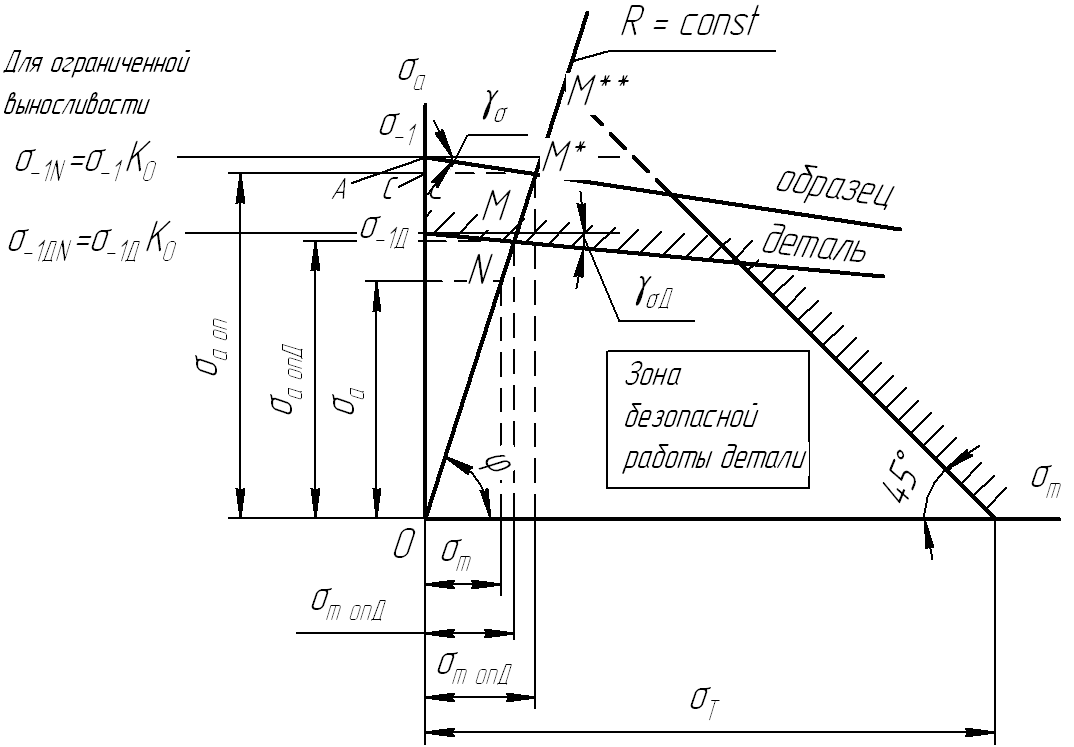
Определение предельных напряжений (образца и детали) при произвольном коэффициенте асимметрии σ_R. (см. рисунок)

ОС = ВМ = АО – АС;

σ_оп = σ_R = σ_аоп + σ_mоп ; Для выражения σ_аоп можно использовать уравнение прямой с угловым коэффициентом (типа у = кх + b, где к = tgα): σ_аоп = σ_-1 – σ_mtg γ_σ; (*)

Учитывая (из ранее сказанного) и , а также, что предельные напряжения σ_R – являются максимальными напряжениями цикла, имеем и ; Тогда, подставляя в (*): , и с учетом получаем искомое выражение: - предельные напряжения для материала в форме образца.

Предельные напряжения для детали можно определить как

;

где и - коэффициент чувствительности материала в форме детали к асимметрии цикла; К – комплексный коэффициент разупрочнения детали (по сравнению с образцом).

Если действительное число циклов меньше базового (N_i < N₀), то в качестве предельного напряжения материала детали рассматривается предел ограниченной выносливости материала (в форме детали) при произвольном коэффициенте асимметрии R:

; К₀ - коэффициент долговечности;

или (а) – по Комкову В.Н.

Отдельные авторы (например, Кудрявцев В.Н., [4]) полагают, что коэффициент долговечности (фактор времени) К₀ должен относится только к амплитудному напряжению и предлагают выражение для определения σ_RДN использовать в виде:

(б) – по Кудрявцеву В.Н.

Следует отметить, что численное расхождение результатов расчетов по (а) и (б) составляет доли процента, поэтому в расчетной практике их можно рассматривать равноценными.

Расчетный коэффициент запаса определяется: ;

или с учетом и : ;

Точка N на диаграмме соответствует действующим (максимальным) напряжениям детали σ_мах. Точка М – предельным напряжениям материала (в форме детали) – σ_RД (или σ_{RД N} – при ограниченной выносливости).

По диаграмме можно графически определить коэффициент запаса:

- усталостной (циклической ) прочности детали:

;

- статической прочности детали:

;

П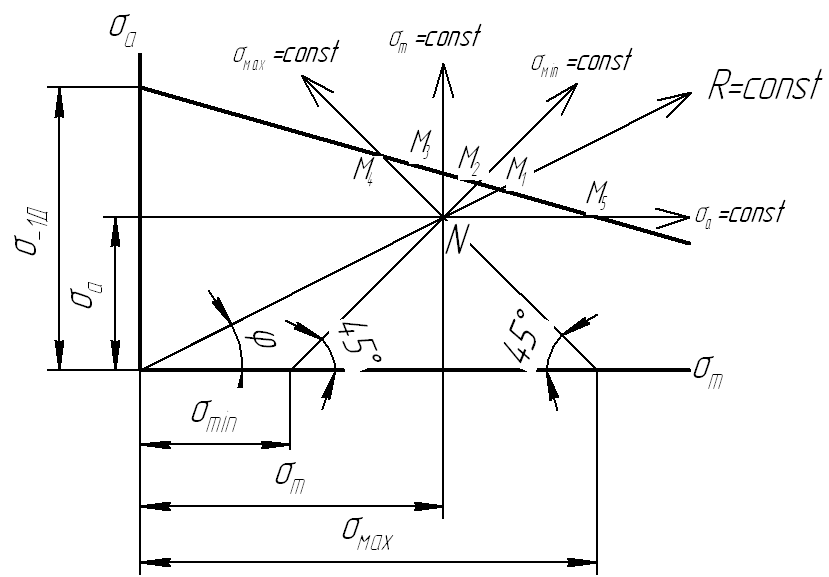 ереход детали от рабочего состояния (т.N) к предельному (т.М) может происходить по различным законам:

Нагружение детали при R = const называется простым нагружением (ось, нагруженная постоянной по направлению силой); Если при переходе детали к предельному состоянию асимметрия цикла изменяется, нагружение называется сложным.

Нагружение при σ_min = const имеет место в напряженном болтовом соединении при действии внешней пульсирующей нагрузки.

Нагружение при σ_m = const характерно для напряженного клинового соединения;