Ременные передачи

О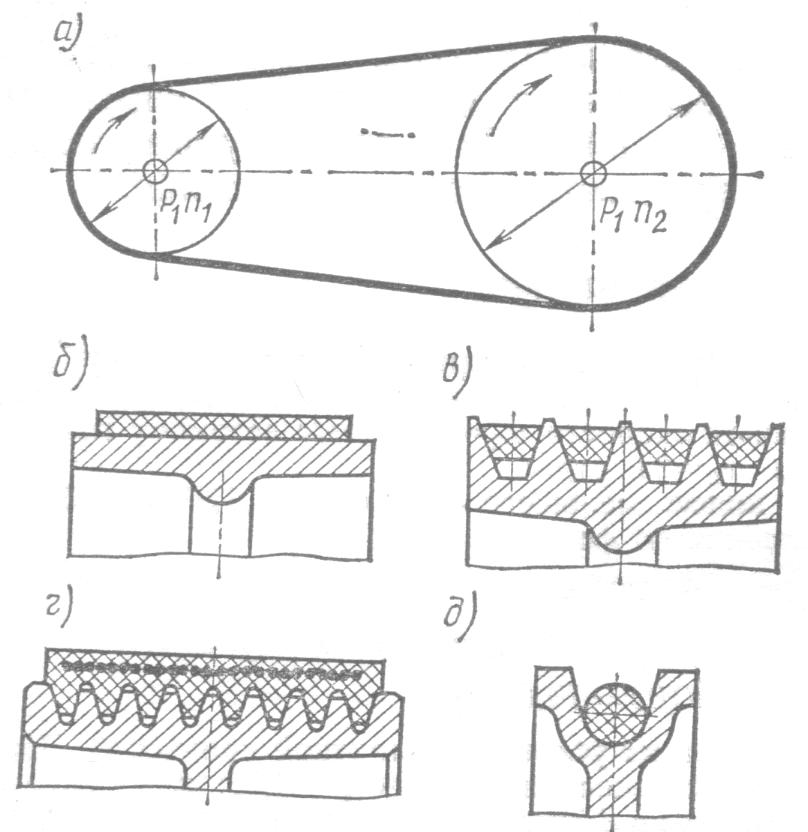 тносятся к передачам работающих за счет трения

1 2

3

Конструкция РП включает: ведущий и ведомый шкивы, и ремень - гибкая связь;

Достоинства РП:

- простота изготовления, относительная дешевизна;

- возможность передачи вращения на большие расстояния (до 15 м и более) – для плоскоременных передач;

- бесшумность и плавность работы;

- могут использоваться в механизмах в качестве предохранительного устройства;

Недостатки РП:

- большие габариты;

- непостоянство передаточного отношения (зависит от нагрузки), целесообразно применять в силовых приводах;

- значительные нагрузки на соединяемые валы;

Классификация рп

1. По типу ремней

- плоскоременные:

- клиноременные:

- с поликлиновым ремнем:

- с круглым ремнем:

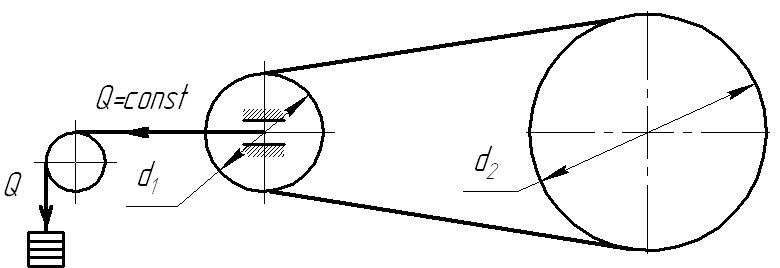
2. По принципу натяжения ремней

- автоматическое натяжение:

(Q = const)

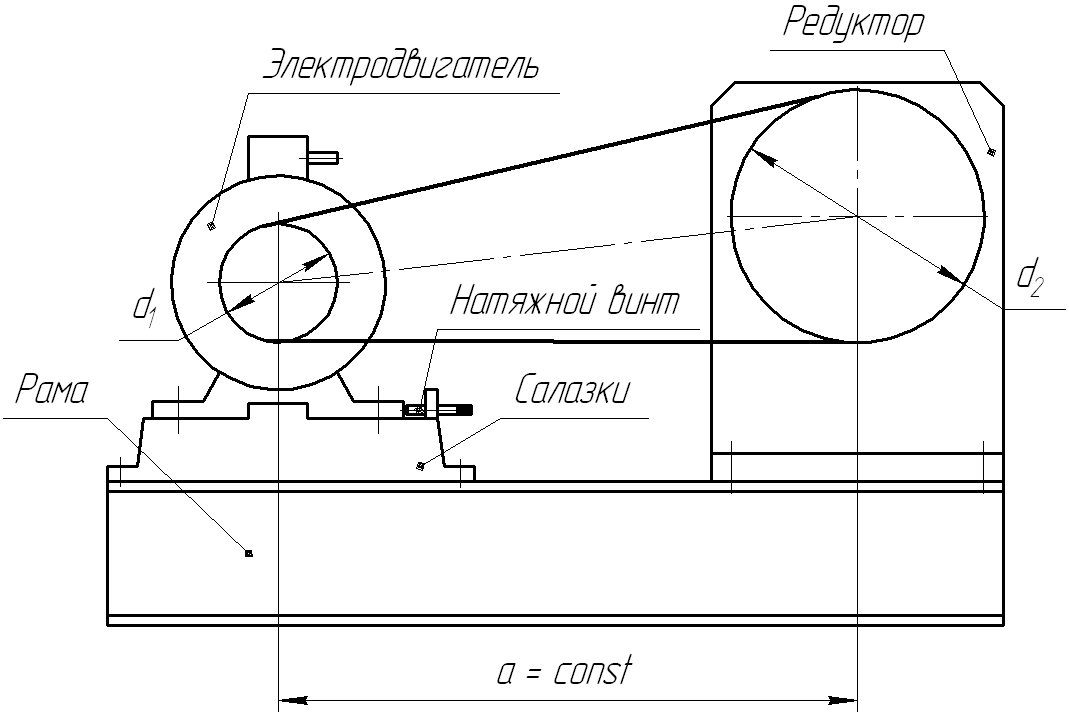
- периодическое натяжение:

(a = const)

Соотношение сил в ветвях ременной передачи

(из основ теории трения гибких нитей по Л.Эйлеру)

Известно: F₂, f, α; Определить: F₂

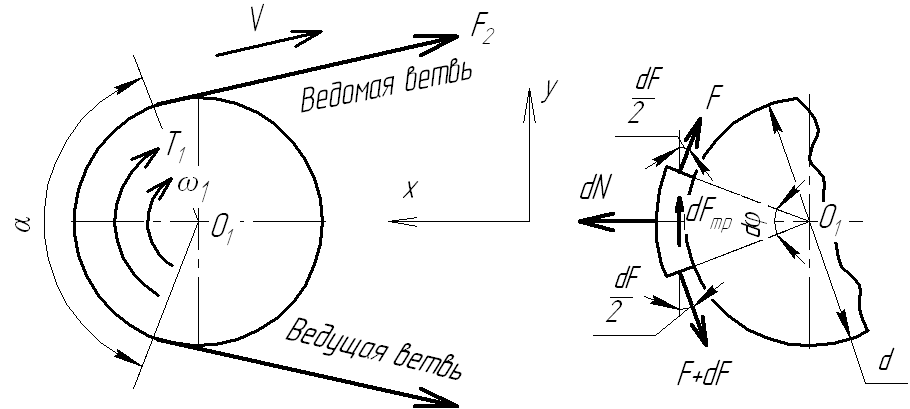
1. Уравнение равновесия (по моментам):

откуда

(1)

2. Проекция сил на ось Х:

С учетом: (для малых углов) и (как б.м.в. 2-го порядка), имеем: в итоге получаем систему:

1)

2)

Из которой, после подстановки, имеем: ;

Разделяем переменные: и интегрируем по углу охвата:

; или

Окончательно: - уравнение Эйлера;

Рассмотрим 2 частных случая

1) Передача не работает: [V (окружная скорость ремня) = 0; T (передаваемый момент) = 0];

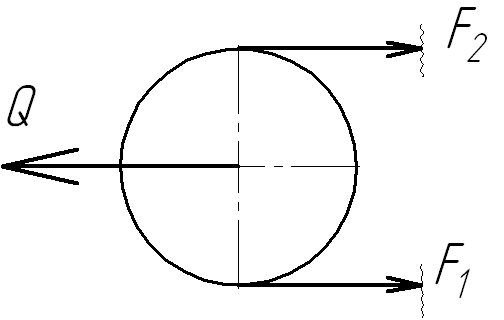
F₁ = F₂ = F₀ - усилие предварительного натяжения ветвей ремня;

Из условия равновесия ремня:

Q = 2F₀ – усилие натяжения ремня (равно нагрузке, действующей на валы);

2. Передача работает на холостом ходу: ( );

При прохождении ремнем шкивов (и его изгибе) появляются центробежные силы

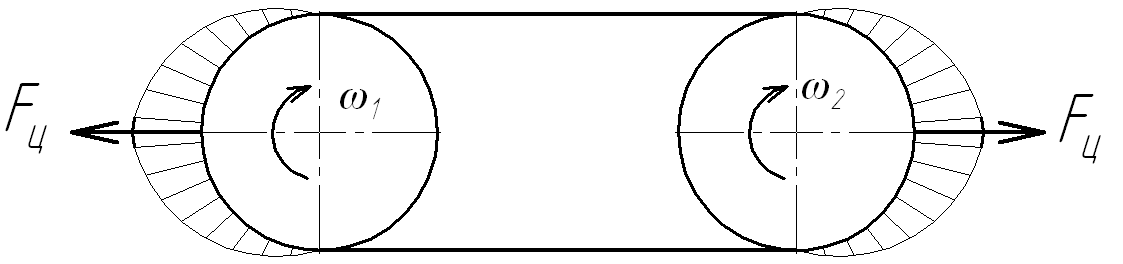
Оценим их величину.

Известно: V (м/с) – окружная скорость ремня; ρ (кг/м³) – плотность ремня; А – площадь поперечного сечения ремня;

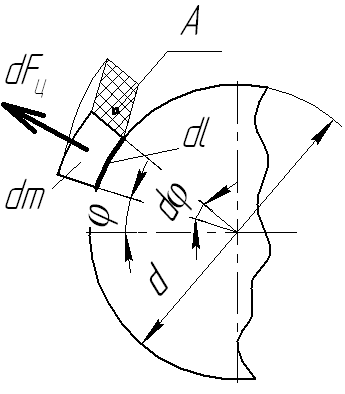
φ –угол охвата; dm – элементарная масса; dF_ц – элементарная центробежная сила;

Центробежная сила в общем виде: F_ц = m∙r∙ω²;

;

(*)

где

Интегрируя выражение (*), получим:

Влияние центробежных сил проявляется при окружных скоростях V ≥ 15…20 м/с

Рассмотрим различные варианты натяжения ремня:

а) Автоматическое натяжение: Q = 2F₀ = const;

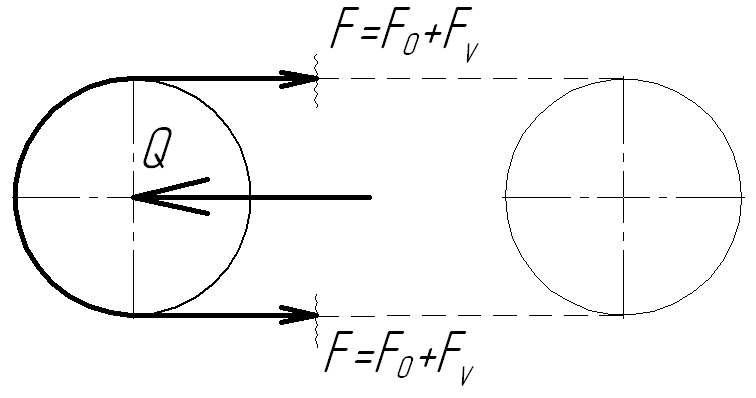
F_ц + Q -2F = 0 или F_ц + 2F₀ -2F = 0, откуда

F = F₀ + = F₀ + F_v; где

В этом случае происходит постоянный контакт ремня со шкивом, и центробежная сила распределяется между ветвями ремня.

б) Периодическое натяжение: а = const;

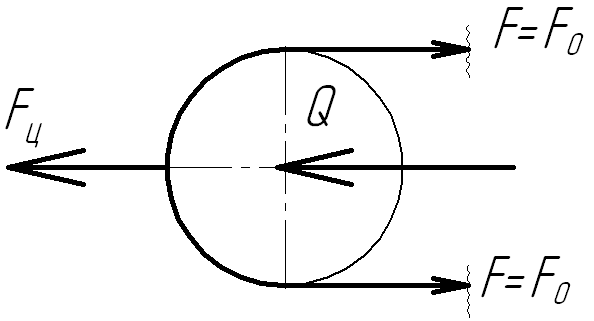
F_ц +Q - 2F =0;

При постоянном межосевом расстоянии общая длина ремня не меняется, т.е. Δl = 0 (и ε = 0), и, следовательно, напряжения в ремне не меняются, т.е. F = F₀, или F + Q – 2F₀ = 0, откуда Q = 2F₀ - F_ц;

В этом случае центробежная сила ослабляет контакт ремня и шкива, и уменьшая трение между ними, снижает тяговую способность передачи.

Аналогом может служить напряженное резьбовое соединение: F = F₀ + χF_ц

- при автоматическом натяжении: χ = 1 (центробежная сила передается на ремень);

- при периодическом натяжении: χ = 0 (центробежная сила ослабляет контакт ремня и шкива);

М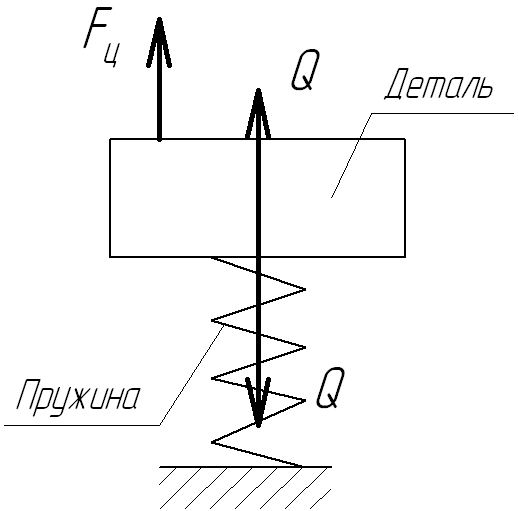 ожно также проиллюстрировать на примере модели:

Пока под действием силы F_ц не произойдет отрыва детали, усилие Q в пружине не изменится.

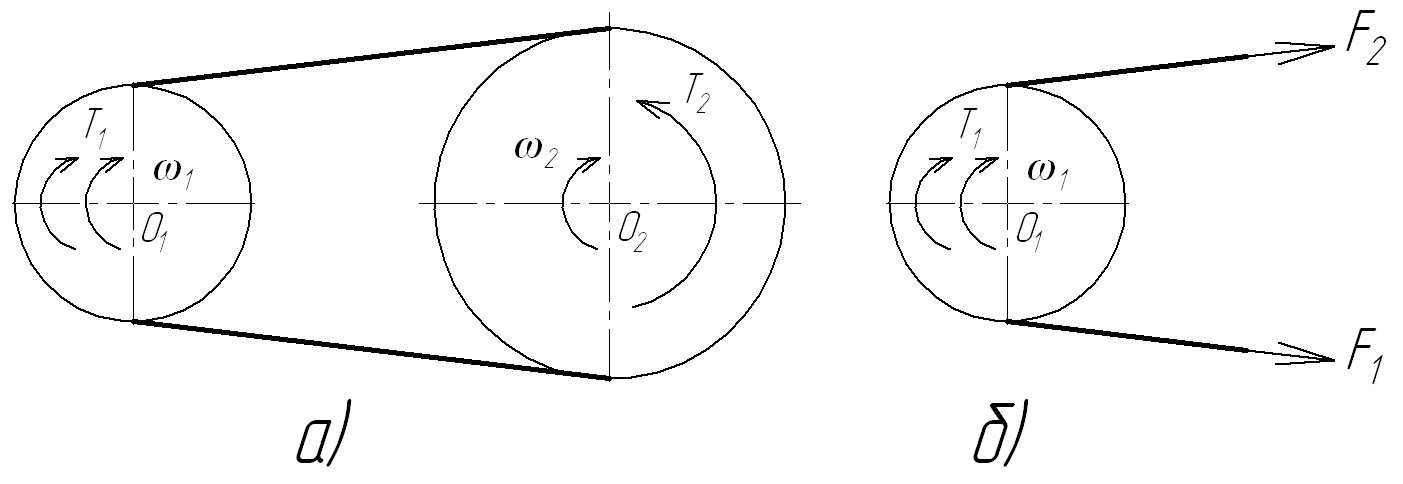
3) РП в рабочем состоянии (Т ≠ 0, ω ≠ 0) - см. рис.а);

(см рис.б)

F₁ – F₂ = = F_t – окружная сила РП (тяговая способность)

Решая систему из двух уравнений:

F₁ + F₂ = 2F₀ = const; (1) получаем: ;

F₁ – F₂ = F_t ; (2) ;

Или, с учетом выражения , имеем

- при автоматическом натяжении:

;

;

Уравнение Эйлера с учетом центробежных сил:

;

- мах тяговая способность

- при периодическом натяжении:

(если то ; если то )