26

Производная и дифференциал 1

Понятие производной 1

Геометрический смысл производной 1

Физический и экономический смысл производной 2

Дифференцируемость функции 4

Схема вычисления производной 5

Основные правила дифференцирования 5

Производные основных элементарных функций 7

Производные высших порядков 8

Эластичность функции 8

Основные теоремы о дифференцируемых функциях и их приложения 9

Экстремумы функции 14

Выпуклость функции 17

Асимптоты графика функции 20

Дифференциал функции 22

Применение дифференциала в приближенных вычислениях 24

Понятие о дифференциалах высших порядков 26

Производная и дифференциал Понятие производной

Пусть функция у = f(x) определена на промежутке X. Возьмем точку х  Х. Дадим значению х приращение х  0, тогда функция получит приращение  у = f(x + х) - f(x).

Производной функции у = f(x) называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю (если этот предел существует): .

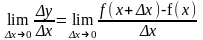Производную также обозначают y' и dy/dx.

Геометрический смысл производной

Чтобы понять геометрический смысл производной, рассмотрим задачу о касательной.

Рассмотрим на плоскости график непрерывной функции у = f(x) (см. рисунок 3.1).

Построим касательную к этой кривой в точке М₀(х₀, у₀). Прежде всего, необходимо определить понятие касательной. Для этого дадим аргументу х₀ приращение х и перейдем на кривой у = f(x) от точки М₀(х₀, f(x₀)) к точке М₁(х₀ + х, f(х₀ + х)). Проведем секущую М₀М₁. Под касательной к кривой у = f(x) понимают предельное положение секущей М₀М₁ при приближении точки М₁ к точке М₀, т.е. при х0.

Угловой коэффициент секущей М₀М₁ (тангенс угла  наклона этой прямой к оси абсцисс) может быть найден из М₀М₁N: . Тогда угловой коэффициент касательной (тангенс угла ) равен .

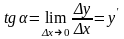Таким образом, производная функции представляет собой тангенс угла наклона касательной к графику функции к оси абсцисс (угловой коэффициент касательной).

Физический и экономический смысл производной

Рассмотрим прямолинейное движение по закону s=s(t), где s - пройденный путь, а t – время. Необходимо найти скорость движения v в момент t₀.

За промежуток времени t с момента t₀ будет пройдено расстояние s = s(t₀ + t) - s(t₀). Тогда средняя скорость за этот промежуток времени составит s/t. Чем меньше будет промежуток t, тем лучше это отношение будет оценивать скорость в момент времени t₀: .

Таким образом, производная функции представляет собой скорость изменения значения функции в точке. Этот смысл производной удобно использовать не только в физике, но и в экономике.

Например, если функция p = p(q) выражает зависимость прибыли p от объема произведенной продукции q, то ее производная показывает предельный рост прибыли (скорость изменения прибыли при изменении объема производства): 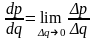. Если функция q = q(u) выражает зависимость объема производства q от числа работников u, то ее производная показывает скорость изменения этого объема при изменении числа работников: 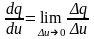(предельная производительность дополнительного работника). Если функция описывает зависимость объема производства от времени, то получим производительность в единицу времени. 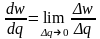Если функция w = w(q) выражает зависимость издержек производства от количества выпускаемой продукции, то ее производная означает предельные издержки (приближенно показывает дополнительные затраты на производство единицы дополнительной продукции): И т.п.

На основе понятия производной в экономике рассчитываются предельная выручка, предельный доход, предельный продукт, предельная полезность, предельная производительность и другие предельные величины.

Предельные величины характеризуют процесс изменения экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) во времени или относительного другого исследуемого фактора.